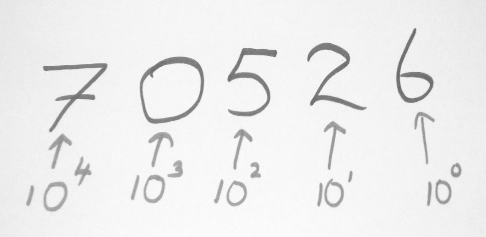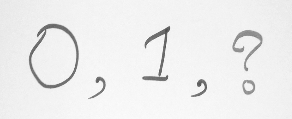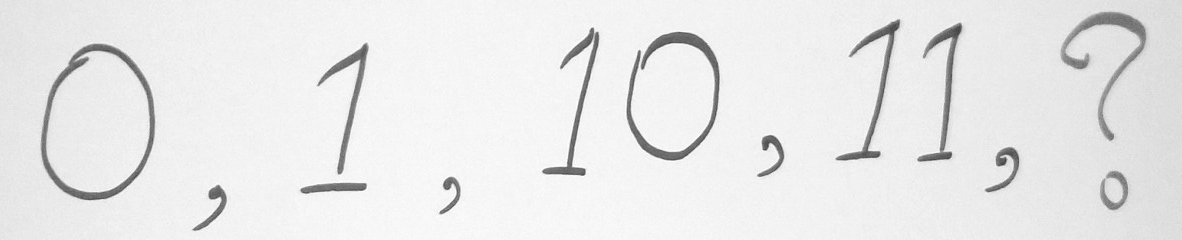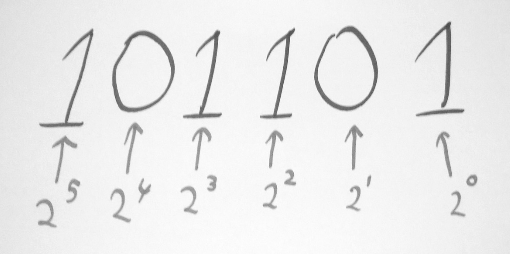A symbol that is not used in the decimal system
A symbol that is not used in the decimal system
Number Systems — Decimal, Binary, Octal and Hexadecimal
Let’s explore few different number systems that are in use today and see how with simple three rules, we can build any number system we want.
In mathematics, a “base” or a “radix” is the number of different digits or combination of digits and letters that a system of counting uses to represent numbers.
In any of the number systems mentioned above, zero is very important as a place-holding value. Take the number 1005. How do we write that number so that we know that there are no tens and hundreds in the number? We can’t write it as 15 because that’s a different number and how do we write a million (1,000,000) or a billion (1,000,000,000) without zeros? Do you realize it’s significance?
First, we will see how the decimal number system is been built, and then we will use the same rules on the other number systems as well.
So how do we build a number system?
We all know how to write numbers up to 9, don’t we? What then? Well, it’s simple really. When you have used up all of your symbols, what you do is,
If you use the above 3 rules on a decimal system,
So you see when we have ten different symbols, when we add digits to the left side of a number, each position is going to worth 10 times more than it’s previous one.
How to read numbers?
Let’s take the same decimal number system. There are only two rules actually.
Let’s take one digit number ‘8’. This simply means 8, in other words, it is exactly what it says it represents. What about 24? In case of two digits, right digit says what it means, but left digit means ten times what it says. That is, 4 is 4, 2 is 20. Altogether forms 24.
If we take a three digit number, rightmost digit means what it says, the middle one is ten times what it says, leftmost digit 100 times what it says. Simply if we take number 546, it means 6 + (10 * 4) + (5 * 100) = 546.
Binary
With binary, we have only two digits to represent a number, 0 and 1 and we are already out of symbols. So what do we do? Let’s apply the same rules that we used on the decimal system.
We make the right digit 0 and add 1 to left, that is, our next number is ‘10’. Then we go up until we used up all our symbols on the right side.So the next number in line is 11.
After ‘11’, we put 0s in both these places and add 1 to the left and we get 100.
Then 101, 110, 111 then 1000 …
This binary number system is based on two digits and each position is worth two times more than the previous position.
Reading a binary number is almost same as reading a decimal. Right digit says what it means, next one means two times the previous one, after that 4 times etc…
So 101 means 5 in decimal.
These same rules apply to octal and hexadecimal number systems as well. With octal, we have only 8 digits to represent numbers so once we get to 7 the next number is 10 and in hexadecimal, we have 10 digits and 6 letters to represent numbers. In that case, when we reach 9 next number is represented in the letter ‘A’. Next one ‘B’. Likewise, we go up to letter ‘F’ and after ‘F’ comes ‘10’.
I’ll just list down few numbers in these 4 different number systems and see whether you can apply the rules that we discussed above to get the next number.
To understand how computers represent positive and negative numbers, please read this and more on hexadecimal can be found here.
How to change decimal symbol and digit grouping symbol in Windows 10
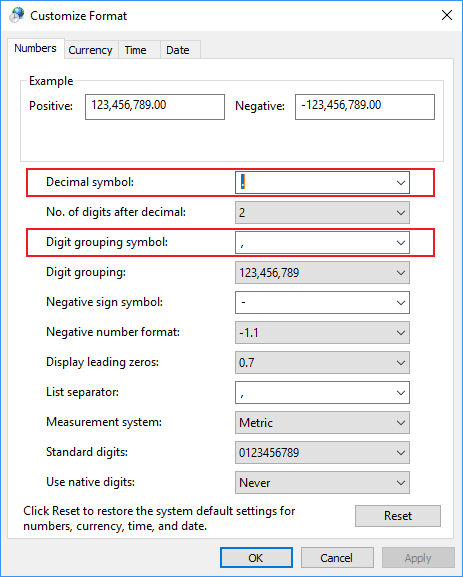
A decimal symbol or decimal separator is a symbol used to separate the integer part from the fractional part of a number written in decimal form. This symbol can be a period or a comma.
For ease of reading, numbers with many digits may be divided into groups using a digit grouping symbol, such as comma, dot, space, etc.
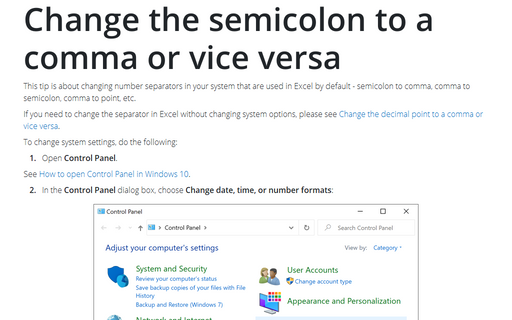
To see or change pre-defined in Windows 10 decimal symbol and digit grouping symbol, do the following:
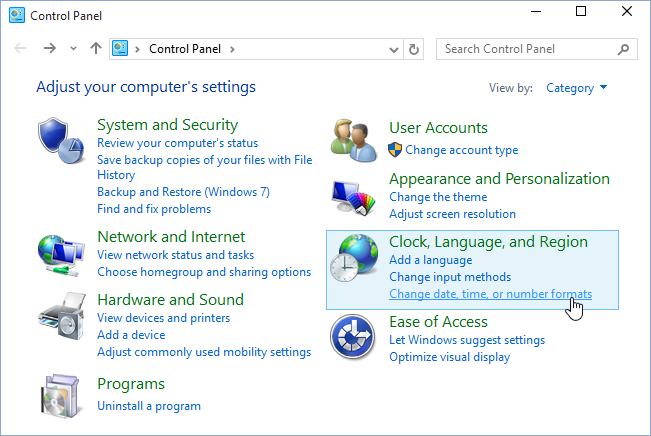
1. Open Control Panel.
2. In the Control Panel dialog box, hoose Change date, time, or number formats:
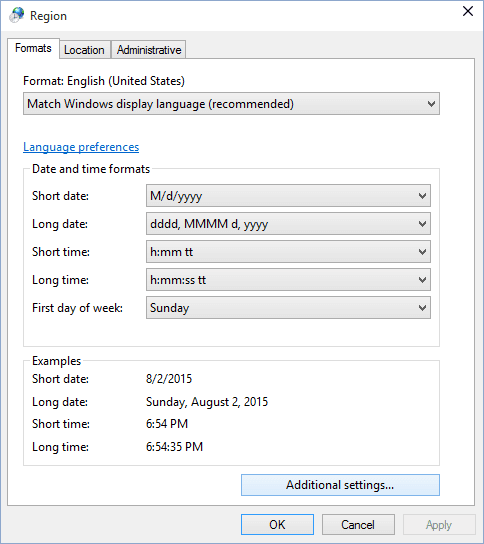
3. In the Region dialog box, choose Additional settings. :
4. In the Customize Format dialog box, choose appropriate value from the list Decimal symbol and/or Digit grouping symbol, or enter the new one:
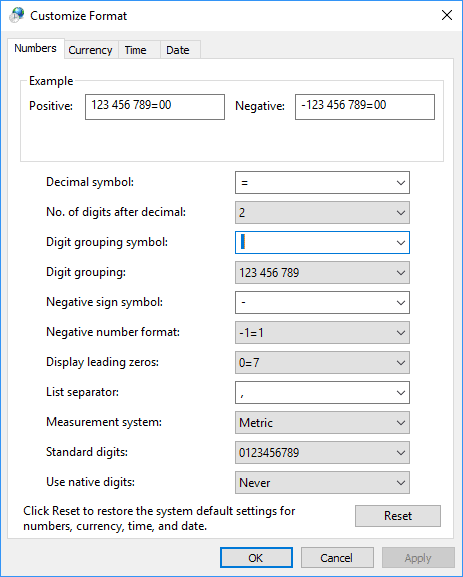
5. After clicking the Apply button, you can see how Windows will show amounts in the Example group in the bottom of the dialog box:
Change the semicolon to a comma or vice versa
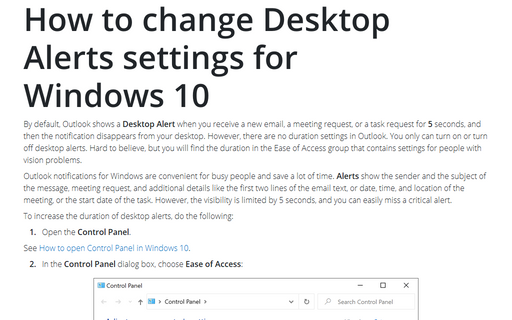
How to change Desktop Alerts settings for Windows 10
How to open Control Panel in Windows 10
We use cookies to personalise content and ads, to provide social media features and to analyse our traffic. We also share information about your use of our site with our social media, advertising and analytics partners who may combine it with other information you’ve provided to them or they’ve collected from your use of their services.
Decimal system
The decimal numbering system is also known as a decimal system and consists of a positional numbering system. This positional system is a set of symbols and rules that allow us to form all the numbers that exist and that are valid. In the decimal system, quantities can be represented using arithmetic bases, ten powers. The Arabic or Indo-Arabic numbers are the symbols used to represent the decimal system and it is composed of ten different digits: zero (0), one (1), two (2), three (3), four (4), five (5), six (6), seven (7), eight (8), nine (9). This system is used worldwide and in all mathematical aspects.
Related Topics
What is the decimal system?
The decimal system is a numbering system composed of a series of symbols that, respecting different rules, are used to build the different valid numbers taking into account the ten base. It is the way to represent quantities using ten digits from 0 to 9.
What is the decimal system for?
The decimal system is a necessary system in our daily lives. Most of the things we do are surrounded by numbers and it is necessary to have a way of expressing them in order to perform different activities, measure an object, perform different calculations, pay the bill in a store or restaurant. The decimal system allows us to construct all the numbers that are valid in the system. It is a way of counting numbers. This system is a way that humanity has accepted to count. Another important function of this system is that it helps us to communicate, because it helps us to represent things and large quantities, since numbers that are too large could not be easily represented.
Characteristics
History
From very ancient times, civilizations used different types of numbering systems to represent numbers. Some of them, like the Roman or the sexagesimal systems that were used in ancient Babylon, can still be observed today in our society, being the case, for example, when we use Roman numerals to represent centuries or years, or time, when we write it as 18:56. According to studies conducted by different anthropologists, the origin of this system is in hand fingers, which have been used for centuries to count. The development of numbers 1 to 9 originated in India, according to what was rescued from the Inscriptions of Nana Ghat, which date from the 3rd century BC. Sometime later, the Arabs began to use the numbers we know today.
Who invented the decimal system
This numerical system was created by Hindu peoples. Sometime after this system was created in India, the astronomer, mathematician and geographer Al-Khwarizmi, who was born in Persia in the year 780, introduced the decimal numbering system that is currently used all over the world. Al-Khwarizmi studied for a long time this system and the correct way to use it to make calculations with it. He perfected it with his own contributions and looked for a way to be able to use zero as a number. Thanks to his work, the system was translated into Latin and managed to be included in Europe, where it was decided to abandon the Roman numbering system and adopt the decimal numbering system. Today, the system is used all over the world and, because it came to Europe through the Arabs and the works of Al-Khwarizmi, it is also known as the Arabic numbering system.
Decimal system symbols
The symbols used by decimal system are the numbers from 0 to 9, and each of these numbers is associated with a certain value that depends on its position, the further to the left the number is, its number will be ten times more than it is worth. As such, in a natural number we can find the following figures:
A symbol that is not used in the decimal system
Each symbol represents a unique value. You are familiar with the decimal system, using the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The decimal system is based on the powers of 10.When we want to represent a value greater than 9, we use a compound system, where the right-most symbol is one power of ten lower that its neighbor on the left.
Decimal System
These are mathematical concepts we use daily, even if we do not think about them when we use those concepts.
Binary System
The most common powers of two and values (which are the ones you are expected to know) are:
| 2 0 | 1 |
| 2 1 | 2 |
| 2 2 | 4 |
| 2 3 | 8 |
| 2 4 | 16 |
| 2 5 | 32 |
| 2 6 | 64 |
| 2 7 | 128 |
| 2 8 | 256 |
| 2 9 | 512 |
| 2 10 | 1024 |
| 2 11 | 2048 |
| 2 12 | 4096 |
| 2 13 | 8192 |
| 2 14 | 16384 |
| 2 15 | 32768 |
| 2 16 | 65536 |
To convert a binary number to decimal, simply add up the decimal equivalents of the positions in the value that are non-zero This leads to 10112 being converted as:
Examination of this example should reveal that we used the same concepts, but substituted two for ten as the base.
To convert a decimal number to binary, we can use subtraction to reverse the process. (Note: There are other methods, but this only involves adding and subtractings.)
Now subtract 128 from 240.
And Continuing
Well, 64 can be subtracted, so: 32 can be subtracted, so: 16 can be subtracted, so: 8 can not be subtracted, so: 4 can not be subtracted, so: 2 can not be subtracted, so: 1 can not be subtracted, so:
Hexadecimal System
This leads to FE08: We can compare the first sixteen binary, decimal, and hexadecimal values in the following table:
| Binary | Decimal | Hex |
|---|---|---|
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
One of the things to note, the value 0000 is exactly the same value as 0. Leading zeroes do not alter a value. When working with binary and hex values, it is common to write them as 8-, 16-, or 32-bit values by adding the necessary leading zeroes.
Unicode Locale Data Markup Language (LDML)
Part 3: Numbers
For the full header, summary, and status, see Part 1: Core.
Summary
This document describes parts of an XML format (vocabulary) for the exchange of structured locale data. This format is used in the Unicode Common Locale Data Repository.
This is a partial document, describing only those parts of the LDML that are relevant for number and currency formatting. For the other parts of the LDML see the main LDML document and the links above.
Status
This document has been reviewed by Unicode members and other interested parties, and has been approved for publication by the Unicode Consortium. This is a stable document and may be used as reference material or cited as a normative reference by other specifications.
A Unicode Technical Standard (UTS) is an independent specification. Conformance to the Unicode Standard does not imply conformance to any UTS.
Please submit corrigenda and other comments with the CLDR bug reporting form [Bugs]. Related information that is useful in understanding this document is found in the References. For the latest version of the Unicode Standard see [Unicode]. For a list of current Unicode Technical Reports see [Reports]. For more information about versions of the Unicode Standard, see [Versions].
Parts
The LDML specification is divided into the following parts:
Contents of Part 3, Numbers
1 Numbering Systems
Numbering systems information is used to define different representations for numeric values to an end user. Numbering systems are defined in CLDR as one of two different types: algorithmic and numeric. Numeric systems are simply a decimal based system that uses a predefined set of digits to represent numbers. Examples are Western ( ASCII digits ), Thai digits, Devanagari digits. Algorithmic systems are more complex in nature, since the proper formatting and presentation of a numeric quantity is based on some algorithm or set of rules. Examples are Chinese numerals, Hebrew numerals, or Roman numerals. In CLDR, the rules for presentation of numbers in an algorithmic system are defined using the RBNF syntax described in Section 6: Rule-Based Number Formatting.
Attributes for the element are as follows:
For general information about the numbering system data, including the BCP47 identifiers, see the main document Section Q.1.1 Numbering System Data.
2 Number Elements
2.1 Default Numbering System
This element indicates which numbering system should be used for presentation of numeric quantities in the given locale.
2.2 Other Numbering Systems
This element defines general categories of numbering systems that are sometimes used in the given locale for formatting numeric quantities. These additional numbering systems are often used in very specific contexts, such as in calendars or for financial purposes. There are currently three defined categories, as follows:
native
traditional
Defines the traditional numerals for a locale. This numbering system may be numeric or algorithmic. If the traditional numbering system is not defined, applications should use the native numbering system as a fallback.
finance
Defines the numbering system used for financial quantities. This numbering system may be numeric or algorithmic. This is often used for ideographic languages such as Chinese, where it would be easy to alter an amount represented in the default numbering system simply by adding additional strokes. If the financial numbering system is not specified, applications should use the default numbering system as a fallback.
The categories defined for other numbering systems can be used in a Unicode locale identifier to select the proper numbering system without having to know the specific numbering system by name. For example:
For more information on numbering systems and their definitions, see Section 1: Numbering Systems.
2.3 Number Symbols
Number symbols define the localized symbols that are commonly used when formatting numbers in a given locale. These symbols can be referenced using a number formatting pattern as defined in Section 3: Number Format Patterns.
The available number symbols are as follows:
decimal
separates the integer and fractional part of the number.
group
separates clusters of integer digits to make large numbers more legible; commonly used for thousands (grouping size 3, e.g. «100,000,000») or in some locales, ten-thousands (grouping size 4, e.g. «1,0000,0000»). There may be two different grouping sizes: The primary grouping size used for the least significant integer group, and the secondary grouping size used for more significant groups; these are not the same in all locales (e.g. «12,34,56,789»). If a pattern contains multiple grouping separators, the interval between the last one and the end of the integer defines the primary grouping size, and the interval between the last two defines the secondary grouping size. All others are ignored, so «#,##,###,####» == «###,###,####» == «##,#,###,####».
list
symbol used to separate numbers in a list intended to represent structured data such as an array; must be different from the decimal value. This list separator is for “non-linguistic” usage as opposed to the listPatterns for “linguistic” lists (e.g. “Bob, Carol, and Ted”) described in Part 2, Section 11 List Patterns.
percentSign
symbol used to indicate a percentage (1/100th) amount. (If present, the value is also multiplied by 100 before formatting. That way 1.23 → 123%)
nativeZeroDigit
patternDigit
Deprecated. This was formerly used to provide the localized pattern character corresponding to ‘#’, but localization of the pattern characters themselves has been deprecated for some time (determining the locale-specific replacements for pattern characters is of course not deprecated and is part of normal number formatting).
minusSign
Symbol used to denote negative value.
plusSign
Symbol used to denote positive value. It can be used to produce modified patterns, so that 3.12 is formatted as «+3.12″, for example. The standard number patterns (except for type=»accounting») will contain the minusSign, explicitly or implicitly. In the explicit pattern, the value of the plusSign can be substituted for the value of the minusSign to produce a pattern that has an explicit plus sign.
approximatelySign
Symbol used to denote a value that is approximate but not exact. The symbol is substituted in place of the minusSign using the same semantics as plusSign substitution.
exponential
Symbol separating the mantissa and exponent values.
superscriptingExponent
perMille
symbol used to indicate a per-mille (1/1000th) amount. (If present, the value is also multiplied by 1000 before formatting. That way 1.23 → 1230 [1/000])
infinity
The infinity sign. Corresponds to the IEEE infinity bit pattern.
The NaN sign. Corresponds to the IEEE NaN bit pattern.
currencyDecimal
Optional. If specified, then for currency formatting/parsing this is used as the decimal separator instead of using the regular decimal separator; otherwise, the regular decimal separator is used.
currencyGroup
Optional. If specified, then for currency formatting/parsing this is used as the group separator instead of using the regular group separator; otherwise, the regular group separator is used.
timeSeparator
Note: In CLDR 26 the timeSeparator pattern character was specified to be COLON. This was withdrawn in CLDR 28 due to backward compatibility issues, and no timeSeparator pattern character is currently defined. No CLDR locales are known to have a need to specify timeSeparator symbols that depend on number system; if this changes in the future a different timeSeparator pattern character will be defined. In the meantime, since CLDR data consumers can still request the timeSeparator symbol. it should match the symbol actually used in the timeFormats and availableFormats items.
The numberSystem attribute is used to specify that the given number symbols are to be used when the given numbering system is active. Number symbols can only be defined for numbering systems of the «numeric» type, since any special symbols required for an algorithmic numbering system should be specified by the RBNF formatting rules used for that numbering system. By default, number symbols without a specific numberSystem attribute are assumed to be used for the «latn» numbering system, which is western (ASCII) digits. Locales that specify a numbering system other than «latn» as the default should also specify number formatting symbols that are appropriate for use within the context of the given numbering system. For example, a locale that uses the Arabic-Indic digits as its default would likely use an Arabic comma for the grouping separator rather than the ASCII comma. For more information on numbering systems and their definitions, see Section 1: Numbering Systems.
2.4 Number Formats
(scientificFormats, percentFormats have the same structure)
Number formats are used to define the rules for formatting numeric quantities using the pattern syntax described in Section 3: Number Format Patterns.
Different formats are provided for different contexts, as follows:
decimalFormats
The normal locale specific way to write a base 10 number. Variations of the decimalFormat pattern are provided that allow compact number formatting.
percentFormats
Pattern for use with percentage formatting
scientificFormats
Pattern for use with scientific (exponent) formatting.
The numberSystem attribute is used to specify that the given number formatting pattern(s) are to be used when the given numbering system is active. By default, number formatting patterns without a specific numberSystem attribute are assumed to be used for the «latn» numbering system, which is western (ASCII) digits. Locales that specify a numbering system other than «latn» as the default should also specify number formatting patterns that are appropriate for use within the context of the given numbering system. For more information on numbering systems and their definitions, see Section 1: Numbering Systems.
2.4.1 Compact Number Formats
A pattern type attribute is used for compact number formats, such as the following:
Formats can be supplied for numbers (as above) or for currencies or other units. They can also be used with ranges of numbers, resulting in formatting strings like “$10K” or “$3–7M”.
To format a number N, the greatest type less than or equal to N is used, with the appropriate plural category. N is divided by the type, after removing the number of zeros in the pattern, less 1. APIs supporting this format should provide control over the number of significant or fraction digits.
The default pattern for any type that is not supplied is the special value “0”, as in the following. The value “0” must be used when a child locale overrides a parent locale to drop the compact pattern for that type and use the default pattern.
With the data above, N=12345 matches
. N is divided by 1000 (obtained from10000 after removing «00» and restoring one «0». The result is formatted according to the normal decimal pattern. With no fractional digits, that yields «12 K».
The short format is designed for UI environments where space is at a premium, and should ideally result in a formatted string no more than about 6 em wide (with no fractional digits).
2.4.2 Currency Formats
In addition to a standard currency format, in which negative currency amounts might typically be displayed as something like “-$3.27”, locales may provide an «accounting» form, in which for «en_US» the same example would appear as “($3.27)”.
2.5 Miscellaneous Patterns
The miscPatterns supply additional patterns for special purposes. The currently defined values are:
approximately
indicates an approximate number, such as: “
99”. This pattern is not currently in use; see ICU-20163.
atMost
indicates a number or lower, such as: “ ≤ 99” to indicate that there are 99 items or fewer.
atLeast
indicates a number or higher, such as: “99+” to indicate that there are 99 items or more.
range
indicates a range of numbers, such as: “99–103” to indicate that there are from 99 to 103 items.
2.6 Minimal Pairs
3 Number Format Patterns
3.1 Number Patterns
Number patterns affect how numbers are interpreted in a localized context. Here are some examples, based on the French locale. The «.» shows where the decimal point should go. The «,» shows where the thousands separator should go. A «0» indicates zero-padding: if the number is too short, a zero (in the locale’s numeric set) will go there. A «#» indicates no padding: if the number is too short, nothing goes there. A «¤» shows where the currency sign will go. The following illustrates the effects of different patterns for the French locale, with the number «1234.567». Notice how the pattern characters ‘,’ and ‘.’ are replaced by the characters appropriate for the locale.
| Pattern | Currency | Text |
|---|---|---|
| #,##0.## | n/a | 1 234,57 |
| #,##0.### | n/a | 1 234,567 |
| ###0.##### | n/a | 1234,567 |
| ###0.0000# | n/a | 1234,5670 |
| 00000.0000 | n/a | 01234,5670 |
| #,##0.00 ¤ | EUR | 1 234,57 € |
| JPY | 1 235 ¥JP |
The number of # placeholder characters before the decimal do not matter, since no limit is placed on the maximum number of digits. There should, however, be at least one zero someplace in the pattern. In currency formats, the number of digits after the decimal also do not matter, since the information in the supplemental data (see Supplemental Currency Data) is used to override the number of decimal places — and the rounding — according to the currency that is being formatted. That can be seen in the above chart, with the difference between Yen and Euro formatting.
To ensure correct layout, especially in currency patterns in which a a variety of symbols may be used, number patterns may contain (invisible) bidirectional text format characters such as LRM, RLM, and ALM.
When parsing using a pattern, a lenient parse should be used; see Lenient Parsing. As noted there, lenient parsing should ignore bidi format characters.
3.2 Special Pattern Characters
Many characters in a pattern are taken literally; they are matched during parsing and output unchanged during formatting. Special characters, on the other hand, stand for other characters, strings, or classes of characters. For example, the ‘#’ character is replaced by a localized digit for the chosen numberSystem. Often the replacement character is the same as the pattern character; in the U.S. locale, the ‘,’ grouping character is replaced by ‘,’. However, the replacement is still happening, and if the symbols are modified, the grouping character changes. Some special characters affect the behavior of the formatter by their presence; for example, if the percent character is seen, then the value is multiplied by 100 before being displayed.
To insert a special character in a pattern as a literal, that is, without any special meaning, the character must be quoted. There are some exceptions to this which are noted below. The Localized Replacement column shows the replacement from Section 2.3 Number Symbols or the numberSystem’s digits: italic indicates a special function.
Invalid sequences of special characters (such as “¤¤¤¤¤¤” in current CLDR) should be handled for formatting and parsing as described in Handling Invalid Patterns.
A pattern contains a positive subpattern and may contain a negative subpattern, for example, «#,##0.00;(#,##0.00)». Each subpattern has a prefix, a numeric part, and a suffix. If there is no explicit negative subpattern, the implicit negative subpattern is the ASCII minus sign (-) prefixed to the positive subpattern. That is, «0.00» alone is equivalent to «0.00;-0.00». (The data in CLDR is normalized to remove an explicit negative subpattern where it would be identical to the implicit form.)
If there is an explicit negative subpattern, it serves only to specify the negative prefix and suffix; the number of digits, minimal digits, and other characteristics are ignored in the negative subpattern. That means that «#,##0.0#;(#)» has precisely the same result as «#,##0.0#;(#,##0.0#)». However in the CLDR data, the format is normalized so that the other characteristics are preserved, just for readability.
A currency decimal pattern normally contains a currency symbol placeholder (¤, ¤¤, ¤¤¤, or ¤¤¤¤¤). The currency symbol placeholder may occur before the first digit, after the last digit symbol, or where the decimal symbol would otherwise be placed (for formats such as «12€50», as in «12€50 pour une omelette»).
Below is a sample of patterns, special characters, and results:
| explicit pattern: | 0.00;-0.00 | 0.00;0.00- | 0.00+;0.00- | |||
|---|---|---|---|---|---|---|
| decimalSign: | , | , | , | |||
| minusSign: | ∸ | ∸ | ∸ | |||
| plusSign: | ∔ | ∔ | ∔ | |||
| number: | 3.1415 | -3.1415 | 3.1415 | -3.1415 | 3.1415 | -3.1415 |
| formatted: | 3,14 | ∸3,14 | 3,14 | 3,14∸ | 3,14∔ | 3,14∸ |
In the above table, ∸ = U+2238 DOT MINUS and ∔ = U+2214 DOT PLUS are used for illustration.
The prefixes, suffixes, and various symbols used for infinity, digits, thousands separators, decimal separators, and so on may be set to arbitrary values, and they will appear properly during formatting. However, care must be taken that the symbols and strings do not conflict, or parsing will be unreliable. For example, either the positive and negative prefixes or the suffixes must be distinct for any parser using this data to be able to distinguish positive from negative values. Another example is that the decimal separator and thousands separator should be distinct characters, or parsing will be impossible.
The grouping separator is a character that separates clusters of integer digits to make large numbers more legible. It is commonly used for thousands, but in some locales it separates ten-thousands. The grouping size is the number of digits between the grouping separators, such as 3 for «100,000,000» or 4 for «1 0000 0000». There are actually two different grouping sizes: One used for the least significant integer digits, the primary grouping size, and one used for all others, the secondary grouping size. In most locales these are the same, but sometimes they are different. For example, if the primary grouping interval is 3, and the secondary is 2, then this corresponds to the pattern «#,##,##0», and the number 123456789 is formatted as «12,34,56,789». If a pattern contains multiple grouping separators, the interval between the last one and the end of the integer defines the primary grouping size, and the interval between the last two defines the secondary grouping size. All others are ignored, so «#,##,###,####» == «###,###,####» == «##,#,###,####».
The grouping separator may also occur in the fractional part, such as in “#,##0.###,#”. This is most commonly done where the grouping separator character is a thin, non-breaking space (U+202F), such as “1.618 033 988 75”. See physics.nist.gov/cuu/Units/checklist.html.
For consistency in the CLDR data, the following conventions are observed:
All number patterns should be minimal: there should be no leading # marks except to specify the position of the grouping separators (for example, avoid ##,##0.###).
All formats should have one 0 before the decimal point (for example, avoid #,###.##)
Decimal formats should have three hash marks in the fractional position (for example, #,##0.###).
Currency formats should have two zeros in the fractional position (for example, ¤ #,##0.00).
The only time two thousands separators needs to be used is when the number of digits varies, such as for Hindi: #,##,##0.
The minimumGroupingDigits can be used to suppress groupings below a certain value. This is used for languages such as Polish, where one would only write the grouping separator for values above 9999. The minimumGroupingDigits contains the default for the locale.
The attribute value is used by adding it to the grouping separator value. If the input number has fewer integer digits, the grouping separator is suppressed.
Examples of minimumGroupingDigits
| minimumGroupingDigits | Pattern Grouping | Input Number | Formatted |
|---|---|---|---|
| 1 | 3 | 1000 | 1,000 |
| 1 | 3 | 10000 | 10,000 |
| 2 | 3 | 1000 | 1000 |
| 2 | 3 | 10000 | 10,000 |
| 1 | 4 | 10000 | 1,0000 |
| 2 | 4 | 10000 | 10000 |
3.2.1 Explicit Plus Signs
An explicit «plus» format can be formed, so as to show a visible + sign when formatting a non-negative number. The displayed plus sign can be an ASCII plus or another character, such as ＋ U+FF0B FULLWIDTH PLUS SIGN or ➕ U+2795 HEAVY PLUS SIGN; it is taken from whatever is set for plusSign in Section 2.3 Number Symbols.
3.3 Formatting
Formatting is guided by several parameters, all of which can be specified either using a pattern or using an external API designed for number formatting. The following description applies to formats that do not use scientific notation or significant digits.
Special Values
3.4 Scientific Notation
Numbers in scientific notation are expressed as the product of a mantissa and a power of ten, for example, 1234 can be expressed as 1.234 x 103. The mantissa is typically in the half-open interval [1.0, 10.0) or sometimes [0.0, 1.0), but it need not be. In a pattern, the exponent character immediately followed by one or more digit characters indicates scientific notation. Example: «0.###E0» formats the number 1234 as «1.234E3».
The number of digit characters after the exponent character gives the minimum exponent digit count. There is no maximum. Negative exponents are formatted using the localized minus sign, not the prefix and suffix from the pattern. This allows patterns such as «0.###E0 m/s». To prefix positive exponents with a localized plus sign, specify ‘+’ between the exponent and the digits: «0.###E+0» will produce formats «1E+1», «1E+0», «1E-1», and so on. (In localized patterns, use the localized plus sign rather than ‘+’.)
The minimum number of integer digits is achieved by adjusting the exponent. Example: 0.00123 formatted with «00.###E0» yields «12.3E-4». This only happens if there is no maximum number of integer digits. If there is a maximum, then the minimum number of integer digits is fixed at one.
The maximum number of integer digits, if present, specifies the exponent grouping. The most common use of this is to generate engineering notation, in which the exponent is a multiple of three, for example, «##0.###E0». The number 12345 is formatted using «##0.####E0» as «12.345E3».
When using scientific notation, the formatter controls the digit counts using logic for significant digits. The maximum number of significant digits comes from the mantissa portion of the pattern: the string of #, 0, and period («.») characters immediately preceding the E. To get the maximum number of significant digits, use the following algorithm:
Exponential patterns may not contain grouping separators.
3.5 Significant Digits
There are two ways of controlling how many digits are shows: (a) significant digits counts, or (b) integer and fraction digit counts. Integer and fraction digit counts are described above. When a formatter is using significant digits counts, it uses however many integer and fraction digits are required to display the specified number of significant digits. It may ignore min/max integer/fraction digits, or it may use them to the extent possible.
3.6 Padding
3.7 Rounding
Patterns support rounding to a specific increment. For example, 1230 rounded to the nearest 50 is 1250. Mathematically, rounding to specific increments is performed by dividing by the increment, rounding to an integer, then multiplying by the increment. To take a more bizarre example, 1.234 rounded to the nearest 0.65 is 1.3, as follows:
| Original: | 1.234 |
|---|---|
| Divide by increment (0.65): | 1.89846… |
| Round: | 2 |
| Multiply by increment (0.65): | 1.3 |
To specify a rounding increment in a pattern, include the increment in the pattern itself. «#,#50» specifies a rounding increment of 50. «#,##0.05» specifies a rounding increment of 0.05.
3.8 Quoting Rules
4 Currencies
Note: The term «pattern» appears twice in the above. The first is for consistency with all other cases of pattern + displayName; the second is for backwards compatibility.
The count attribute distinguishes the different plural forms, such as in the following:
Note on displayNames:
To format a particular currency value «ZWD» for a particular numeric value n using the (long) display name:
While for English this may seem overly complex, for some other languages different plural forms are used for different unit types; the plural forms for certain unit types may not use all of the plural-form tags defined for the language.
For example, if the the currency is ZWD and the number is 1234, then the latter maps to count=»other» for English. The unit pattern for that is » <0><1>«, and the display name is «Zimbabwe dollars». The final formatted number is then «1,234 Zimbabwe dollars».
When the currency symbol is substituted into a pattern, there may be some further modifications, according to the following.
Conversely, look at the pattern «¤#,##0.00» with the symbol «US$». In this case, there is no insertion; the result is simply «US$#,##0.00». The afterCurrency element governs this case, since we are looking after the «¤» symbol. The surroundingMatch is positive, since the character just after the «¤» will be a digit. However, the currencyMatch is not positive, since the «$» in «US$» is at the end of the currency symbol being substituted. So the insertion is not made.
For more information on the matching used in the currencyMatch and surroundingMatch elements, see the main document Appendix E: Unicode Sets.
Currencies can also contain optional grouping, decimal data, and pattern elements. This data is inherited from the in the same locale data (if not present in the chain up to root), so only the differing data will be present. See the main document Section 4.1 Multiple Inheritance.
Notice that the currency code is completely independent of the end-user’s language or locale. For example, BGN is the code for Bulgarian Lev. A currency amount of would be localized for a Bulgarian user into «1 234,56 лв.» (using Cyrillic letters). For an English user it would be localized into the string «BGN 1,234.56» The end-user’s language is needed for doing this last localization step; but that language is completely orthogonal to the currency code needed in the data. After all, the same English user could be working with dozens of currencies. Notice also that the currency code is also independent of whether currency values are inter-converted, which requires more interesting financial processing: the rate of conversion may depend on a variety of factors.
Thus logically speaking, once a currency amount is entered into a system, it should be logically accompanied by a currency code in all processing. This currency code is independent of whatever the user’s original locale was. Only in badly-designed software is the currency code (or equivalent) not present, so that the software has to «guess» at the currency code based on the user’s locale.
Note: The number of decimal places and the rounding for each currency is not locale-specific data, and is not contained in the Locale Data Markup Language format. Those values override whatever is given in the currency numberFormat. For more information, see Supplemental Currency Data.
For background information on currency names, see [CurrencyInfo].
4.1 Supplemental Currency Data
Each currencyData element contains one fractions element followed by one or more region elements. Here is an example for illustration.
The fractions element contains any number of info elements, with the following attributes:
For example, the following line
should cause the value 2.006 to be displayed as “2.01”, not “2.00”.
Each region element contains one attribute:
And can have any number of currency elements, with the ordered subelements.
That is, each currency element will list an interval in which it was valid. The ordering of the elements in the list tells us which was the primary currency during any period in time. Here is an example of such an overlap:
The from element is limited by the fact that ISO 4217 does not go very far back in time, so there may be no ISO code for the previous currency.
Currencies change relatively frequently. There are different types of changes:
The UN Information is used to determine dates due to country changes.
When a code is no longer in use, it is terminated (see #1, #2, #4, #5)
When codes split, each of the new codes inherits (see #2, #3) the previous data. However, some modifications can be made if it is clear that currencies were only in use in one of the parts.
When codes merge, the data is copied from the most populous part.
Example. When CS split into RS and ME:
5 Language Plural Rules
The plural categories are used to format messages with numeric placeholders, expressed as decimal numbers. The fundamental rule for determining plural categories is the existence of minimal pairs: whenever two different numbers may require different versions of the same message, then the numbers have different plural categories.
This happens even if nouns are invariant; even if all English nouns were invariant (like “sheep”), English would still require 2 plural categories because of subject-verb agreement, and pronoun agreement. For example:
English does not have a separate plural category for “zero”, because it does not require a different message for “0”. For example, the same message can be used below, with just the numeric placeholder changing.
However, across many languages it is commonly more natural to express «0» messages with a negative (“None of your friends are online.”) and «1» messages also with an alternate form “You have a friend online.”. Thus pluralized message APIs should also offer the ability to specify at least the 0 and 1 cases explicitly; developers can use that ability whenever these values might occur in a placeholder.
The CLDR plural rules are not expected to cover all cases. For example, strictly speaking, there could be more plural and ordinal forms for English. Formally, we have a different plural form where a change in digits forces a change in the rest of the sentence. There is an edge case in English because of the behavior of «a/an».
For example, in changing from 3 to 8:
So numbers of the following forms could have a special plural category and special ordinal category: 8(X), 11(X), 18(X), 8x(X), where x is 0..9 and the optional X is 00, 000, 00000, and so on.
On the other hand, the above constructions are relatively rare in messages constructed using numeric placeholders, so the disruption for implementations currently using CLDR plural categories wouldn’t be worth the small gain.
This section defines the types of plural forms that exist in a language—namely, the cardinal and ordinal plural forms. Cardinal plural forms express units such as time, currency or distance, used in conjunction with a number expressed in decimal digits (i.e. «2», not «two», and not an indefinite number such as «some» or «many»). Ordinal plural forms denote the order of items in a set and are always integers. For example, English has two forms for cardinals:
and four forms for ordinals:
Other languages may have additional forms or only one form for each type of plural. CLDR provides the following tags for designating the various plural forms of a language; for a given language, only the tags necessary for that language are defined, along with the specific numeric ranges covered by each tag (for example, the plural form «few» may be used for the numeric range 2–4 in one language and 3–9 in another):
In addition, an «other» tag is always implicitly defined to cover the forms not explicitly designated by the tags defined for a language. This «other» tag is also used for languages that only have a single form (in which case no plural-form tags are explicitly defined for the language). For a more complex example, consider the cardinal rules for Russian and certain other languages:
These rules specify that Russian has a «one» form (for 1, 21, 31, 41, 51, …), a «few» form (for 2–4, 22–24, 32–34, …), and implicitly an «other» form (for everything else: 0, 5–20, 25–30, 35–40, …, decimals). Russian does not need additional separate forms for zero, two, or many, so these are not defined.
A source number represents the visual appearance of the digits of the result. In text, it can be represented by the EBNF for sampleValue. Note that the same double number can be represented by multiple source numbers. For example, «1.0» and «1.00» are different source numbers, but there is only one double number that they correspond to: 1.0d == 1.00d. As another example, 1e3d == 1000d, but the source numbers «1e3» and «1000» are different, and can have different plural categories. So the input to the plural rules carries more information than a computer double. The plural category for negative numbers is calculated according to the absolute value of the source number, and leading integer digits don’t have any effect on the plural category calculation. (This may change in the future, if we find languages that have different behavior.)
Plural categories may also differ according to the visible decimals. For example, here are some of the behaviors exhibited by different languages:
| Behavior | Description | Example |
|---|---|---|
| Base | The fractions are ignored; the category is the same as the category of the integer. | 1.13 has the same plural category as 1. |
| Separate | All fractions by value are in one category (typically ‘other’ = ‘plural’). | 1.01 gets the same class as 9; 1.00 gets the same category as 1. |
| Visible | All visible fractions are in one category (typically ‘other’ = ‘plural). | 1.00, 1.01, 3.5 all get the same category. |
| Digits | The visible fraction determines the category. | 1.13 gets the same class as 13. |
There are also variants of the above: for example, short fractions may have the Digits behavior, but longer fractions may just look at the final digit of the fraction.
Explicit 0 and 1 rules
By contrast, for the explicit cases “0” and “1”:
Usage example: In English (which only defines language-specific rules for “one” and “other”) this can be used to have special behavior for 0:
5.1 Plural rules syntax
The xml value for each pluralRule is a condition with a boolean result. That value specifies whether that rule (i.e. that plural form) applies to a given source number N in sampleValue syntax, where N can be expressed as a decimal fraction or with compact decimal formatting. The compact decimal formatting is denoted by a special notation in the syntax, e.g., “1.2c6” for “1.2M”. Clients of CLDR may express all the rules for a locale using the following syntax:
In CLDR, the keyword is the attribute value of ‘count’. Those values in CLDR are currently limited to just what is in the DTD, but clients may support other values.
The conditions themselves have the following syntax.
5.1.1 Operands
The operands are numeric values corresponding to features of the source number N, and have the following meanings given in the table below. Note that, contrary to source numbers, operands are treated numerically. Although some of them are used to describe insignificant 0s in the source number, any insignificant 0s in the operands themselves are ignored, e.g., f=03 is equivalent to f=3.
| Symbol | Value |
|---|---|
| n | the absolute value of N.* |
| i | the integer digits of N.* |
| v | the number of visible fraction digits in N, with trailing zeros.* |
| w | the number of visible fraction digits in N, without trailing zeros.* |
| f | the visible fraction digits in N, with trailing zeros, expressed as an integer.* |
| t | the visible fraction digits in N, without trailing zeros, expressed as an integer.* |
| c | compact decimal exponent value: exponent of the power of 10 used in compact decimal formatting. |
| e | a deprecated synonym for ‘c’. Note: it may be redefined in the future. |
* If there is a compact decimal exponent value (‘c’), then the n, i, f, t, v, and w values are computed after shifting the decimal point in the original by the ‘c’ value. So for 1.2c3, the n, i, f, t, v, and w values are the same as those of 1200: i=1200 and f=0. Similarly, 1.2005c3 has i=1200 and f=5 (corresponding to 1200.5).
| source | n | i | v | w | f | t | e |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1.0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1.00 | 1 | 1 | 2 | 0 | 0 | 0 | 0 |
| 1.3 | 1.3 | 1 | 1 | 1 | 3 | 3 | 0 |
| 1.30 | 1.3 | 1 | 2 | 1 | 30 | 3 | 0 |
| 1.03 | 1.03 | 1 | 2 | 2 | 3 | 3 | 0 |
| 1.230 | 1.23 | 1 | 3 | 2 | 230 | 23 | 0 |
| 1200000 | 1200000 | 1200000 | 0 | 0 | 0 | 0 | 0 |
| 1.2c6 | 1200000 | 1200000 | 0 | 0 | 0 | 0 | 6 |
| 123c6 | 123000000 | 123000000 | 0 | 0 | 0 | 0 | 6 |
| 123c5 | 12300000 | 12300000 | 0 | 0 | 0 | 0 | 5 |
| 1200.50 | 1200.5 | 1200 | 2 | 1 | 50 | 5 | 0 |
| 1.20050c3 | 1200.5 | 1200 | 2 | 1 | 50 | 5 | 3 |
5.1.2 Relations
The positive relations are of the format x = y and x = y mod z. The y value can be a comma-separated list, such as n = 3, 5, 7..15, and is treated as if each relation were expanded into an OR statement. The range value a..b is equivalent to listing all the _integers_ between a and b, inclusive. When != is used, it means the entire relation is negated.
The old keywords ‘mod’, ‘in’, ‘is’, and ‘within’ are present only for backwards compatibility. The preferred form is to use ‘%’ for modulo, and ‘=’ or ‘!=’ for the relations, with the operand ‘i’ instead of within. (The difference between in and within is that in only includes integers in the specified range, while within includes all values.)
The modulus (% or mod) is a remainder operation as defined in Java; for example, where n = 4.3 the result of n mod 3 is 1.3.
The values of relations are defined according to the operand as follows. Importantly, the results may depend on the visible decimals in the source, including trailing zeros, and the compact decimal exponent.
5.1.3 Samples
Samples are provided if sample indicator (@integer or @decimal) is present on any rule. (CLDR always provides samples.)
Where samples are provided, the absence of one of the sample indicators indicates that no numeric values can satisify that rule. For example, the rule «i = 1 and v = 0» can only have integer samples, so @decimal must not occur. The @integer samples have no visible fraction digits, while @decimal samples have visible fraction digits; both can have compact decimal exponent values (if the ‘e’ operand occurs).
The sampleRanges have a special notation: start
end. The start and end values must have the same number of decimal digits, and the same compact decimal exponent values (or neither have compact decimal exponent values). The range encompasses all and only values those value v where start ≤ v ≤ end, and where v has the same number of decimal places as start and end, and the same compact decimal exponent values.
Samples must indicate whether they are infinite or not. The ‘…’ marker must be present if and only infinitely many values (integer or decimal) can satisfy the rule. If a set is not infinite, it must list all the possible values.
| Rules | Comments |
|---|---|
| @integer 1, 3 5 | 1, 3, 4, 5. |
| @integer 3 105, … | Infinite set: 3, 4, 5, 103, 104, 105, … |
| @decimal 1.3 1.05, … | Infinite set: 1.3, 1.4, 1.5, 1.03, 1.04, 1.05, … |
In determining whether a set of samples is infinite, leading zero integer digits and trailing zero decimals are not significant. Thus «i = 1000 and f = 0» is satisfied by 01000, 1000, 1000.0, 1000.00, 1000.000, 01c3 etc. but is still considered finite.
5.1.4 Using Cardinals
5.2 Plural Ranges
Often ranges of numbers are presented to users, such as in “Length: 3.2–4.5 centimeters”. This means any length from 3.2 cm to 4.5 cm, inclusive. However, different languages have different conventions for the pluralization given to a range: should it be “0–1 centimeter” or “0–1 centimeters”? This becomes much more complicated for languages that have many different plural forms, such as Russian or Arabic.
The data has been gathered presuming that in any usage, the start value is strictly less than the end value, and that no values are negative. Results for any cases that do not meet these criteria are undefined.
For the formatting of number ranges, see Number Range Formatting.
6 Rule-Based Number Formatting
The rule-based number format (RBNF) encapsulates a set of rules for mapping binary numbers to and from a readable representation. They are typically used for spelling out numbers, but can also be used for other number systems like roman numerals, Chinese numerals, or for ordinal numbers (1st, 2nd, 3rd,…).
Where, however, the CLDR plurals or ordinals can be used, their usage is recommended in preference to the RBNF data. First, the RBNF data is not completely fleshed out over all languages that otherwise have modern coverage. Secondly, the alternate forms are neither complete, nor useful without additional information. For example, for German there is spellout-cardinal-masculine, and spellout-cardinal-feminine. But a complete solution would have all genders (masculine/feminine/neuter), all cases (nominative, accusative, dative, genitive), plus context (with strong or weak determiner or none). Moreover, even for the alternate forms that do exist, CLDR does not supply any data for when to use one vs another (eg, when to use spellout-cardinal-masculine vs spellout-cardinal-feminine). So these data are inappropriate for general purpose software.
There are 4 common spellout rules. Some languages may provide more than these 4 types:
In addition to the spellout rules, there are also a numbering system rules. Even though they may be derived from a specific culture, they are typically not translated and the rules are in root. An example of these rules are the Roman numerals where the value 8 comes out as VIII.
With regards to the number range supported for all these number types, the largest possible number range tries to be supported, but some languages may not have words for large numbers. For example, the old Roman numbering system can’t support the value 5000 and beyond. For those unsupported cases, the default number format from CLDR is used.
Any rules marked as private should never be referenced externally. Frequently they only support a subrange of numbers that are used in the public rules.
The syntax used in the CLDR representation of rules is intended to be simply a transcription of ICU based RBNF rules into an XML compatible syntax. The rules are fairly sophisticated; for details see Rule-Based Number Formatter [RBNF].
Used to group rules into functional sets for use with ICU. Currently, the valid types of rule set groupings are «SpelloutRules», «OrdinalRules», and «NumberingSystemRules».
This element denotes a specific rule set to the number formatter. The ruleset is assumed to be a public ruleset unless the attribute type=»private» is specified.
Contains the actual formatting rule for a particular number or sequence of numbers. The value attribute is used to indicate the starting number to which the rule applies. The actual text of the rule is identical to the ICU syntax, with the exception that Unicode left and right arrow characters are used to replace in the rule text, since are reserved characters in XML. The radix attribute is used to indicate an alternate radix to be used in calculating the prefix and postfix values for number formatting. Alternate radix values are typically used for formatting year numbers in formal documents, such as «nineteen hundred seventy-six» instead of «one thousand nine hundred seventy-six».
7 Parsing Numbers
The following elements are relevant to determining the value of a parsed number:
Other characters should either be ignored, or indicate the end of input, depending on the application. The key point is to disambiguate the sets of characters that might serve in more than one position, based on context. For example, a period might be either the decimal separator, or part of a currency symbol (for example, «NA f.»). Similarly, an «E» could be an exponent indicator, or a currency symbol (the Swaziland Lilangeni uses «E» in the «en» locale). An apostrophe might be the decimal separator, or might be the grouping separator.
Here is a set of heuristic rules that may be helpful:
Any character with the decimal digit property is unambiguous and should be accepted.
Note: In some environments, applications may independently wish to restrict the decimal digit set to prevent security problems. See [UTR36].
The exponent character can only be interpreted as such if it occurs after at least one digit, and if it is followed by at least one digit, with only an optional sign in between. A regular expression may be helpful here.
For the sign, decimal separator, percent, and per mille, use a set of all possible characters that can serve those functions. For example, the decimal separator set could include all of [.,’]. (The actual set of characters can be derived from the number symbols in the By-Type charts [ByType], which list all of the values in CLDR.) To disambiguate, the decimal separator for the locale must be removed from the «ignore» set, and the grouping separator for the locale must be removed from the decimal separator set. The same principle applies to all sets and symbols: any symbol must appear in at most one set.
Since there are a wide variety of currency symbols and codes, this should be tried before the less ambiguous elements. It may be helpful to develop a set of characters that can appear in a symbol or code, based on the currency symbols in the locale.
Otherwise, a character should be ignored unless it is in the «stop» set. This includes even characters that are meaningful for formatting, for example, the grouping separator.
If more than one sign, currency symbol, exponent, or percent/per mille occurs in the input, the first found should be used.
A currency symbol in the input should be interpreted as the longest match found in the set of possible currency symbols.
Especially in cases of ambiguity, the user’s input should be echoed back, properly formatted according to the locale, before it is actually used for anything.
8 Number Range Formatting
Often ranges of numbers are presented to users, such as in “Length: 3.2–4.5 centimeters”. This means any length from 3.2 cm to 4.5 cm, inclusive.
To format a number range, the following steps are taken:
* Semantic annotations are discussed in Collapsing Number Ranges.
For plural rule selection of number ranges, see Plural Ranges.
8.1 Approximate Number Formatting
Approximate number formatting refers to a specific format of numbers in which the value is understood to not be exact; for example, «
To format an approximate number, follow the normal number formatting procedure in Number Format Patterns](#Number_Format_Patterns), but substitute the approximatelySign from Number Symbols in for the minus sign placeholder.
If the number is negative, or if the formatting options request the sign to be displayed, prepend the approximatelySign to the plus or minus sign before substituting it into the pattern. For example, «
-5″ means «approximately negative five». This procedure may change in the future.
8.2 Collapsing Number Ranges
Collapsing a number range refers to the process of removing duplicated information in the lower and upper values. For example, if the lower string is «3.2 centimeters» and the upper string is «4.5 centimeters», it is desirable to remove the extra «centimeters» token.
This operation requires semantic annotations on the formatted value. The exact form of the semantic annotations is implementation-dependent. However, implementations may consider the following broad categories of tokens:
Two tokens are semantically equivalent if they have the same semantic annotations, even if they are not the exact same string. For example:
The above description describes the expected output. Internally, the implementation may determine the equivalent units of measurement by passing the codes back from the number formatters, allowing for a precise determination of «semantically equivalent».
Two semantically equivalent tokens can be collapsed if they appear at the start of both values or the end of both values. However, the implementation may choose different levels of aggressiveness with regard to collapsing tokens. The currently recommended heuristic is:
These heuristics may be refined in the future.
To collapse tokens: Remove the token from both values, and then re-compute the token based on the number range. If the token depends on the plural form, follow Plural Ranges to calculate the correct form. If the tokens originated at the beginning of the string, prepend the new token to the beginning of the lower string; otherwise, append the new token to the end of the upper string.
8.3 Range Pattern Processing
To obtain a number range pattern, the following steps are taken:
To determine whether to add spacing, the currently recommended heuristic is:
These heuristics may be refined in the future.
To add spacing, insert a non-breaking space (U+00A0) at the positions in item 2 above.
Copyright © 2001–2022 Unicode, Inc. All Rights Reserved. The Unicode Consortium makes no expressed or implied warranty of any kind, and assumes no liability for errors or omissions. No liability is assumed for incidental and consequential damages in connection with or arising out of the use of the information or programs contained or accompanying this technical report. The Unicode Terms of Use apply.
Unicode and the Unicode logo are trademarks of Unicode, Inc., and are registered in some jurisdictions.
Источники информации:
- http://www.officetooltips.com/office_2016/tips/how_to_change_decimal_symbol_and_digit_grouping_symbol_in_windows_10.html
- http://www.euston96.com/en/decimal-system/
- http://www.csee.umbc.edu/courses/undergraduate/313/fall04/burt_katz/lectures/Lect01/numberSystems.html
- http://unicode.org/reports/tr35/tr35-numbers.html