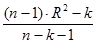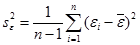что означает нормированный r квадрат в регрессионной статистике
Пакет анализа Excel (Регрессия)
Построение линейной регрессии, оценивание ее параметров и их значимости можно выполнить значительнее быстрей при использовании пакета анализа Excel (Регрессия). Рассмотрим интерпретацию полученных результатов в общем случае (k объясняющих переменных) по данным примера 3.5.
| Вывод итогов | |
| Регрессионная статистика | |
| Множественный R | 0,940 |
| R-квадрат | 0,884 |
| Нормированный R – квадрат | 0,868 |
| Стандартная ошибка | 22,87 |
| Наблюдения |
В таблице регрессионной статистики приводятся значения:
Множественный R – коэффициент множественной корреляции 
R—квадрат – коэффициент детерминации R 2 ;
Нормированный R—квадрат – скорректированный R 2 с поправкой на число степеней свободы;
Стандартная ошибка– стандартная ошибка регрессии S;
Наблюдения –число наблюдений n.
| Дисперсионный анализ | ||||
| df | SS | MS | F | Значимость F |
| Регрессия | 28102,2 | 28102,2 | 53,69 | 0,00016 |
| Остаток | 3663,7 | 523,3 | ||
| Итого |
В таблице Дисперсионный анализприведены:
для строки Регрессия df = k;
для строкиОстатокdf = n – k – 1;
для строкиИтогоdf = n – 1.
2. Столбец SS –сумма квадратов отклонений, равная
для строки Регрессия 

для строкиОстаток 
для строкиИтого 
3. Столбец MSдисперсии, определяемые по формуле MS = SS/df:
для строки Регрессия – факторная дисперсия;
для строкиОстаток– остаточная дисперсия.
4. Столбец F – расчетное значение F-критерия, вычисляемое по формуле
5. Столбец Значимость F –значение уровня значимости, соответствующее вычисленной F-статистике.
Значимость F = FРАСП(F-статистика, df(регрессия), df(остаток)).
Если значимость F 2 статистически значим.
| Коэффи-циенты | Стандартная ошибка | t-cта-тистика | P-значение | Нижние 95% | Верхние 95% | |
| Y | 65,92 | 11,74 | 5,61 | 0,00080 | 38,16 | 93,68 |
| X | 0,107 | 0,014 | 7,32 | 0,00016 | 0,0728 | 0,142 |
В этой таблице указаны:
1. Коэффициенты– значения коэффициентов a, b.
2. Стандартная ошибка–стандартные ошибки коэффициентов регрессии Sa, Sb.
3. t-статистика – расчетные значения t-критерия, вычисляемые по формуле:
t-статистика = Коэффициенты / Стандартная ошибка.
4.Р-значение (значимость t)– это значение уровня значимости, соответствующее вычисленной t-статистике.
Р-значение = СТЬЮДРАСП(t-статистика, df(остаток)).
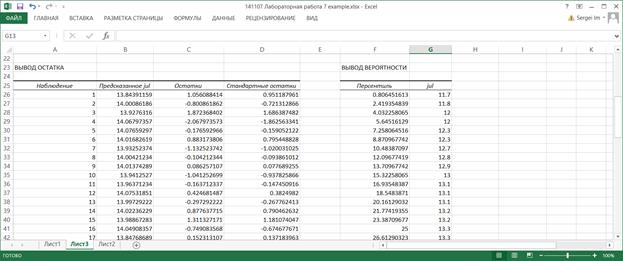
| ВЫВОД ОСТАТКА | ||
| Наблюдение | Предсказанное y | Остатки e |
| 72,70 | -29,70 | |
| 82,91 | -20,91 | |
| 94,53 | -4,53 | |
| 105,72 | 5,27 | |
| 117,56 | 12,44 | |
| 129,70 | 19,29 | |
| 144,22 | 20,77 | |
| 166,49 | 24,50 | |
| 268,13 | -27,13 |
В таблице ВЫВОД ОСТАТКАуказаны:
в столбце Наблюдение– номер наблюдения;
в столбце Предсказанное y– расчетные значения зависимой переменной;
в столбце Остатки e– разница между наблюдаемыми и расчетными значениями зависимой переменной.
Пример 3.6.Имеются данные (усл. ед.) о расходах на питание y и душевого дохода x для девяти групп семей:
Используя результаты работы пакета анализа Excel (Регрессия), проанализируем зависимость расходов на питание от величины душевого дохода.
Результаты регрессионного анализа принято записывать в виде:
где в скобках указаны стандартные ошибки коэффициентов регрессии.
Коэффициенты регрессии а = 65,92 и b = 0,107. Направление связи между y и xопределяет знак коэффициентарегрессии b = 0,107, т.е. связь является прямой и положительной. Коэффициент b = 0,107 показывает, что при увеличении душевого дохода на 1 усл. ед. расходы на питание увеличиваются на 0,107 усл. ед.
Оценим значимость коэффициентов полученной модели. Значимость коэффициентов (a, b) проверяется по t-тесту:
Р-значение (a) = 0,00080
Величина R 2 = 0,884 означает, что фактором душевого дохода можно объяснить 88,4 % вариации (разброса) расходов на питание.
Значимость R 2 проверяется по F-тесту: значимость F = 0,00016 2 значим при 1 %-ном уровне, а тем более при 5 %-ном уровне значимости.
В случае парной линейной регрессии коэффициент корреляции можно определить как 
R Квадрат Интерпретация | R квадрат линейная регрессия
Дата публикации Apr 30, 2019
Машинное обучение включает в себя много статистики. В следующей статье мы рассмотрим концепцию R-Squared, которая полезна при выборе функций.
Последнее звучит довольно запутанно, поэтому давайте рассмотрим пример. Предположим, мы решили построить график зависимости зарплаты от многолетнего опыта. На следующем графике каждая точка данных представляет человека.
Мы можем рассчитать среднее или среднее значение, взяв сумму всех лиц в выборке и разделив ее на общее количество людей в выборке.
Дисперсия всего набора данных равна сумме расстояния между каждой точкой данных и средним квадратом. Разница возводится в квадрат так, что баллы ниже среднего не отменяются баллами выше среднего.
Теперь скажем, мы взяли тех же людей, но на этот раз мы решили построить график зависимости их зарплаты от роста.
Обратите внимание, что средняя зарплата остается неизменной независимо от того, что мы считаем независимой переменной. Другими словами, мы можем использовать другие аспекты жизни людей какИксно зарплата останется прежней.
Предположим, что мы использовали линейную регрессию, чтобы найтилучший примерлиния.
Значениеr²затем может быть выражено как:
гдепеременная (средний)является дисперсия по отношению к среднему ивар (линия)это дисперсия по отношению к линии.
Как мы упоминали ранее, дисперсию можно рассчитать, взяв сумму разностей между отдельными зарплатами и средним квадратом.
Используя ту же логику, мы можем определить изменение вокруг оранжевой линии.
Предполагая, что мы получили следующие значения для дисперсии линии и среднего значения.
Мы можем рассчитатьr²используя формулу, описанную ранее.
Значение R2 означает, что отклонение по линии на 96% меньше, чем среднее значение. Другими словами, соотношение между заработной платой и многолетним опытом составляет 96%. Иными словами, многолетний опыт является хорошим предиктором заработной платы, потому что, когда годы растут, растет и зарплата, и наоборот.
Давайте посмотрим, как мы можем использовать R² для оценки модели линейной регрессии. Для начала импортируйте следующие библиотеки.
Мы будем использовать следующий набор данных. Если вы хотите следовать, скопируйте его содержимое в CSV-файл.
Мы загружаем данные в нашу программу, используя pandas, и наносим их на график, используя matplotlib.
Далее мы обучаем модель линейной регрессии нашим данным о заработной плате.
Мы можем просмотреть лучшую линию подгонки, произведенную нашей моделью, запустив следующие линии.
Затем мы вычисляем R², используя формулу, рассмотренную в предыдущем разделе.
Вместо того, чтобы реализовывать его с нуля каждый раз, мы можем использовать sklearn r2_score функция.
R-квадрат
Опубликовано 20.05.2020 · Обновлено 20.05.2021
Что такое R-квадрат?
R-квадрат (R 2 ) – это статистическая мера, которая представляет долю дисперсии для зависимой переменной, которая объясняется независимой переменной или переменными в регрессионной модели. В то время как корреляция объясняет силу взаимосвязи между независимой и зависимой переменной, R-квадрат объясняет, в какой степени дисперсия одной переменной объясняет дисперсию второй переменной. Таким образом, если R 2 модели равен 0,50, то примерно половина наблюдаемой вариации может быть объяснена входными данными модели.
При инвестировании R-квадрат обычно интерпретируется как процент движений фонда или ценных бумаг, которые можно объяснить движениями эталонного индекса. Например, R-квадрат для ценной бумаги с фиксированным доходом по сравнению с индексом облигаций определяет долю движения цены ценной бумаги, которая предсказуема на основе движения цены индекса. То же самое можно применить к акции по сравнению с индексом S&P 500 или любым другим соответствующим индексом.
Формула для R-квадрата
Ключевые моменты
Расчет R-квадрат
Чтобы рассчитать общую дисперсию, вы должны вычесть среднее фактическое значение из каждого фактического значения, возвести результаты в квадрат и просуммировать их. Оттуда разделите первую сумму ошибок (объясненную дисперсию) на вторую сумму (общую дисперсию), вычтите результат из единицы, и вы получите R-квадрат.
Что вам говорит R-Squared?
Значения R-квадрат находятся в диапазоне от 0 до 1 и обычно выражаются в процентах от 0% до 100%. R-квадрат 100% означает, что все движения ценной бумаги (или другой зависимой переменной) полностью объясняются движениями индекса (или интересующих вас независимых переменных).
Разница между R-квадрат и скорректированный R-квадрат
Разница между R-Squared и Beta
Ограничения R-Squared
R-квадрат даст вам оценку взаимосвязи между движениями зависимой переменной на основе движений независимой переменной. Он не говорит вам, хороша ли ваша выбранная модель или плоха, и не говорит вам, являются ли данные и прогнозы необъективными. Высокий или низкий R-квадрат не обязательно хорош или плох, поскольку он не передает надежность модели или правильность выбора регрессии. Вы можете получить низкий R-квадрат для хорошей модели или высокий R-квадрат для плохо подогнанной модели, и наоборот.
Часто задаваемые вопросы
Что такое хорошее значение R-квадрат
То, что считается «хорошим» значением R-Squared, будет зависеть от контекста. В некоторых областях, таких как социальные науки, даже относительно низкий R-Squared, такой как 0,5, можно считать относительно сильным. В других областях стандарты хорошего показания R-Squared могут быть намного выше, например 0,9 или выше. В сфере финансов R-Squared выше 0,7 обычно рассматривается как показывающий высокий уровень корреляции, тогда как показатель ниже 0,4 показывает низкую корреляцию. Однако это не жесткое правило, и оно будет зависеть от конкретного анализа.
Что означает значение R-Squared 0,9?
По сути, значение R-Squared, равное 0,9, означает, что 90% дисперсии изучаемой зависимой переменной объясняется дисперсией независимой переменной. Например, если у паевого инвестиционного фонда значение R-Squared составляет 0,9 относительно его эталонного показателя, это будет означать, что 90% дисперсии фонда объясняется дисперсией его эталонного индекса.
Лучше ли более высокий R-квадрат?
Вычисление линейной регрессии



7.1. Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессионный анализ позволяет установить функциональную зависимость между некоторой случайной величиной Y и некоторыми влияющими на Y величинами X. Такая зависимость получила название уравнения регрессии. Различают простую (y=m*x+b) и множественную (y=m1*x1+m2*x2+. + mk*xk+b) регрессию линейного и нелинейного типа.
Для оценки степени связи между величинами используется коэффициент множественной корреляции R Пирсона (корреляционное отношение), который может принимать значения от 0 до 1. R=0, если между величинами нет никакой связи, и R=1, если между величинами имеется функциональная связь. В большинстве случаев R принимает промежуточные значения от 0 до 1. Величина R 2 называется коэффициентом детерминации.
Задачей построения регрессионной зависимости является нахождение вектора коэффициентов M модели множественной линейной регрессии, при котором коэффициент R принимает максимальное значение.
Для оценки значимости R применяется F-критерий Фишера, вычисляемый по формуле:
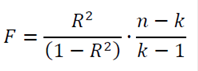
где n – количество экспериментов; k – число коэффициентов модели. Если F превышает некоторое критическое значение для данных n и k и принятой доверительной вероятности, то величина R считается существенной.
7.2. Инструмент Регрессия из Пакета анализа позволяет вычислить следующие данные:
· коэффициенты линейной функции регрессии– методом наименьших квадратов; вид функции регрессии определяется структурой исходных данных;
· коэффициент детерминации и связанные с ним величины (таблица Регрессионная статистика);
· дисперсионную таблицу и критериальную статистику для проверки значимости регрессии (таблица Дисперсионный анализ);
· среднеквадратическое отклонение и другие его статистические характеристики для каждого коэффициента регрессии, позволяющие проверить значимость этого коэффициента и построить для него доверительные интервалы;
· значения функции регрессии и остатки – разности между исходными значениями переменной Y и вычисленными значениями функции регрессии (таблица Вывод остатка);
· вероятности, соответствующие упорядоченным по возрастанию значениям переменной Y (таблица Вывод вероятности).
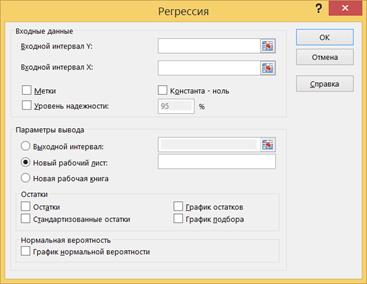
7.3. Вызовите инструмент создания выборки через Данные> Анализ данных> Регрессия.
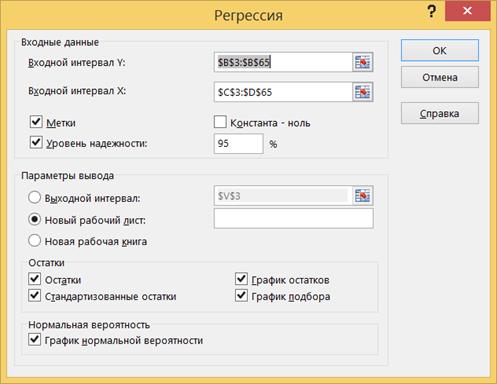
7.5. Установите параметры в соответствии с рисунком. Проверьте, что в качестве величины Y указана первая переменная (включая ячейку с названием), и в качестве величины X указаны две остальные переменные (включая ячейки с названиями). Нажмите OK.
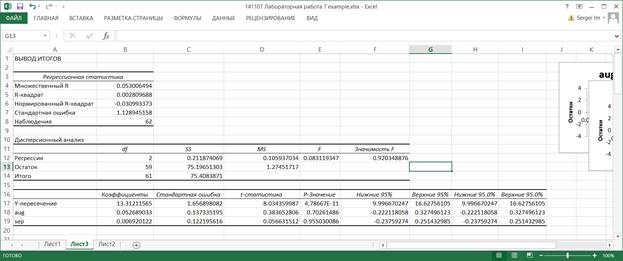
7.6. В таблице Регрессионная статистика приводятся следующие данные.
R-квадрат – коэффициент детерминации R 2 ; вычисляется как отношение регрессионной суммы квадратов (ячейка С12) к полной сумме квадратов (ячейка С14).
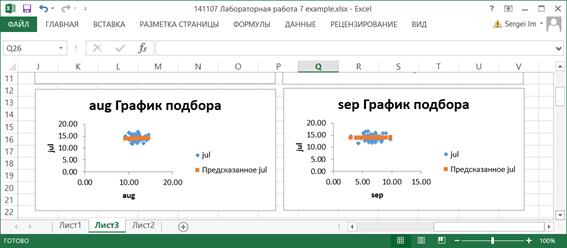
Нормированный R-квадрат вычисляется по формуле
где n – количество значений переменной Y, k – количество столбцов во входном интервале переменной X.
Стандартная ошибка – корень из остаточной дисперсии (ячейка D13).
Наблюдения – количество значений переменной Y.
7.7. В Дисперсионной таблице в столбце SS приводятся суммы квадратов, в столбце df – число степеней свободы. в столбце MS – дисперсии. В строке Регрессия в столбце f вычислено значение критериальной статистики для проверки значимости регрессии. Это значение вычисляется как отношение регрессионной дисперсии к остаточной (ячейки D12 и D13). В столбце Значимость F вычисляется вероятность полученного значения критериальной статистики. Если эта вероятность меньше, например, 0.05 (заданного уровня значимости), то гипотеза о незначимости регрессии (т.е. гипотеза о том, что все коэффициенты функции регрессии равны нулю) отвергается и считается, что регрессия значима. В данном примере регрессия незначима.
7.9. Рассмотрим таблицу Вывод остатка из выходных результатов. Эта таблица появляется в выходных результатах только тогда, когда установлена хотя бы одна опция в области Остатки диалогового окна Регрессия.
где 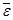
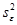
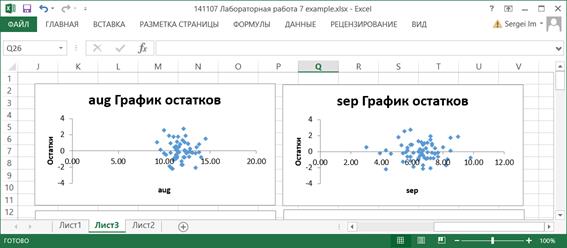
7.10. По значениям таблицы Вывод остатка строятся два типа графиков: графики остатков и графики подбора (если установлены соответствующие опции в области Остатки диалогового окна Регрессия). Они строятся для каждого компонента переменной X в отдельности.
На графиках остатков отображаются остатки, т.е. разности между исходными значениями Y и вычисленными по функции регрессии для каждого значения компонента переменной X.
На графиках подбора отображаются как исходные значения Y, так и вычисленные значения функции регрессии для каждого значения компонента переменной X.
7.11. Последней таблицей выходных результатов является таблица Вывод вероятности. Она появляется, если в диалоговом окне Регрессия установлена опция График нормальной вероятности.
Значения в столбце Персентиль вычисляются следующим образом. Вычисляется шаг h = (1/n)*100%, первое значение равно h/2, последнее равно 100-h/2. Начиная со второго значения каждое последующее значение равно предыдущему, к которому прибавлен шаг h.
В столбце Y приведены значения переменной Y, упорядоченные по возрастанию. По данным этой таблицы строится так называемый график нормального распределения. Он позволяет визуально оценить степень линейности зависимости между переменными X и Y.
8.1. Пакет анализа позволяет провести три вида дисперсионного анализа. Выбор конкретного инструмента определяется числом факторов и числом выборок в исследуемой совокупности данных.
Однофакторный дисперсионный анализ используется для проверки гипотезы о сходстве средних значений двух или более выборок, принадлежащих одной и той же генеральной совокупности.
Двухфакторный дисперсионный анализ с повторениями представляет собой более сложный вариант однофакторного анализа, включающий более чем одну выборку для каждой группы данных.
Двухфакторный дисперсионный анализ без повторения представляет собой двухфакторный анализ дисперсии, не включающий более одной выборки на группу. Он используется для проверки гипотезы о том, что средние значения двух или нескольких выборок одинаковы (выборки принадлежат одной и той же генеральной совокупности).
8.2. Однофакторный дисперсионный анализ
8.2.1. Подготовим данные для анализа. Создайте новый лист и скопируйте на него колонки A, B, C, D. Удалите первые две строки. Подготовленные данные можно использовать для проведения Однофакторного дисперсионного анализа.
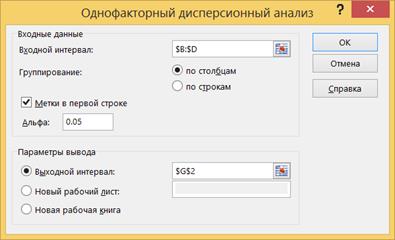
8.2.2. Вызовите инструмент создания выборки через Данные> Анализ данных> Однофакторный дисперсионный анализ.Заполните в соответствии с рисунком. Нажмите OK.
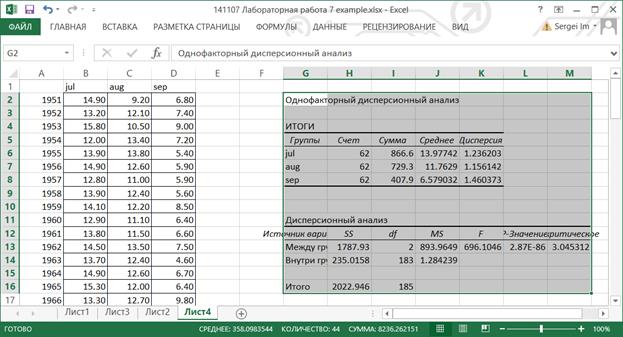
8.2.3. Рассмотрим таблицу Итоги: Счет – число повторений, Сумма – сумма значений показателя по строкам, Дисперсия – частная дисперсия показателя.
8.2.4. Таблица Дисперсионный анализ: первая колонка Источник вариации содержит наименование дисперсий, SS – сумма квадратов отклонений, df – степень свободы, MS – средний квадрат, F-критерий фактического F распределения. P-значение – вероятность того, что дисперсия, воспроизводимая уравнением, равна дисперсии остатков. Оно устанавливает вероятность того, что полученная количественная определенность взаимосвязи между факторами и результатом может считаться случайной. F-критическое – это значение F теоретического, которое впоследствии сравнивается с F фактическим.
8.2.5. Нулевая гипотеза о равенстве математических ожиданий всех выборок принимается, если выполняется неравенство F-критерий