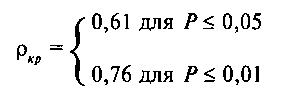что означает разность результатов ниже границы 0 05
Уровень статистической значимости



При обосновании статистического вывода следует решить вопрос, где же проходит линия между принятием и отвержением нулевой гипотезы? В силу наличия в эксперименте случайных влияний эта граница не может быть проведена абсолютно точно. Она базируется на понятии уровня значимости.Уровнемзначимостиназывается вероятность ошибочного отклонения нулевой гипотезы. Или, иными словами, уровеньзначимости—это вероятность ошибки первого рода при принятии решения. Для обозначения этой вероятности, как правило, употребляют либо греческую букву α, либо латинскую букву р. В дальнейшем мы будем употреблять букву р.
Исторически сложилось так, что в прикладных науках, использующих статистику, и в частности в психологии, считается, что низшим уровнем статистической значимости является уровень р = 0,05; достаточным — уровень р = 0,01 и высшим уровень р = 0,001. Поэтому в статистических таблицах, которые приводятся в приложении к учебникам по статистике, обычно даются табличные значения для уровней р = 0,05, р = 0,01 и р = 0,001. Иногда даются табличные значения для уровней р — 0,025 и р = 0,005.
Величины 0,05, 0,01 и 0,001 — это так называемые стандартные уровни статистической значимости. При статистическом анализе экспериментальных данных психолог в зависимости от задач и гипотез исследования должен выбрать необходимый уровень значимости. Как видим, здесь наибольшая величина, или нижняя граница уровня статистической значимости, равняется 0,05 — это означает, что допускается пять ошибок в выборке из ста элементов (случаев, испытуемых) или одна ошибка из двадцати элементов (случаев, испытуемых). Считается, что ни шесть, ни семь, ни большее количество раз из ста мы ошибиться не можем. Цена таких ошибок будет слишком велика.
Заметим, что в современных статистических пакетах на ЭВМ используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни, обозначаемые буквой р, могут иметь различное числовое выражение в интервале от 0 до 1, например, р = 0,7, р = 0,23 или р = 0,012. Понятно, что в первых двух случаях полученные уровни значимости слишком велики и говорить о том, что результат значим нельзя. В то же время в последнем случае результаты значимы на уровне 12 тысячных. Это достоверный уровень.
Правило принятия статистического вывода таково: на основании полученных экспериментальных данных психолог подсчитывает по выбранному им статистическому методу так называемую эмпирическую статистику, или эмпирическое значение. Эту величину удобно обозначить как Чэмп. Затем эмпирическая статистика Чэмп сравнивается с двумя критическими величинами, которые соответствуют уровням значимости в 5% и в 1% для выбранного статистического метода и которые обозначаются как Чкр. Величины Чкр находятся для данного статистического метода по соответствующим таблицам, приведенным в приложении к любому учебнику по статистике. Эти величины, как правило, всегда различны и их в дальнейшем для удобства можно назвать как Чкр1 и Чкр2. Найденные по таблицам величины критических значений Чкр1 и Чкр2 удобно представлять в следующей стандартной форме записи:
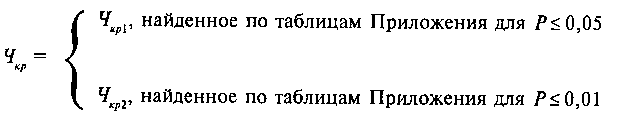 |
Подчеркнем, однако, что мы использовали обозначения Чэмп и Чкр как сокращение слова «число». Во всех статистических методах приняты свои символические обозначения всех этих величин: как подсчитанной по соответствующему статистическому методу эмпирической величины, так и найденных по соответствующим таблицам критических величин. Например, при подсчете рангового коэффициента корреляции Спирмена по таблице критических значений этого коэффициента были найдены следующие величины критических значений, которые для этого метода обозначаются греческой буквой ρ («ро»). Так для р = 0,05 по таблице найдена величина ρкр1 = 0,61 и для р = 0,01 величина ρкр2 = 0,76.
В принятой в дальнейшем изложении стандартной форме записи это выглядит следующим образом:
Теперь нам необходимо сравнить наше эмпирическое значение с двумя найденными по таблицам критическими значениями. Лучше всего это сделать, расположив все три числа на так называемой «оси значимости». «Ось значимости» представляет собой прямую, на левом конце которой располагается 0, хотя он, как правило, не отмечается на самой этой прямой, и слева направо идет увеличение числового ряда. По сути дела это привычная школьная ось абсцисс ОХ декартовой системы координат. Однако особенность этой оси в том, что на ней выделено три участка, «зоны». Одна крайняя зона называется зоной незначимости, вторая крайняя зона — зоной значимости, а промежуточная — зоной неопределенности. Границами всех трех зон являются Чкр1 для р = 0,05 и Чкр2 для р = 0,01, как это показано на рисунке.
В зависимости от правила принятия решения (правила вывода), предписанного в данном статистическом методе возможно два варианта.
Первый вариант: альтернативная гипотеза принимается, если Чэмп ≥ Чкр.
| Зона неопределенности |
| Зона незначимости |
| Зона значимости |
| 0,05 |
| 0,01 |
| Чкр1 |
| Чкр2 |
Или второй вариант: альтернативная гипотеза принимается, если Чэмп ≤ Чкр.
| Зона неопределенности |
| Зона значимости |
| Зона незначимости |
| 0,05 |
| 0,01 |
| Чкр1 |
| Чкр2 |
Подсчитанное Чэмп по какому либо статистическому методу должно обязательно попасть в одну из трех зон.
Если эмпирическое значение попадает в зону незначимости, то принимается гипотеза Н0 об отсутствии различий.
Если Чэмп попало в зону значимости, принимается альтернативная гипотеза Н1оналичии различий, а гипотеза Н0 отклоняется.
Если Чэмп попадает в зону неопределенности, перед исследователем стоит дилемма. Так, в зависимости от важности решаемой задачи он может считать полученную статистическую оценку достоверной на уровне 5%, и принять, тем самым гипотезу Н1, отклонив гипотезу Н0, либо — недостоверной на уровне 1%, приняв тем самым, гипотезу Н0. Подчеркнем, однако, что это именно тот случай, когда психолог может допустить ошибки первого или второго рода. Как уже говорилось выше, в этих обстоятельствах лучше всего увеличить объем выборки.
Подчеркнем также, что величина Чэмп может точно совпасть либо с Чкр1 либо Чкр2. В первом случае можно считать, что оценка достоверна точно на уровне в 5% и принять гипотезу Н1, или, напротив, принять гипотезу Н0. Во втором случае, как правило, принимается альтернативная гипотеза Н1 о наличии различий, а гипотеза Н0 отклоняется.
Проверка статистических гипотез
п.1. Понятие о статистической гипотезе
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| \(H_0\) | \(H_1\) | ||
| Принятая гипотеза | \(H_0\) | True Negative \(H_0\) принята верно | False Negative \(H_0\) принята неверно Ошибка 2-го рода |
| \(H_1\) | False Positive \(H_0\) отвергнута неверно \(H_1\) принята неверно Ошибка 1-го рода | True Positive \(H_0\) отвергнута верно \(H_1\) принята верно | |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Уровень значимости при проверке гипотезы
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости \(p\) | Решение о гипотезе \(H_0\) | Вывод для гипотезы \(H_1\) |
| \(p\gt 0,1\) | \(H_0\) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| \(0,5\lt p\leq 0,1\) | Истинность \(H_0\) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| \(0,01\lt p\leq 0,05\) | Отклонение \(H_0\), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| \(p\leq 0,01\) | Отклонение \(H_0\), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы \(H_1\).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с \(n\geq 100\) критический уровень снижают до α=0,01.
п.3. Критическая область
Различают 3 вида критических областей
п.4. Простая гипотеза и критерии согласия
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
\(H_0\): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
п.5. Критерий согласия \(X^2\) Пирсона
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| \(m_i\) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| \(f_i-m_i\) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| \(\frac<(f_i-m_i)^2> | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| \(m_i\) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| \(f_i-m_i\) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| \(\frac<(f_i-m_i)^2> | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(p_i\) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: \(X_e^2=36,84\)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для \(X_<кр>^2=X^2(\alpha,k-2)\).
Для уровня значимости α=0,05 и k=8, r=1 находим:
\(X_<кр>^2\approx 12,59\)
Получается, что: \(X_e^2\gt X_<кр>^2\)
Гипотеза \(H_0\) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x= <4;5;6;7>с редким числом попаданий:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 8 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 35 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(p_i\) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: \(X_e^2=1,12\)
Критическое значение статистики ищем в виде \(X_<кр>^2=X^2(\alpha,k-2)\), где α=0,05 и k=5, r=1
\(X_<кр>^2\approx 7,81\)
Получается, что: \(X_e^2\lt X_<кр>^2\)
Гипотеза \(H_0\) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики \(X_e^2\) в Примере 2, основной вклад внесло слагаемое для \(x_i=7\). Оно равно 34,34 и поэтому сумма \(X_e^2=36,84\) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты \(x_i=4,375\) слагаемое статистики равно 0,16 и сумма \(X_e^2=1,12\) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Уровни статистической значимости
Результаты математической обработки данных почти любым методом в конечном итоге оцениваются по уровню статистической значимости полученного результата. Это может быть уровень значимости коэффициента корреляции (Пирсона, Спирмена), уровень значимости различий по результатам сравнения выборок по тому или иному статистическому критерию (Стьюдента, Манна-Уитни, Вилкоксона, Хи-квадрат) и т.п. — вне зависимости от используемого метода, уровни значимости оцениваются одинаково.
Уровень статистической значимости обозначается латинской буквой p. Традиционно выделяют три уровня статистической значимости результатов математической обработки данных:
Кроме того, иногда в результатах исследований выделяют и описывают также близкие к статистически значимым результаты (p≈0,05). Сюда можно отнести такие показатели статистической значимости, как 0,06, 0,07, 0,08 и 0,09. Они свидетельствуют о наличии тенденции к существованию соответствующей закономерности.
Что касается показателей статистической значимости величиной от 0,1 и выше — они говорят о том, что полученный результат не является статистически значимым. Например, если речь идет о сравнении выборок, то подобный показатель свидетельствует об отсутствии статистически значимых различий между сравниваемыми выборками.
По сути уровень статистической значимости отражает вероятность ошибки в выявлении закономерности. Поэтому чем меньше величина показателя p, тем ниже вероятность ошибки, тем более статистически значимым является полученный результат.
Уровень статистической значимости (р)
В таблицах результатов статистических расчётов в курсовых, дипломных и магистерских работах по психологии всегда присутствует показатель «р».
Например, в соответствии с задачами исследования были рассчитаны различия уровня осмысленности жизни у мальчиков и девочек подросткового возраста.
Уровень статистической значимости (p)
В правом столбце указано значение «р» и именно по его величине можно определить значимы различия осмысленности жизни в будущем у мальчиков и девочек или не значимы. Правило простое:
Откуда берется уровень статистической значимости «р»
Уровень статистической значимости вычисляется статистической программой вместе с расчётом статистического критерия. В этих программах можно также задать критическую границу уровня статистической значимости и соответствующие показатели будут выделяться программой.
Например, в программе STATISTICA при расчете корреляций можно установить границу «р», например, 0,05 и все статистически значимые взаимосвязи будут выделены красным цветом.
Если расчёт статистического критерия проводится вручную, то уровень значимости «р» выявляется путем сравнения значения полученного критерия с критическим значением.
Что показывает уровень статистической значимости «р»
Все статистические расчеты носят приблизительный характер. Уровень этой приблизительности и определяет «р». Уровень значимости записывается в виде десятичных дробей, например, 0,023 или 0,965. Если умножить такое число на 100, то получим показатель р в процентах: 2,3% и 96,5%. Эти проценты отражают вероятность ошибочности нашего предположения о взаимосвязи, например, между агрессивностью и тревожностью.
То есть, коэффициент корреляции 0,58 между агрессивностью и тревожностью получен при уровне статистической значимости 0,05 или вероятности ошибки 5%. Что это конкретно означает?
Выявленная нами корреляция означает, что в нашей выборке наблюдается такая закономерность: чем выше агрессивность, тем выше тревожность. То есть, если мы возьмем двух подростков, и у одного тревожность будет выше, чем у другого, то, зная о положительной корреляции, мы можем утверждать, что у этого подростка и агрессивность будет выше. Но так как в статистике все приблизительно, то, утверждая это, мы допускаем, что можем ошибиться, причем вероятность ошибки 5%. То есть, сделав 20 таких сравнений в этой группе подростков, мы можем 1 раз ошибиться с прогнозом об уровне агрессивности, зная тревожность.
Какой уровень статистической значимости лучше: 0,01 или 0,05
Уровень статистической значимости отражает вероятность ошибки. Следовательно, результат при р=0,01 более точный, чем при р=0,05.
В психологических исследованиях приняты два допустимых уровня статистической значимости результатов:
р=0,01 – высокая достоверность результата сравнительного анализа или анализа взаимосвязей;
р=0,05 – достаточная точность.
Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать
Уровни значимости критерия
Уровень значимости – вероятность ошибочного отклонения (отвержения) гипотезы, в то время как она на самом деле верна. Речь идет об отклонении нулевой гипотезы.
1. 1-й уровень значимости: α ≤ 0,05.
Это 5%-ный уровень значимости. До 5% составляет вероятность того, что мы ошибочно сделали вывод о том, что различия достоверны, в то время как они недостоверны на самом деле. Можно сказать и по-другому: мы лишь на 95% уверены в том, что различия действительно достоверны.
2. 2-й уровень значимости: α ≤ 0,01.
Это 1%-ный уровень значимости. Вероятность ошибочного вывода о том, что различия достоверны, составляет не более 1%. Можно сказать и по-другому: мы на 99% уверены в том, что различия действительно достоверны.
3. 3-й уровень значимости: α ≤ 0,001.
В области ФК и спорта достаточен уровень значимости α = 0,05, более серьезные выводы рекомендуется давать, используя уровень значимости α = 0,01 или α = 0,001.
7.2. F- критерий Фишера
Пример 4. В экспериментальной группе школьников средний прирост результатов в прыжках в длину с разбега, после применения новой методики обучения, составил 10 см ( 

Экспериментальная группа (xi): 17; 11; 3; 8; 9; 12; 10; 13; 10; 7.
Контрольная группа (yi): 8; 1; 6; 2; 3; 0; 4; 7; 5; 4.
Можно ли утверждать, что нововведения эффективнее повлияли на процесс формирования изучаемого двигательного действия по сравнению с традиционной методикой?
1) Задаемся уровнем значимости α = 0,05.
2) Вычисляем исправленные выборочные дисперсии из нашего примера по формуле:
4) Из таблицы 3 приложения при α =0,05; df1 = n1 – 1 = 9; df2 = n2 – 1 = 9; находим F0,05 = 3,18
5) Сравниваем между собой значения F и F0,05.
Вывод. Поскольку F
Общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. t-статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмещенной оценки дисперсии.
Устанавливает доказательство достоверного различия или, наоборот, отсутствие различия в двух выборочных средних значениях для независимых выборок. Рассмотрим последовательность вычислений, используя пример 4:
1) Принимаем предположение о нормальности распределения генеральных совокупностей, из которых получены данные. Формулируем гипотезы:
Нулевая гипотеза Ho: 

Альтернативная гипотеза: H1: 

Задаемся уровнем значимости α = 0,05.
2) В результате предварительной проверки при использовании критерия Фишера установлено, что различие дисперсий статистически недостоверно: D(x) = D(y).
3) Так как генеральные дисперсии D(x) и D(y) одинаковы, а n1 и n2 – объёмы малых независимых выборок, то наблюдаемое значение критерия равно:
Вычисляем число степеней свободы по формуле
Нулевая гипотеза отвергается, если │ 



Вывод: поскольку 

Таким образом, нововведения успешнее решают задачу обучения школьников прыжкам в длину с разбега, чем традиционная методика.
Далее рассмотрим сравнение двух выборочных средних значений для связанных выборок (парное сравнение).
Условия применения 

Пример 5. Группа 10 школьников в течение летних каникул находилась в летнем оздоровительном лагере. До и после сезона у них измеряли жизненную емкость легких (ЖЕЛ). По результатам измерений нужно определить, достоверно ли изменился этот показатель под влиянием физических упражнений на свежем воздухе.
Исходные данные до эксперимента (xi; мл) 3400; 3600; 3000; 3500; 2900; 3100; 3200; 3400; 3200; 3400, т.е. объем выборки n = 10.
После эксперимента (yi; мл): 3800; 3700; 3300; 3600; 3100; 3200; 3200; 3300; 3500; 3600.
1) Находим разность связанных пар результатов измерения di:

2) Формулируем гипотезы:
Нулевая гипотеза Ho: 
Альтернативная гипотеза: H1: 
3) Задаемся уровнем значимости α = 0,05
5) Значение t- критерия определяем по формуле для связанных пар:
Из таблицы 1 приложения находим критическое значение t – критерия при α = 0,05; 

Вывод:Поскольку t > tкр (3,36 > 2,262)наблюдаемое различие по показателю ЖЕЛ является статистически достоверным на уровне значимости α=0,05.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Афанасьев В.В. Основы отбора, за и контроля в спорте / В.В. Афанасьев, А.В. Муравьев, И.А. Осетров. – Ярославль: Изд-во ЯГПУ, 2008. − 278 с.
2. Биленко, А.Г. Основы спортивной метрологии: Учебное пособие /А.Г. Биленко, Л.П. Говорков; СПб ГУФК им. П.Ф. Лесгафта. – СПб., 2005. – 138 с.
3. Губа В.П. Измерения и вычисления в спортивно- педагогической практике: учебное пособие для студентов высших учебных заведений/ В.П. Губа, М.П.Шестаков, Н.Б. Бубнов, М.П. Борисенков. – М.: ФиС, 2006. – 220 с.
5. Коренберг, В.Б. Спортивная метрология: учебник / В.Б. Коренберг – М.: Физическая культура, 2008. – 368 с.
6. Начинская, С. В. Спортивная метрология. Учебное пособие для студ. высш. учеб. заведений / С. В. Начинская.– М.: Издательский центр «Академия», 2005. – 240 с.
7. Начинская С.В. Применение статистических методов в сфере физической культуры / Начинская С.В – СПб., 2000. – 260 с.
8. Смирнов, Ю. И. Спортивная метрология: учеб. для студ. пед. вузов / Ю. И Смирнов, М. М. Полевщиков. – М.: Издат. центр «Академия», 2000. – 232 с.