что означает символ o в теории алгоритмов

«O» большое и «o» малое

«O» большое и «o» малое ( и ) — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также в информатике и теории алгоритмов.

Содержание

Определения

Пусть и — две функции, определенные в некоторой проколотой окрестности точки , причем в этой окрестности не обращается в ноль. Говорят, что:

Иначе говоря, в первом случае отношение в окрестности точки ограничено сверху, а во втором оно стремится к нулю при .

Обозначение

Обычно выражение «f является „O“ большим („о“ малым) от g» записывается с помощью равенства f(x) = O(g(x)) (соответственно, f(x) = o(g(x))).

Это обозначение очень удобно, но требует некоторой осторожности при использовании (а потому в наиболее элементарных учебниках его могут избегать). Дело в том, что это не равенство в обычном смысле, а несимметричное отношение.

В частности, можно писать

Другой пример: при x → 0 верно, что

Вместо знака равенства методологически правильнее было бы употреблять знаки принадлежности и включения, понимая O( ) и o( ) как обозначения для множеств функций, то есть, используя запись в форме

Однако на практике такая запись встречается крайне редко, в основном, в простейших случаях.

При использовании данных обозначений должно быть явно оговорено (или очевидно из контекста), о каких окрестностях (одно- или двусторонних; содержащих целые, вещественные или комплексные числа и т. п.) и о каких допустимых множествах функций идет речь (поскольку такие же обозначения употребляются и применительно к функциям многих переменных, к функциям комплексной переменной, к матрицам и др.).

Другие подобные обозначения

Для функций f(n) и g(n) при n → n₀ используются следующие обозначения:

где U — проколотая окрестность точки n₀.

Основные свойства

Транзитивность

Рефлексивность

Симметричность

Перестановочная симметрия

Другие

Асимптотические обозначения в уравнениях

Приведенная интерпретация подразумевает выполнение соотношения:

, где A, B, C — выражения, которые могут содержать асимптотические обозначения.

Примеры использования

История

Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом (англ.) во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. Обозначение «„о“ малое» впервые использовано другим немецким математиком, Эдмундом Ландау в 1909 году; с работами последнего связана и популяризация обоих обозначений, в связи с чем их также называют символами Ландау. Обозначение пошло от немецкого слова «Ordnung» (порядок).

Источник

Оценка сложности алгоритмов, или Что такое О(log n)

Авторизуйтесь

Оценка сложности алгоритмов, или Что такое О(log n)

Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.

Оценка сложности

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.

Примеры

O(n) — линейная сложность

Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.

O(log n) — логарифмическая сложность

Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.

O(n 2 ) — квадратичная сложность

Бывают и другие оценки по сложности, но все они основаны на том же принципе.

Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.

Наглядно

Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:

Тут можно посмотреть сложность основных алгоритмов сортировки и работы с данными.

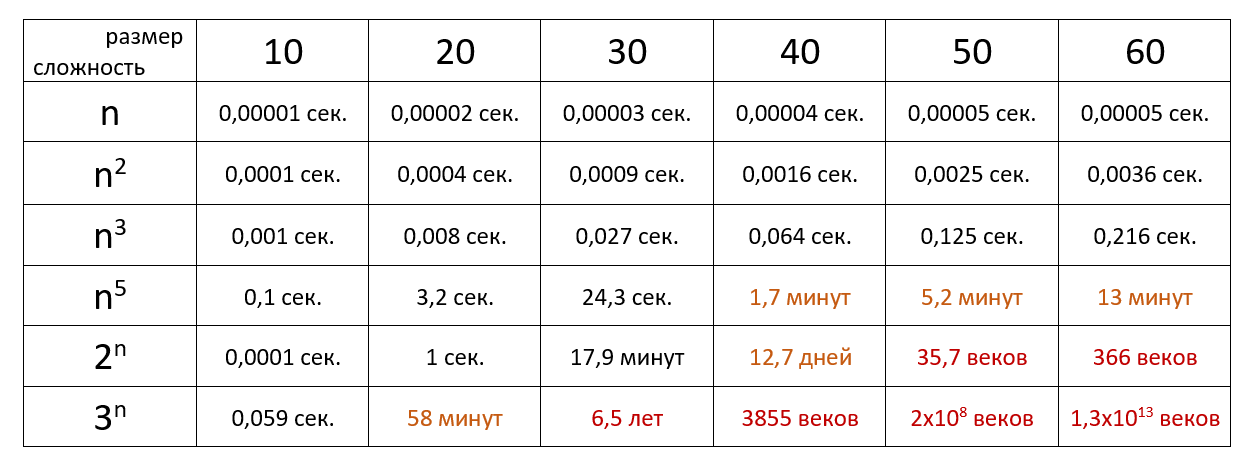
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».

Источник

Сложность алгоритмов. Big O. Основы.

Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.

Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.

Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.

Распространённые сложности алгоритмов

Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.

Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.

Пример № 1.

У нас есть массив из 5 чисел и нам надо получить первый элемент.

Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.

Пример № 2.

Сложение двух чисел. Функция всегда выполняет константное количество операций.

Пример № 3.

Размер массива. Опять же, функция всегда выполняет константной количество операций.

Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.

Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.

Пример № 3.

Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.

К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.

Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.

Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.

Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.

Такие алгоритмы легко узнать по вложенным циклам.

Пример № 1.

В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )

Зачем изучать Big O

Шпаргалка

Небольшие подсказки, которые помогут определить сложность алгоритма.

Полезные ссылки

Источник

«O» большое и «o» малое

Содержание

Определения

Пусть f(x) и g(x) — две функции, определенные в некоторой проколотой окрестности точки x₀, причем в этой окрестности g не обращается в ноль. Говорят, что:

Иначе говоря, в первом случае отношение |f|/|g| в окрестности точки x₀ ограничено сверху, а во втором оно стремится к нулю.

Обозначение

«f является „O“ большим („о“ малым) от g»

Это обозначение очень удобно, но требует некоторой осторожности при использовании (а потому в наиболее элементарных учебниках его могут избегать). Дело в том, что это не равенство в обычном смысле, а несимметричное отношение

«если функция такова, как написано слева от знака равенства, то она и такова, как записано справа»:

в частности, можно писать

бессмысленны. Другой пример: при x → 0 верно, что

Вместо знака равенства методологически правильнее было бы употреблять знаки принадлежности и включения, понимая O( ) и o( ) как обозначения для множеств функций, то есть используя запись в форме

Однако на практике такая запись встречается крайне редко, в основном в простейших случаях.

При использовании данных обозначений должно быть явно оговорено (или очевидно из контекста), о каких окрестностях (одно- или двусторонних; содержащих целые, вещественные или комплексные числа и т. п.) и о каких допустимых множествах функций идет речь (поскольку такие же обозначения употребляются и применительно к функциям многих переменных, к функциям комплексной переменной, к матрицам и др.).

Основные свойства

Примеры использования

Другие подобные обозначения

Реже используются обозначения:

История

Обозначение «„O“ большое» введено немецким математиком Паулем Бахманом (Paul Gustav Heinrich Bachmann) во втором томе его книги «Analytische Zahlentheorie» (Аналитическая теория чисел), вышедшем в 1894 году. Обозначение «„о“ малое» впервые использовано другим немецким математиком, Эдмундом Ландау (Edmund Georg Hermann Landau) в 1909 году; с работами последнего связана и популяризация обоих обозначений, в связи с чем их также называют символами Ландау. pl:Notacja dużego O sr:Велико О sv:Ordo th:สัญกรณ์โอใหญ่ uk:Нотація Ландау

Источник

Асимптотический анализ алгоритмов

Прежде чем приступать к обзору асимптотического анализа алгоритмов, хочу сказать пару слов о том, в каких случаях написанное здесь будет актуальным. Наверное многие программисты читая эти строки, думают про себя о том, что они всю жизнь прекрасно обходились без всего этого и конечно же в этих словах есть доля правды, но если встанет вопрос о доказательстве эффективности или наоборот неэффективности какого-либо кода, то без формального анализа уже не обойтись, а в серьезных проектах, такая потребность возникает регулярно.
В этой статье я попытаюсь простым и понятным языком объяснить, что же такое сложность алгоритмов и асимптотический анализ, а также возможности применения этого инструмента, для написания собственного эффективного кода. Конечно, в одном коротком посте не возможно охватить полностью такую обширную тему даже на поверхностном уровне, которого я стремился придерживаться, поэтому если то, что здесь написано вам понравится, я с удовольствием продолжу публикации на эту тему.

Во многих работах описывающих те или иные алгоритмы, часто можно встретить обозначения типа:
O(g(n)), &#937(g(n)), &#920(g(n)).
Давайте разбермся, что же это такое, но сначала я перечислю основные классы сложности применяемые при анализе:
f(n) = O(1) константа
f(n) = O(log(n)) логарифмический рост
f(n) = O(n) линейный рост
f(n) = O(n*log(n)) квазилинейный рост
f(n) = O(n^m) полиномиальный рост
f(n) = O(2^n) экспоненциальный рост

Если раньше вы не встречались с подобными обозначениями, не переживайте, после прочтения этой статьи, все станет намного понятнее.
А начнем мы с символа O.

Сначала приведу формальное определение:
(1.1) Запись вида f(n) = O(g(n)) означает, что ф-ия f(n) возрастает медленнее чем ф-ия g(n) при с = с1 и n = N, где c1 и N могут быть сколь угодно большими числами, т.е. При c = c1 и n >= N, c*g(n) >=f(n).
Таким образом O – означает верхнее ограничение сложности алгоритма.

Давайте теперь попробуем применить это знание на практике.

Возьмем известную любому программисту задачу сортировки. Допустим нам необходимо отсортировать массив чисел, размерностью 10 000 000 элементов. Договоримся рассматривать худший случай, при котором для выполнения алгоритма понадобится наибольшее количество итераций. Не долго думая, мы решаем применять сортировку пузырьком как самую простую с точки зрения реализации.
Сортировка пузырьком позволяет отсортировать массив любой размерности без дополнительных выделений памяти. Вроде бы все прекрасно и мы с чистой совестью начинаем писать код (для примеров здесь и далее будет использоваться язык Python).

рис.1.
зеленая кривая соответствует графику ф-ии x^2 при c = 1, синия c = 5, красная c = 7

Здесь и далее на всех графиках ось абсцисс будет соответствовать размерности входных данных, а ось ординат кол-ву итераций необходимых для выполнения алгоритма.
Нас интересует только та часть координатной плоскости, которая соответствует значениям x большим 0, т.к. любой массив, по-определению, не может иметь отрицательный размер, поэтому, для удобства, уберем левые части графиков ф-ий, ограничившись лишь первой четвертью координатной плоскости.

рис.2.
зеленая кривая соответствует графику ф-ии x^2 при c = 1, синия c = 5, красная c = 7

Возьмем c2 = 7. Мы видим, что новая ф-ия растет быстрее предыдущей (красная кривая на рис.2). Из определения (1.1), делаем вывод, что при с2 = 7 и n >= 0, g(n) = 7*n^2 всегда больше или равна ф-ии f(n) = 5*n^2, следовательно наша программа имет сложность O(n^2).
Кто не до конца понял это объяснение, посмотрите на графики ф-ий и заметьте, что ф-ия отмеченная на нем красным, при n >= 0 всегда имеет большее значение по y, чем ф-ия отмеченная синим.

Что же можно сделать в этой ситуации, чтобы радикально ускорить сортировку? Необходимо, чтобы в худшем случае сложность алгоритма была меньше чем O(n^2). Поразмыслив немного, мы решаем, что не плохо бы было, придумать такой алгоритм, сложность которого не превышает O(n), т.е. является линейной. Очевидно, что в случае O(n) скорость работы программы возрастет в N раз, так как вместо N^2 итераций, нам необходимо будет сделать всего лишь N. Прогнозируемый прирост скорости отлично виден на рис.3.

Серой прямой обозначена линейная сложность, а три кривых показывают сложность n^2 при различных коэффициентах c.

Но оказывается, что сделать сортировку со сложностью O(n) в общем случае просто не возможно (док-во)! Так на какую же сложность мы в лучшем случае можем расчитывать? Она равна O(n*log(n)), что является теоретически доказаным минимальным верхнем пределом для любого алгоритма сортировки основанного на сравнении элементов. Это конечно немного не то, чего мы ожидали получить, но все же это уже и не O(n^2). Осталось найти алгоритм сортировки удовлетворяющий нашим требованиям.
Покопавшись в интернете, видим, что им удовлетворяет «пирамидальная сортировка». Я не буду вдаваться в подробности алгоритма, желающие могут прочитать о нем самостоятельно на wiki, скажу только, что его сложность принадлежит классу O(n*log(n)) (т.е. максимально возможная производительность для сортировки), но при этом, он довольно труден в реализации.

Посмотрим на графики ниже и сравним скорости возрастания кол-ва вычислений для двух рассмотренных алгоритмов сортировки.

рис.4.

Фиолетовая кривая показывает алгоритм со сложностью n*log(n). Видно, что на больших n, пирамидальная сортировка существенно выигрывает у сортировки пузырьком при любом из трех опробованных нами коэффициентах, однако все-равно уступает гипотетической сортировке линейной сложности (серая прямая на графике).
В любом случае, даже на медленном компьютере она будет работать гораздо быстрее, чем «пузырек» на быстром.

Остается открытым вопрос, целесообразно ли всегда предпочитать пирамидальную сортировку сортировке пузырьком?

рис.5.

Как видно на рис.5, при малых n, различия между двумя алгоритмами достаточно малы и выгода от использования пирамидальной сортировки — совсем незначительна, а учитывая, что «пузырек» реализуется буквально 5-6 строчками кода, то при малых n, он действительно является более предпочтительным с точки зрения умственных и временных затрат на реализацию 🙂

В заключении, чтобы более наглядно продемонстрировать разницу между классами сложности, приведу такой пример:
Допустим у нас етсь ЭВМ 45-ти летней давности. В голове сразу всплывают мысли о больших шкафах, занимающих довольно-таки обширную площадь. Допустим, что каждая команда на такой машине выполняется примерно за 10 миллисек. С такой скоростью вычислений, имея алгоритм сложности O(n^2), на решение поставленой задачи уйдет оооочень много времени и от затеи придется отказаться как от невыполнимой за допустимое время, если же взять алгоритм со сложностью O(n*log(n)), то ситуация в корне изменится и на расчет уйдет не больше месяца.

Посчитаем, сколько именно займет сортировка массива в обоих случаях

сверх-неоптимальный алгоритм (бывает и такое, но редко):
O(2^n) = оооооочень медленно, вселенная умрет, прежде чем мы закончим наш расчет…
пузырек:
O(n^2) = 277777778 часов (классический “пузырек”)
пирамидальная сортировка:
O(n*log(n)) = 647 часов (то чего мы реально можем добиться, применяя пирамидальную сортировку)
фантастически-эффективный алгоритм:
O(n) = 2.7 часов (наш гипотетический алгоритм, сортирующий за линейное время)
и наконец:
O(log(n)) = оооооочень быстро, жаль, что чудес не бывает…

Два последних случая (хоть они и не возможны в реальности при сортировке данных) я привел лишь для того, чтобы читатель ощутил огромную разницу между алгоритмами различных классов сложности.
На последок хочу заметить, что буквой O обычно обозначают минимальный из классов сложности, которому соответствует данный алгоритм. К примеру, я мог бы сказать, что сложность сортировки пузырьком равна O(2^n) и теоретически это было бы абсолютно верным утверждением, однако на практике такая оценка была бы лишена смысла.

Источник