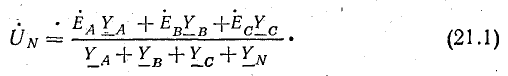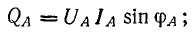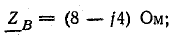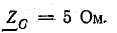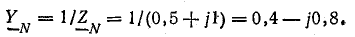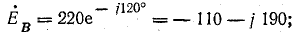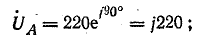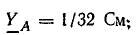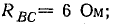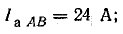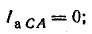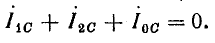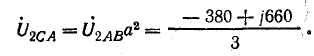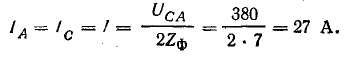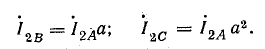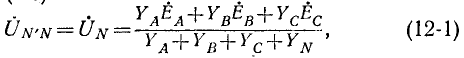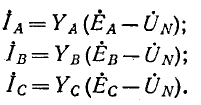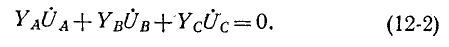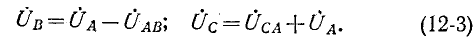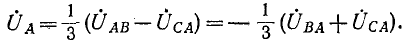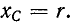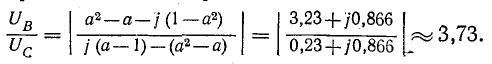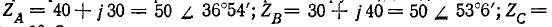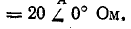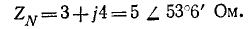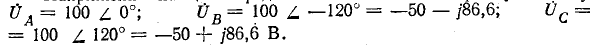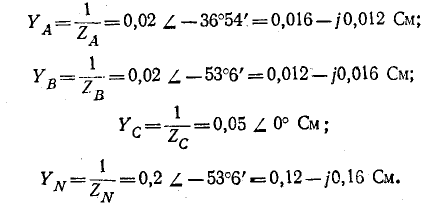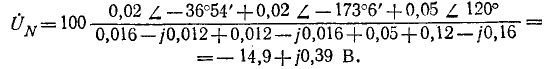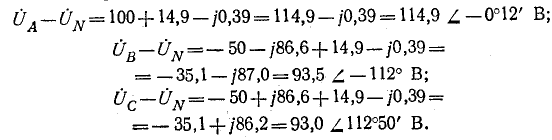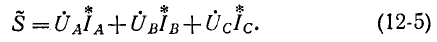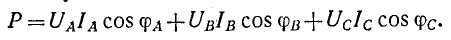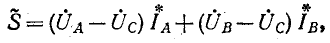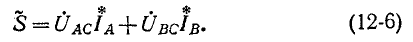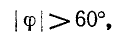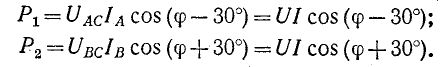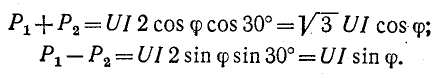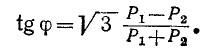что означает смещение нейтрали

Напряжение смещения нейтрали в трехфазных цепях

Как уже писалось (например, здесь) нейтралью называют общую точку обмоток электрических машин при соединении в схему звезда, при соединении в схему треугольник для получения нейтральной точки можно использовать схему “скользящий треугольник”.

Синонимом понятия “смещение нейтрали” является выражение “перекос фаз”. Оба эти словосочетания используются в лексиконе и профессиональной среде электриков.

В данной статье будем рассматривать смещение нейтрали у нагрузки. Для начала выведем формулу для расчета напряжения смещения нейтрали, для этого нарисуем схему замещения трехфазной сети, где в обычном режиме напряжения фаз представляют собой синусоиды, которые при равномерной нагрузке фаз сдвинуты на 1200 и в любой момент времени их сумма равна 0. В нашем же случае, нагрузка будет неравномерная, что приведет к смещению нейтрали, что можно увидеть по рисунку с векторными диаграммами.

Напряжение смещения нейтрали определяется по следующей формуле:

Под смещением нейтрали понимают, что между нулевым проводом источника и нагрузки возникает напряжение, а по нулевому проводу течет ток. Но, это в случае, если нулевые провода соединены. Если же нулевой провод источника и нагрузки не соединен, то смещение нейтрали может вызвать нарушение магнитного равновесия в трансформаторе.

Идеальный случай (симметричная нагрузка), при котором смещения нейтрали не происходит, сумма напряжений в любой момент времени равна нулю, линейные трех фаз составляют

При данном стечении обстоятельств, происходит смещение нейтрали, которому соответствует отрезок 00’ на рисунке сверху слева, который и создает ток в нулевом проводе. Смещения в ту или иную сторону точки 0’ от точки 0 будет зависеть от характера нагрузки. В данном примере нагрузка однородная, но неравномерная, различающаяся по величине, но не по типу.

В случае с разнородной неравномерной нагрузкой нейтральная точка нагрузки (0’) вышла за пределы треугольника. Значения же фазных напряжений на нагрузке превышают это значение на источнике питания в несколько раз. Однако, не следует забывать, что это смещение происходит только на нагрузке, а не на источнике питания.

Неоднородность нагрузки будет влиять на источник питания (трансформатор или генератор), только, если относительно источника эта нагрузка будет велика. В этом случае может произойти нарушение магнитной устойчивости трансформатора.

Следует помнить, чем выше нагрузка, тем большее влияние на систему она может оказывать, аналогично, как большие двигатели серьезнее просаживают напряжение на шинах при перерывах питания на электростанциях.

Источник

Перекос фаз, расфазовка или – смещение нейтрали

Для тех, кто еще не знает, открою истину, а другим напомню, что ток передается от электростанции к потребителю по трем фазам через повышающие трансформаторы напряжения и нулевой провод в этом случае не используется. А вот после того, как напряжение понижается и приходит к потребителю мы к этим трем фазам получаем и такое счастье, как нулевой провод. Когда внезапно пропадает контакт между нулем понижающего трансформатора (со станции, подстанции, ВРУ и т.д. и т.п.) и нулевым проводом в электрическом стояке возникает такое явление, которое называется смещением нейтрали. Напряжения в фазах сдвинуты друг относительно друга на угол 120°. Очень часто не сильно грамотные электрики называют это перекосом фаз, но на самом деле перекос фаз означает изменение угла между фазами вследствие несимметричности нагрузки, что сделать крайне нереально. Даже несимметричная нагрузка может привести лишь к тому, что вы не сможете использовать вашу электросеть с полной нагрузкой. Предположим, есть три фазы с максимальным значением 16 ампер. Вы всю свою нагрузку подключили к одной фазе, вместо возможных 10,5 кВт вы получите только 3,5 кВт. Но абсолютно ничего страшного в этом нет.

Теперь о «расфазовке». Этот термин используют совсем неграмотные электрики. У фаз существует порядок АВС. Этот порядок важен только на этапе монтажа и проектирования. Важность его заключается в том, что трехфазные двигатели вращаются вправо или влево, как раз, вследствие изменения чередования фаз. Так что под сленгом «расфазовка» (такого термина вообще не существует) правильнее будет использовать термин — порядок чередования фаз.

Смещение нейтрали

Ну вот, с терминами разобрались, осталось узнать, что такое смещение нейтрали, каковы признаки и как оно возникает.

Так выглядит треугольник-звезда напряжений в исправной электросети. Между вершинами треугольника, то есть между фазами напряжение 380 вольт и это напряжение называется линейным. А вот между любой фазой и нулем, привычное нам, напряжение 220 вольт и оно называется фазным.

Снова немного окунемся в теорию. В трехфазной сети есть такая особенность, что по нулевому проводу ток максимальный в том случае, если загружена ТОЛЬКО одна фаза. При симметричной нагрузке всех трех фаз ток в нулевом проводе равен нулю.

Итак, в подъезд подается три фазы, дальше фазы в определенном порядке подаются в разные квартиры с целью хотя бы приблизительно обеспечить симметрию нагрузки, а вот ноль идет абсолютно во все квартиры. Схематично и упрощенно это можно представить в виде трех розеток.

А теперь представьте себе, что автомат защиты выбран неправильно, нагрузка несимметрична и по нулевому проводу начинает протекать очень большой ток, который вызывает нагрев провода. В конце концов, ноль отгорает. Или ноль после ремонтных работ электрик по своей халатности забывает присоединить на место.

Дальше, в любую розетку мы включим лампочку, но две других трогать не будем.

И ничего не произойдет. В том плане, что лампочка не загорится. Она попросту будет кусочком провода, который соединит фазу «А» с бывшим нулевым проводом и бывший нулевой провод просто станет продолжением фазы «А», но только подключенным через лампочку. Теперь посмотрим, что будет на диаграмме:

А видим мы следующее, что теперь между бывшим нулевым проводом и двумя другими фазами («С» и «В») будет напряжение 380 вольт. Включаем еще одну точно такую же лампочку в другую розетку.

Теперь между бывшим нулевым проводом и каждой из фаз «А» или «В» напряжение будет около 190-200 вольт, а фазой «С» около 360 вольт.

Ну и в завершении, если мы включим еще одну такую же лампочку в третью розетку, мы снова получим диаграмму, как на самом верхнем рисунке.

Делаем выводы. Чем больше нагрузка в фазе при обрыве нулевого провода, тем сильнее падает напряжение в этой фазе, но возрастает в других. Угадать, что будет через секунду в такой сети просто нереально. Очень хорошо видно, что нулевая точка смещается относительно фазных проводников и относительно нулевой точки, как таковой, и именно поэтому такое явление называется – смещением нейтрали. Говорить о перекосе фаз в этом случае тоже не получается, фазы остаются на месте, напряжение между ними неизменно, угол сдвига фаз равен 120° — изменяется потенциал (напряжение) нулевого провода относительно фаз и относительно нулевой точки понижающего трансформатора. «Расфазировки» тоже не происходит – порядок фаз не меняется. Но что в этом случае страшно, это короткое замыкание одной из фаз. Если при включении-выключении приборов ноль просто гуляет, нагрузка более или менее равномерна, то при коротком замыкании (якобы коротком, потому что ноль оборван) на одной фазе, на двух соседних напряжение сразу поднимется минимум до 360 вольт, а максимум до 400. При целом нулевом проводе и надежном контакте смещение нейтрали тоже происходит, но в пределах 1-3%. При большой несимметричности нагрузки всё, что может произойти это просадка напряжения в одной из фаз, просто потому, что проводник фазы не справляется с нагрузкой и происходит очень небольшое смещение нейтрали, но напряжение в соседних фазах при этом если и повысится, то на 1-5 вольт, не больше. Так что, если в вашем доме начали перегорать лампочки, бытовые приборы и другое электрооборудование по вечерам или утрам, или наоборот, вы не можете пользоваться бытовыми приборами из-за нехватки напряжения, запросто может оказаться, что оборвался нулевой провод на электрическом стояке. Запомните одну простую вещь, на смещение нейтрали указывает понижение напряжения на одной (двух фазах), но при этом на соседних двух (одной – соответственно) фазах напряжение ЗНАЧИТЕЛЬНО ПОВЫШАЕТСЯ. Выражаясь техническим языком: нейтральный провод обеспечивает СИММЕТРИЮ фазных напряжений при НЕСИММЕТРИЧНОЙ нагрузке. Именно для этого делается перемычка на вводе между заземляющей и нулевой шинкой, чтобы снизить смещение нейтрали (Заземление нулевого провода). И именно поэтому рекомендуется выключать электроприборы из розеток, когда вы ими не пользуетесь, потому что никогда не угадаешь, когда произойдет обрыв нулевого провода. Чтобы защитить себя от последствий смещения нейтрали можно установить реле контроля напряжения, подробнее об этом можно почитать в этой статье.

Источник

Перекос фаз в трехфазной сети — чем опасен и когда возникает?

Самая распространенная проблема, порождающая массу деструктивных последствий – перекос фаз в трехфазной сети (до 1,0 кВ) с глухозаземленной нейтралью. При определенных условиях такое явление может вывести из строя электрические приборы и создать угрозу для жизни. Учитывая актуальность проблемы, будет полезным узнать, что представляет собой несимметрия токов и напряжений, а также причины ее возникновения. Это позволит выбрать наиболее оптимальную стратегию защиты.

Что такое перекос фаз?

Данный термин используется для описания состояния сети, при котором возникают неравномерные нагрузки между фазами, что приводит к возникновению перекоса. Если составить векторную диаграмму идеальной трехфазной сети, то она будет выглядеть так, как показано на рисунке ниже.

Диаграмма напряжений в идеальных трехфазных сетях

Как видно из рисунка, в данном случае равны как линейные напряжения (АВ=ВС=СА=380,0 В), так и фазные (АN=ВN=СN=220,0 В). К сожалению, на практике добиться такого идеального равенства нереально. То есть, линейные напряжения сети, как правило, совпадают, в то время как в фазных наблюдаются расхождения. В некоторых случаях они могут превысить допустимый предел, что приведет к возникновению аварийной ситуации.

Пример диаграммы напряжений при возникновении перекоса

Допустимые нормы значений перекоса

Поскольку в трехфазных сетях предотвратить и полностью устранить перекосы невозможно, существуют нормы несимметрии, в которых установлены допустимые отклонения. В первую очередь это ГОСТ 13109 97, ниже приведена вырезка из него (п. 5.5), чтобы избежать разночтения документа.

Нормы несимметрии напряжения ГОСТ 13109-97

Поскольку, основная причина перекоса фаз напрямую связана с неправильным распределением нагрузок, существуют нормы их соотношения, прописанные в СП 31 110. Вырезку из этого свода правил также приведем в оригинале.

Вырезка из СП 31-110 (п 9.5)

Здесь необходимы пояснения в терминологии. Для описания несимметрии используются три составляющих, это прямая, нулевая и обратная последовательность. Первая считается основной, она определяет номинальное напряжение. Две последние можно рассматривать в качестве помех, которые приводят к образованию в цепях нагрузки соответствующих ЭДС, которые не участвуют в полезной работе.

Причины перекоса фаз в трехфазной сети

Как уже упоминалось выше, данное состояние электросети чаще всего вызвано неравномерным подключением нагрузки на фазы и обрывом нуля. Чаще всего это проявляется в сетях до 1, кВ, что связано с особенностями распределения электроэнергии, между однофазными электроприемниками.

Обмотки трехфазных силовых трансформаторов подключаются «звездой». Из места соединения обмоток отводится четвертый провод, называемый нулевым или нейтралью. Если происходит обрыв нулевого провода, то в сети возникает несимметрия напряжений, причем перекос напрямую будет зависеть от текущей нагрузки. Пример такой ситуации приведен ниже. В данном случае R_Н это сопротивления нагрузок, одинаковые по значению.

Перекос фаз, вызванный обрывом нейтрали

В данном примере напряжение на нагрузке, подключенной к фазе А, превысит норму и будет стремиться к линейному, а на фазе С упадет ниже допустимого предела. К подобной ситуации может привести перекос нагрузки, выше установленной нормы. В таком случае напряжение на недогруженных фазах повысится, а на перегруженных упадет.

К перекосу напряжений также приводит работа сети в неполнофазном режиме, когда происходит замыкание фазного провода на землю. В аварийных ситуациях допускается эксплуатация сети в таком режиме, чтобы обеспечить электроснабжение потребителям.

Исходя из вышесказанного, можно констатировать три основные причины перекоса фаз:

Несимметрия в высоковольтных сетях

Вызвать подобное состояние в сети 6,0-10,0 кВ иногда может подключенное к ней оборудование, в качестве характерного примера можно привести дугоплавильную печь. Несмотря на то, что она не относится к однофазному оборудованию, управление тока дуги в ней производится пофазно. В процессе плавки также могут возникнуть несимметричные КЗ. Учитывая, что существуют дугоплавильные установки запитывающиеся от напряжения 330,0 кВ, то можно констатировать, что и в данных сетях возможен перекос фаз.

В высоковольтных сетях перекос фаз может быть вызван конструктивными особенностями ЛЭП, а именно, разным сопротивлением в фазах. Чтобы исправить ситуацию выполняется транспозиция фазных линий, для этого устанавливаются специальные опоры. Эти дорогостоящие сооружения не отличаются особой прочностью. Такие опоры не особо стремятся устанавливать, предпочитая пожертвовать качеством электроэнергии, чем надежностью ЛЭП.

Опасность и последствия

Считается, что наиболее значимые последствия несимметрии связаны с низким качеством электроэнергии. Это, безусловно, так, но нельзя забывать и о других негативных воздействиях. К таковым относится образование уравнительных токов, вызывающих увеличение расхода электрической энергии. В случае с трехфазным автономным электрическим генератором это также приводит к повышенному расходу дизеля или бензина.

При равномерном подключении нагрузки, геометрическая сумма проходящих через нее токов была бы близкой к нулю. Когда возникает перекос, растет уравнительный ток и напряжение смещения. Увеличение первого приводит к росту потерь, второго – к нестабильному функционированию бытовых приборов или другого оборудования, срабатыванию защитных устройств, быстрому износу электроизоляции и т.д.

Перечислим, какие последствия можно ожидать, когда появляется перекос:

Не следует забывать, что перекос может создать угрозу для жизни. При превышении номинального напряжения вероятность КЗ в проводке не велика, при условии, что она не ветхая, а кабель подобран правильно. Более опасны в этом случае электроприборы, подключенные к сети. Когда появляется перекос, может произойти КЗ на корпус или возгорания электроприбора.

Защита от перекоса фаз в трехфазной сети

Наиболее простой, но, тем не менее, эффективный способ минимизировать негативные последствия описанного выше отклонения — установить реле контроля фаз. С внешним видом такого устройства и примером его подключения (в данном случае после трехфазного счетчика), можно ознакомиться ниже.

Данный трехфазный автомат может обладать следующими функциями:

Совместно с реле контроля фаз можно использовать трехфазные стабилизаторы напряжения, с их помощью можно несколько улучшить качество электроэнергии. Но данный вариант не отличается эффективностью, поскольку такие приборы сами могут взывать нарушение симметрии, помимо этого на стабилизаторах возникают потери.

Лучший способ симметрировать фазы – использовать для этой цели специальный трансформатор. Этот вариант выравнивания фаз может дать результаты, как при неправильном распределении однофазных нагрузок на автономный 3-х фазный генератор электроэнергии, так и в более серьезных масштабах.

Защита в однофазной сети

В данном случае повлиять на внешние проявления системы электроснабжения не представляется возможным, например, если фазы перегружены, потребители электроэнергии не могут исправить ситуацию. Все, что можно сделать, это обезопасить электрооборудование путем установки реле напряжения и однофазного стабилизатора.

Имеет смысл установить общее стабилизирующее устройство на всю квартиру или дом. В этом случае необходимо высчитать максимальную нагрузку, после этого добавить запас 15-20%.. Это запас на будущее, поскольку со временем количество электрооборудования может увеличиться.

Совсем не обязательно подключать к стабилизатору сети все оборудование, некоторые виды приборов (например, электропечи или бойлеры), могут быть подключены к реле напряжения (через АВ) напрямую. Это позволит сэкономить, поскольку устройства меньшей мощности стоят дешевле.

Источник

Трехфазные несимметричные цепи

Содержание:

Трехфазные несимметричные цепи:

Трехфазная цепь несимметрична, если комплексы сопротивлений ее фаз неодинаковы.

Расчет несимметричной трехфазной цепи при соединении источника и приемника звездой

На схеме (см. рис. 20.4) видно, что при соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами — нейтральными точками N и N’. Наиболее удобным методом расчета в данном случае является метод узлового напряжения.

Определение токов

Рассмотрим сначала общий случай расчета цепи с нулевым проводом, сопротивление которого Z_N. При этом сделаем некоторые упрощения: сопротивления линейных проводов и фаз источников будем полагать равными нулю. Если указанные сопротивления нельзя считать равными нулю, их можно отнести к приемнику, прибавив к сопротивлениям последнего по правилам сложения комплексов.
При таком упрощении потенциалы линейных зажимов источника и приемника (например, точек А и А’) можно считать одинаковыми.
Напряжение между нулевыми точками N и N’, или узловое напряжение

Смещение нейтрали

На рис. 21.1 изображена топографическая диаграмма цепи рис. 20.4, а при несимметричной нагрузке.

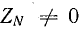
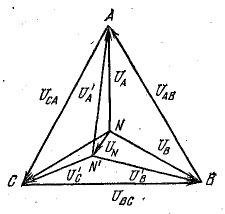
При наличии сопротивления в нулевом проводе () нулевая точка приемника на топографической диаграмме не совпадает с нулевой точкой источника. Поэтому напряжение U_N называют напряжением смещения нейтрали. Вследствие смещения нейтрали напряжения на фазах приемника оказываются неодинаковыми, несмотря на симметрию фазных напряжений источника (см. решение задачи 21.3).

Рис. 21.1. Топографическая диаграмма при несимметричной нагрузке (соединение звездой)

Из формулы (21.1) видно, что симметрия фазных напряжений на нагрузке, когда U_N = 0, достигается в двух частных случаях.
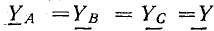
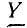
1. При симметричной нагрузке, когда комплексы проводимостей фаз равны: . В этом случае в числителе проводимость можно вынести за скобку, внутри которой складывается три вектора э. д. с. источника, равных по величине и сдвинутых по фазе на 120°; эта сумма равна нулю (см. рис. 20.8, б) и U_N = 0. Поэтому ток в нулевом проводе равен нулю [см. формулу (21.4)] и необходимость в этом проводе отпадает, а электроснабжение симметричных приемников осуществляется по трехпроводной системе.
2. В четырехпроводной системе, когда сопротивление нулевого провода равно нулю (Y_N = ∞.)

Роль нулевого провода

Нулевой провод является уравнительным. Потенциалы нейтрали источника и приемника с помощью этого провода принудительно уравнены, а поэтому звезда векторов фазных напряжений приемника точно совпадает со звездой фазных напряжений источника.

Четырехпроводная система применяется в электрических сетях с напряжением 380/220 В при электроснабжении от общего источника силовой (электродвигатели) и осветительной (электролампы) нагрузки.
При несимметричной нагрузке обрыв нулевого провода (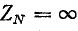) вызывает значительное изменение токов и фазных напряжений, что в большинстве случаев недопустимо. Поэтому в нулевой провод предохранители не устанавливаются.

Определение мощности

При несимметричной нагрузке нужно определить мощность каждой фазы. Например, для фазы А:

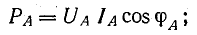
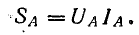
Аналогично определяются мощности других фаз.
Активная мощность всей трехфазной цепи равна сумме мощностей фаз:

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей фаз:

В этой сумме реактивная мощность катушки считается положительной, а реактивная мощность конденсатора — отрицательной.

Задача 21.1.

При соединении звездой с нулевым проводом определить фазные напряжения и токи в приемнике энергии, сопротивления которого заданы комплексами:

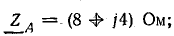
Действующая величина симметричной трехфазной системы э. д. с. 220 В. Сопротивление нулевого провода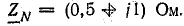
Построить векторную диаграмму.
Сопротивлениями линейных проводов и внутренними сопротивлениями источника э. д. с. пренебречь.
Решение. Схема, соответствующая условию задачи, показана на рис. 21.2, а.
Проводимости ветвей между узловыми точками NN’: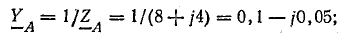

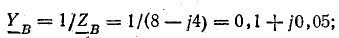
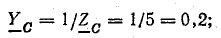
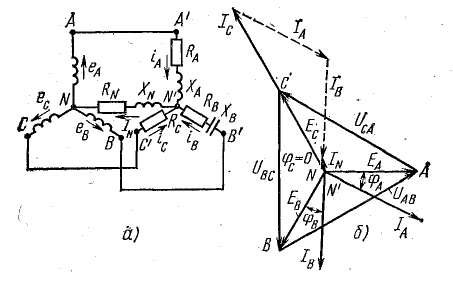
Рис. 21.2. К задаче 21.1

Комплексы э. д. с. источника:

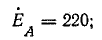
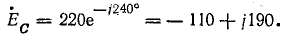
Узловое напряжение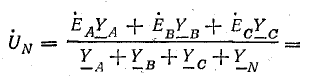



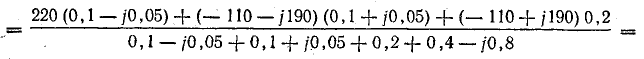
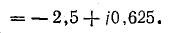
Фазные напряжения приемника: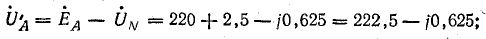



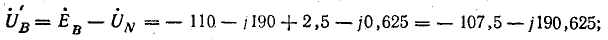
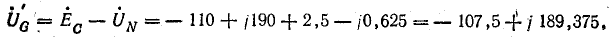
Токи в фазах и нулевом проводе: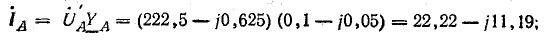




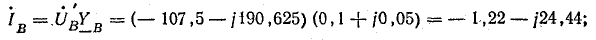
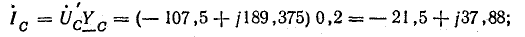
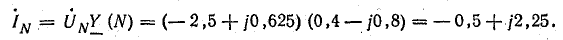
Векторная диаграмма напряжений и токов показана на рис. 21.2, б.

Задача 21.3.

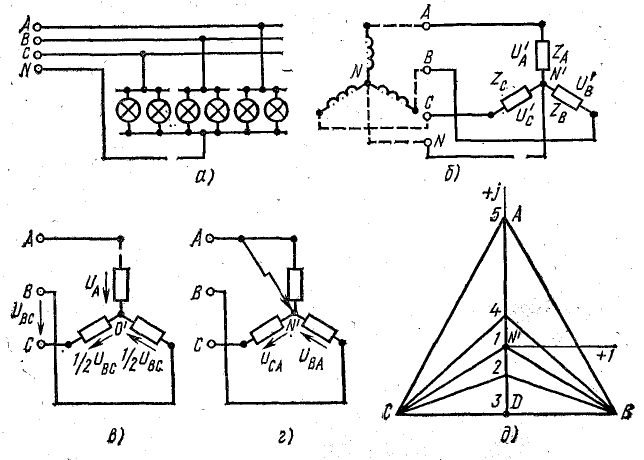
Электрические лампы включены звездой в трехфазную сеть с линейным напряжением 380 В. В каждую фазу включены по 50 ламп с номинальной мощностью 60 Вт каждая, номинальным напряжением 220 В. Как изменяются фазные напряжения и токи при изменении нагрузки одной фазы от холостого хода до короткого замыкания при обрыве нулевого провода?
В каждом выбранном случае нагрузки построить векторную диаграмму, определить мощность всей трехфазной цепи.
Решение. Условию задачи соответствует схема рис. 21.3, а, на которой группа ламп в каждой фазе условно показана двумя лампами.
Оставляя постоянным число ламп в фазах В и С, будем менять его в фазе А. Подсчеты по условию задачи выполним для таких нагрузок в фазе А: 50, 25, 100 ламп, короткое замыкание, холостой ход.
1. При включении в каждую фазу по 50 одинаковых ламп нагрузка симметрична. Поэтому фазные напряжения на нагрузке равны фазным напряжениям в сети: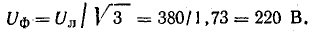

Напряжение на лампах равно номинальному. В этом случае лампы работают с номинальной мощностью.
Это даёт право определить фазные токи по заданной мощности ламп: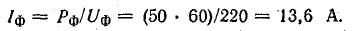

При соединении звездой I_Ф = I_Л, поэтому I_л = 13,6 А. Общая мощность трехфазной цепи
Р = ЗР_Ф = 3 • 60 • 50 = 9000 Вт.
2. В фазе А включено 25 ламп.
При несимметричной нагрузке напряжения на лампах отличаются от фазных напряжений в сети. Поэтому определить токи по заданной мощности ламп нельзя, так как действительная мощность ламп и фазные напряжения их неизвестны. При решении задачи будем считать, что сопротивление ламп в накаленном состоянии нити практически не меняется при некотором изменении их мощности.
Сопротивление лампы в номинальном режиме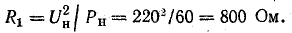

Сопротивление фаз В и С при включении 50 ламп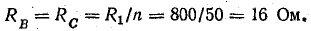

Сопротивление фазы А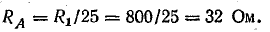

Комплексы фазных напряжений в сети:


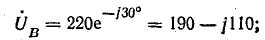
Проводимости ветвей:

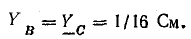
Смещение нейтрали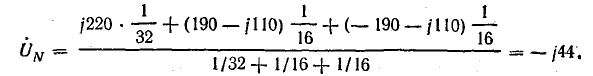

Напряжения фаз: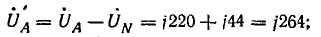



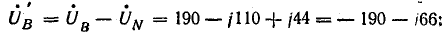
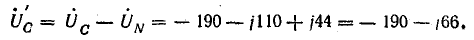
Токи в фазах: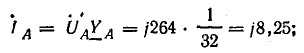



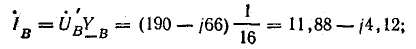
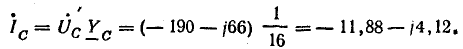
Мощность всех ламп в фазах: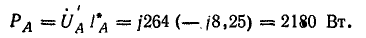



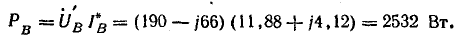
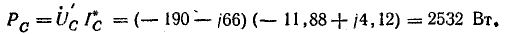
Мощность одной лампы: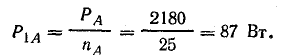



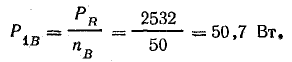
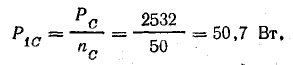
Общая мощность в трехфазной системе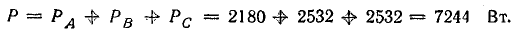

Векторная диаграмма напряжений для различной нагрузки фазы А показана на рис. 21.3, д.

Положение нулевой точки на диаграмме соответствует такой нагрузке фазы А: 1 — симметричная нагрузка (во всех фазах по 50 ламп); 2 — в фазе А 25 ламп; 3 — фаза А разомкнута (холостой ход); 4 — в фазе А 100 ламп; 5 — в фазе А короткое замыкание.

Выполните расчет трехфазной цепи для случаев нагрузки 3, 4, 5 подобно приведенному расчету для случая нагрузки 2, проверьте соответствие результатов расчета векторной диаграмме рис. 21.3, д.
Как видно, нулевая точка нагрузки при изменении проводимости фазы А перемещается на прямой АD, которая является перпендикуляром, опущенным из точки А к вектору линейного напряжения U_BC. При холостом ходе фазы А (обрыв линейного провода в этой фазе) нулевая точка перемещается в точку D и напряжения на двух других фазах U_B и U_C по величине оказываются равными половине линейного напряжения U_BC (рис. 21.3, б).

Рис. 21.3. К задаче 21.3

То же следует из схемы рис. 21.3, в. В рассматриваемом случае сопротивления фаз В и С оказываются включенными последовательно на линейное напряжение U_BC.

Сопротивления эти равны, поэтому линейное напряжение делится между двумя фазами поровну.

При коротком замыкании фазы А линейный провод этой фазы подводится непосредственно к нулевой точке нагрузки (рис. 21.3, г). Поэтому лампы, включенные в фазы В и С, оказываются под линейным напряжением.

Расчет несимметричной трехфазной цепи при соединении треугольником

Трехфазная цепь при соединении приемника треугольником и любой схеме соединения фаз источника имеет разветвленную многоконтурную схему (см., например, рис. 20.8, а; 21.5).

Расчет такой цепи выполняется одним из известных методов с учетом состава ее элементов и схемы соединения.

Соединение источника и приемника треугольником

Расчет сложной цепи (см. рис. 20.8, а) значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае напряжения на фазах приемника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.
Если трехфазная система напряжений, приложенных к приемнику, известна, то фазные токи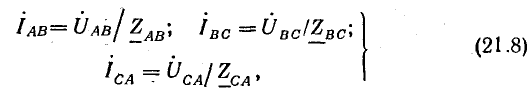
где 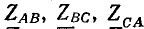— полные сопротивления фаз.
Линейные токи можно определить графически, как показано на рис. 21.4. Если задача решается в комплексной форме, линейные токи находят по формулам (20.7).

Мощность в несимметричной трехфазной цепи при соединении треугольником определяют по тем же формулам, что и при соединении звездой (21.6), (21.7).

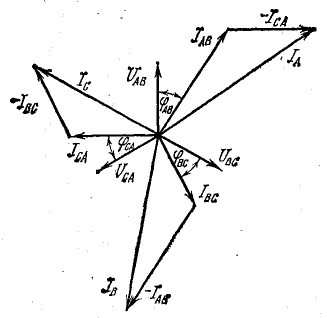
Рис. 21.4. Векторная диаграмма токов при несимметричной нагрузке (соединение треугольником)

Рис. 21.5. К вопросу о преобразовании треугольника сопротивлений в эквивалентную звезду в трехфазной цепи

Преобразование звезды и треугольника сопротивлений в трехфазных цепях

Расчет трехфазных цепей при смешанном соединении (звездой и треугольником), с учетом сопротивлений проводов линии представляет значительные трудности.

В этих случаях упрощения достигаются благодаря применению метода взаимного преобразования звезды и треугольника.
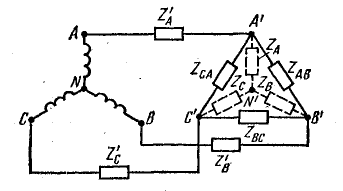
На рис. 21.5 приемник энергии соединен треугольником. С учетом сопротивлений проводов линии (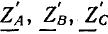) расчет такой цепи удобно выполнить, заменив треугольник сопротивлений эквивалентной звездой. Общее сопротивление фазы определяется сложением сопротивлений проводов линии и эквивалентной звезды приемника.

Если в ходе расчета схемы со смешанным соединением приемников — звездой и треугольником (рис. 21.6) — необходимо определить общее сопротивление фазы, это делается преобразованием звезды в треугольник или треугольника в звезду.
При симметричной нагрузке можно преобразовать треугольник в звезду, а затем две звезды заменить одной. Последняя операция возможна только при симметричной нагрузке, когда фазные напряжения у этих «звезд» одинаковы (смещение нейтрали отсутствует). При несимметричной нагрузке звезду следует преобразовать в эквивалентный треугольник, а затем сложением соответствующих проводимостей определить общую проводимость каждой фазы.

Рис. 21.6. к расчету трехфазной цепи при соединении приемников звездой и треугольником

Если в последнем случае требуется учесть сопротивление проводов, то общий треугольник еще раз приходится преобразовать в звезду и к сопротивлениям звезды прибавить сопротивления проводов линии.

Задача 21.4.

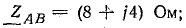
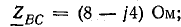
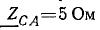
Сопротивления фаз приемника подключены треугольником к трехфазному генератору, обмотки которого также соединены треугольником. Действующие значения симметричной системы э. д. с. генератора 220 В. Пренебрегая сопротивлениями линейных проводов и обмоток генератора, определить фазные и линейные токи, активную, реактивную и полную мощности каждой фазы и всей цепи. Построить векторную диаграмму.
Решение. Схема рис. 20.8, а соответствует условию задачи. Если сопротивления линейных проводов и обмоток генератора считать равными нулю, то фазные напряжения приемника равны соответствующим э. д. с.:

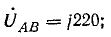
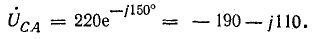
Фазные токи в приемнике: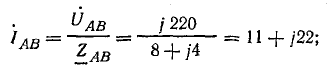



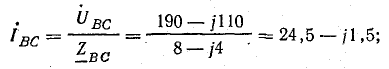
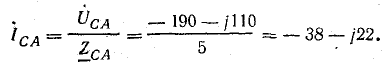
Линейные токи: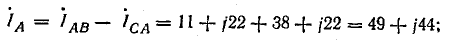



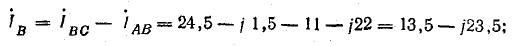
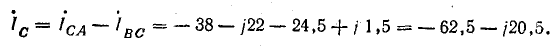
Сумма линейных токов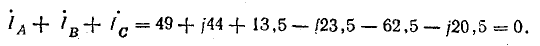

Равенство нулю суммы линейных токов является общим свойством трехфазных трехпроводных цепей при соединении звездой и треугольником при симметричной и несимметричной нагрузках.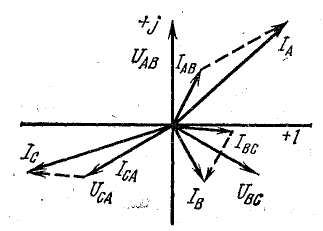

Рис. 21.7. К задаче 21.4

Рис. 21.8. К задаче 21.5

Мощности фаз: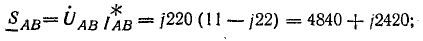



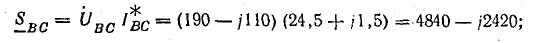
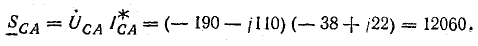
Общая мощность системы:
активная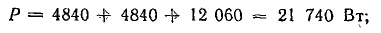

реактивная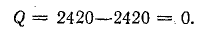

Векторная диаграмма построена на рис. 21.7.

Задача 21.5.

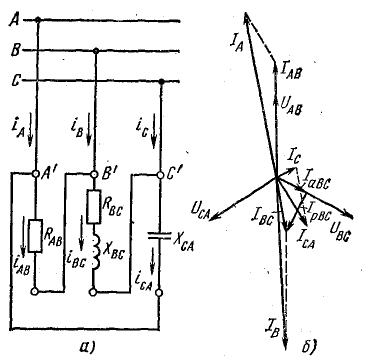
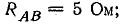
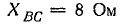
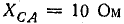
Приемник электрической энергии, соединенный треугольником, включен в сеть с линейным напряжением 120 В. Сопротивления фаз: (инд.); (емк.).
Начертить схему по условию задачи. Определить фазные и линейные токи, активную, реактивную и полную мощности в каждой фазе и всей цени. Построить векторную диаграмму.
Решение. Схема цепи изображена на рис. 21.8, а.
Решим задачу без применения комплексных чисел. Токи в фазах: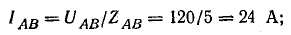



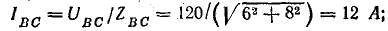
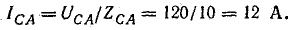
Линейные токи определим графически с помощью векторной диаграммы. Для этого найдем активные и реактивные токи фаз.
В фазе АВ включено активное сопротивление, поэтому

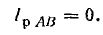
В фазе ВС последовательно соединены R и Х_L, поэтому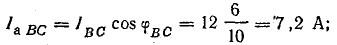


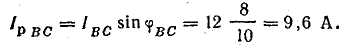
В фазе CA включено емкостное сопротивление, следовательно,

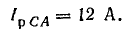
Векторная диаграмма цепи показана на рис. 21.8, б. Для определения линейных токов постройте векторную диаграмму на листе миллиметровой бумаги в масштабах: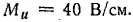
Линейные токи: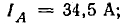
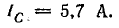
Мощности фаз:
активные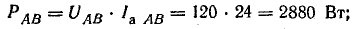

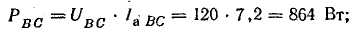
реактивные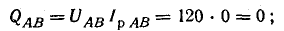



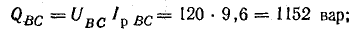
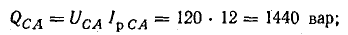
полные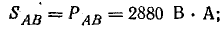



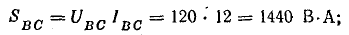
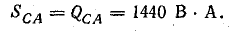
Мощность всей цепи:
активная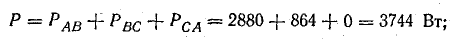

реактивная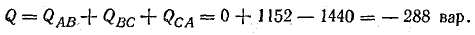

Знак минус указывает на емкостный характер реактивной мощности цепи.

Симметричные составляющие несимметричной трехфазной системы

Несимметричную трехфазную систему токов (напряжений или других синусоидальных величин) можно представить в виде суммы трех симметричных систем.

Разложение несимметричной системы векторов на симметричные составляющие применяется для расчета и анализа несимметричных режимов в трехфазных цепях: при симметричной нагрузке, но несимметричной системе э. д. с., при однофазных и двухфазных коротких замыканиях, при обрыве линейных проводов в цепях с симметричной системой э. д. с.

Комплексы симметричных составляющих

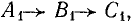
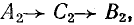
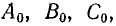
Первая симметричная система имеет прямую последовательность фаз ( рис. 21.9, а), вторая — обратную ( рис. 21.9, б). Третья система, называемая системой нулевой последовательности, состоит из трех равных величин, совпадающих по фазе ( рис. 21.9, в).

Рис. 21.9. Симметричные составляющие несимметричной системы

Разложение несимметричной системы на симметричные составляющие

Выразим комплексы несимметричной системы через симметричные составляющие: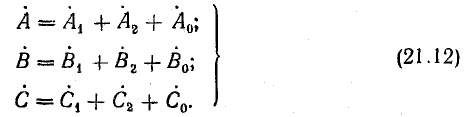

Если из этой системы уравнений можно однозначно определить симметричные составляющие через известные величины 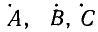несимметричной системы, то этим будет доказана возможность разложения несимметричной системы на три симметричные — прямой, обратной и нулевой последовательности.
Используя выражения (21.10), запишем систему уравнений (21.12) в таком виде: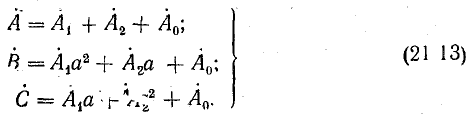

Решение системы уравнений (21.13) позволяет найти симметричные составляющие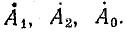
Сложим уравнения: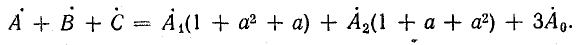

Учитывая формулу (21.11), найдем

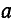
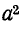
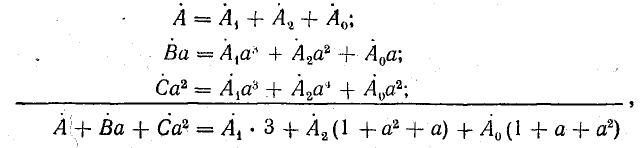
Умножим второе уравнение в системе (21.13) на , а третье — на и сложим все уравнения:

откуда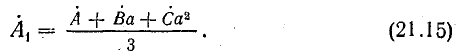

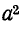
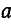
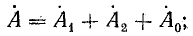
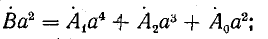
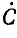
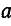
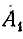
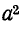
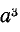
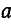
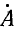
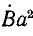
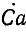
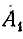
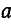
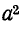
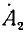
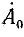
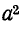
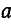
Умножим второе уравнение в системе (21.13) на , а третье на и сложим все уравнения:


= + ₊

+ + = (1 + + ) + • 3 + (1 + + )
откуда
= (21.16)

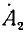
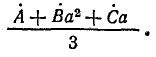
Свойства трехфазных цепей

Отметим некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений.

Степень несимметрии линейных напряжений оценивается коэффициентом несимметрии, т.е. отношением составляющей обратной последовательности напряжений к составляющей прямой последовательности.
ε = 100 • U_оп/U_пп.
Отсюда следует, что ток в нулевом проводе можно найти, если утроить величину составляющей тока нулевой последовательности.
В трехпроводной системе сумма линейных токов равна нулю. Из формулы (21.14) следует, что линейные токи в этом случае не содержат составляющей нулевой последовательности. Это справедливо и для линейных напряжений трехфазной системы, сумма которых тоже равна нулю.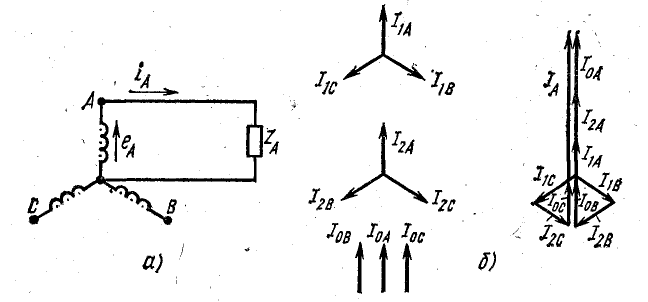

Рис. 21.10. Симметричные составляющие токов трехфазной цепи при разомкнутых двух фазах

Отсутствие тока в одной или двух фазах при несимметричном режиме означает, что сумма трех симметричных составляющих токов в этих фазах равна нулю.
Например, на схеме рис. 21.10, а фазы В и С разомкнуты. Поэтому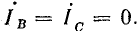
Согласно формулам (21.14) — (21.16), симметричные составляющие токов имеют следующие выражения:
прямой последовательности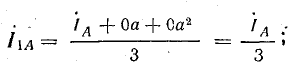

обратной последовательности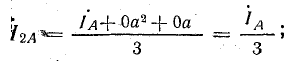

нулевой последовательности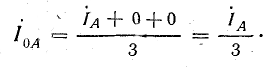

На рис. 21.10, б показаны симметричные составляющие прямой, обратной и нулевой последовательности и их геометрическое сложение; в результате сложения получаем: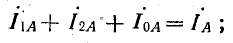

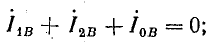
Задача 21.8.

В результате неправильной маркировки концов обмоток трехфазного трансформатора (начало фазы А вторичной обмотки помечено как конец) система линейных напряжений несимметрична. Определить симметричные составляющие линейных напряжений при соединении звездой, если фазные напряжения во вторичной обмотке 220 В.
Решение. Запишем комплексы фазных напряжений во вторичной обмотке: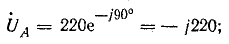



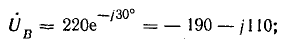
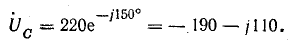
Вектор напряжения 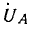в соответствии с условием задачи повернут на 180°.
Комплексы линейных напряжений: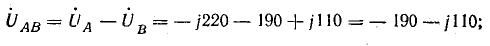



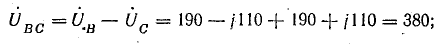
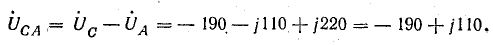
Составляющие:
нулевой последовательности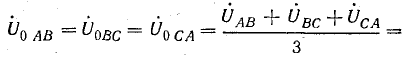


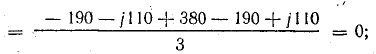
прямой последовательности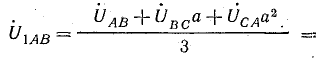




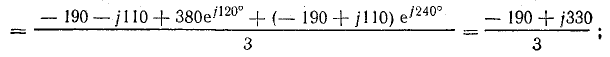
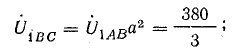
обратной последовательности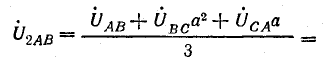

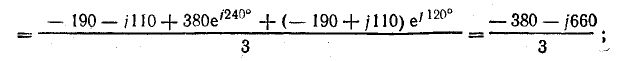
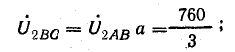
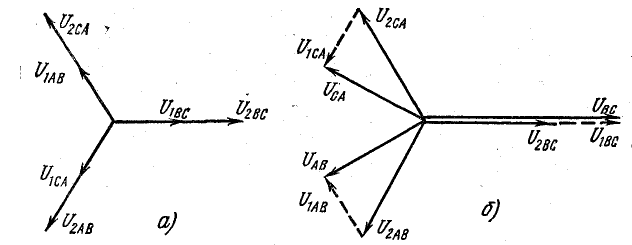
Рис. 21.11. К задаче 21.8

На рис. 21.11, а, б показаны векторы систем прямой и обратной последовательности и их сумма — система трех исходных векторов линейных напряжений.

Задача 21.9.

Трехфазный электродвигатель, включенный в сеть с линейным напряжением 380 В при соединении звездой, имеет мощность на валу Р₂ = 14 кВт; соsφ = 0,8; к. п. д. η = 0,85.
Определить симметричные составляющие токов в обмотке двигателя при обрыве линейного провода в фазе В.
Решение. При нормальной работе ток в фазе двигателя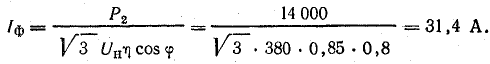

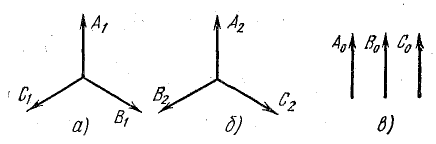
При симметричной системе напряжений токи в фазах двигателя образуют симметричную систему (рис. 21.12, а). При обрыве линейного провода В векторная диаграмма фазных напряжений и токов показана на рис. 21.12, б.
Ток в фазах В равен нулю (I_B = 0).
Токи в фазах А и С равны по величине, но находятся в противофазе: I_А = I_C.
Для определения величины токов I_А и I_C найдем расчетное сопротивление фазы двигателя при нормальном режиме, которое будем считать неизменным: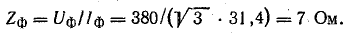

При обрыве линейного провода фазы В обмотки двух других фаз двигателя с одинаковым сопротивлением включены последовательно на линейное напряжение U_CA. Поэтому ток в фазах А и С

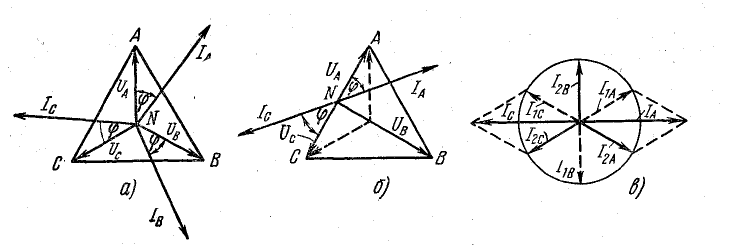
Рис. 21.12. к задаче 21.9

Выразим токи в комплексной форме, полагая ток I_A совпадающим с положительным направлением действительной оси:

Токи:
нулевой последовательности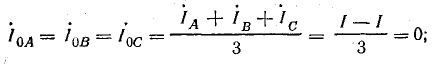

прямой последовательности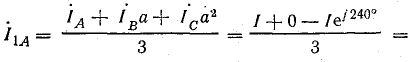



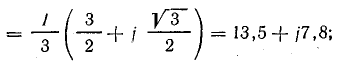
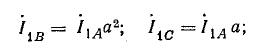
обратной последовательности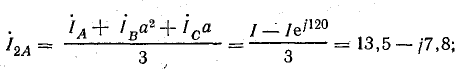

На рис. 21.12, в изображены симметричные составляющие токов в двигателе при обрыве фазы.

Несимметричный режим работы трехфазной цепи

Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством э. д. с. и т. п.

Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же

методами, которые применяются для расчета однофазных цепей.

Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).

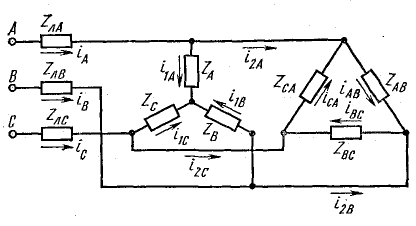
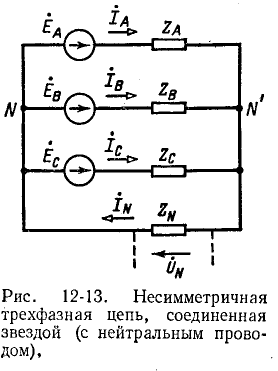
1. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 12-13).

Несимметричная трехфазная цепь, показанная на рис. 12-13, может рассматриваться как трехконтурная цепь с тремя э. д. с. Такая цепь может быть рассчитана методами контурных токов, узловых напряжений и другими. Поскольку в схеме имеются только два узла, наиболее целесообразно в данном случае определить узловое напряжение (напряжение смещения) между нейтральными точками N’ и N по формуле,

где 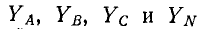— проводимости соответствующих ветвей.

После этого найдем токи:

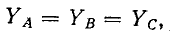
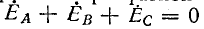
В симметричной трехфазной цепи и поэтому при узловое напряжение равно нулю.

Стучаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода. j

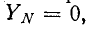
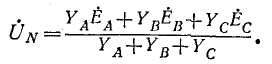
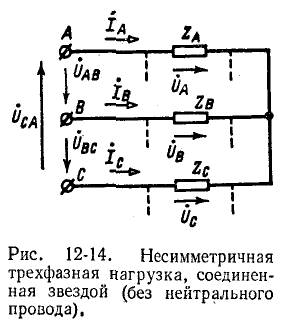
При отсутствии нейтрального провода, полагая в (12-1), имеем:

2. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями на выводах (рис. 12-14).

Если заданы линейные напряжения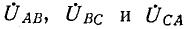на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.

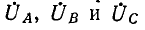
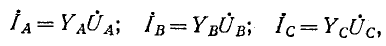
Обозначив фазные напряжения на выводах нагрузки через(рис. 12-14), получим

где 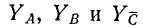— проводимости фаз нагрузки.

Равенство нулю суммы токов трех фаз записывается в виде:

Фазные напряжения могут быть выражены через и заданные линейные напряжения: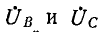

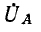
Подстановка (12-3) в (12-2) дает:

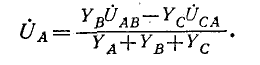
Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся: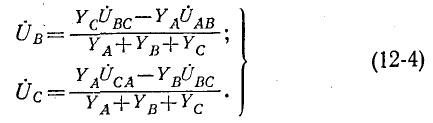

По фазным напряжениям нагрузки находятся фазные токи.

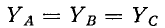
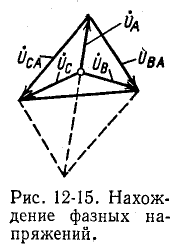
В Случае симметричной нагрузки вектор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих линейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника.

На рис. 12-15 построение сделано для фазы А по формуле (12-4)1

В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой.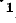

Положим, что конденсатор присоединен к фазе А, лампы — к фазам В и С; емкостное сопротивление конденсатора берется равным по модулю сопротивлению лампы, т. е. 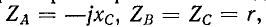причем

Неравенство напряжений на лампах проявится в том, что накал ламп будет разным.

1 Для определения чередования фаз на практике обычно пользуются специальным прибором, в котором создается вращающееся магнитное поле, увлекающее за собой диск в ту или другую сторону.

Отношение напряжений согласно выведенным выше выражениям (12-4) равно при симметрии линейных напряжений:

Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоединенная к отстающей фазе, — тускло.

Вместо конденсатора можно применить индуктивную катушку, подобрав ее индуктивное сопротивление приблизительно равным по модулю сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе. Эти соотношения также могут быть получены непосредственно из векторной диаграммы.

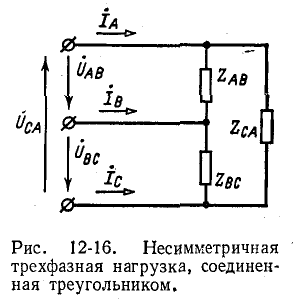
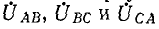
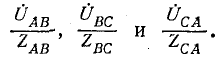
3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на выводах Рис. 12-16. Несимметричная (рис. 12-16). Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения (рис. 12-16), то токи в сопротивлениях нагрузки равны:

Токи в линии определяются как разности соответствующих токов нагрузки, например: 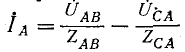и т. д.

Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения 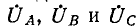источника, соединенного в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмотренному случаю(рис. 12-16).
Пример 12-2. Сопротивления фаз нагрузки, соединенной звездной

Сопротивление нейтрального провода

Напряжения на цепи представляют собой симметричную звезду:

Требуется определить фазные напряжения нагрузки.

Проводимости фаз нагрузки и нейтрального провода

На основании формулы (12-1)

Искомые фазные напряжения нагрузки:

Мощность несимметричной трехфазной цепи

Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:

Действительная часть этого выражения представляет собой активную мощность

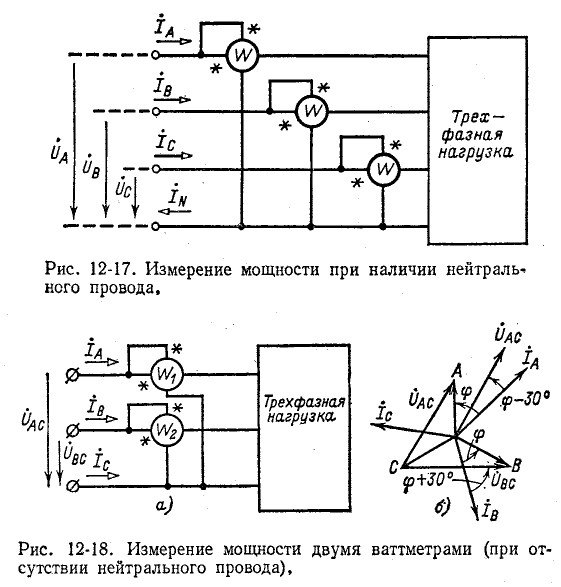
Суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть в соответствии с этим измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения относительно нейтрали и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода (рис. 12-17) или искусственно созданной нейтральной точки.

В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ваттметров

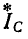
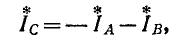
(рис. 12-18). В этом случае выражение (12-5) преобразуется следующим образом: исключая ток с помощью условия
получаем:

или

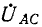
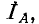
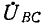
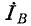
В соответствии с (12-6) при измерении активной мощности двумя ваттметрами к одному из них подводятся напряжение и ток а ко второму — напряжение и ток (рис. 12-18, а). Показания ваттметров складываются алгебраически.

Круговой заменой А, В. и С в выражении (12-6) можно получить выражения для других равноценных вариантов включения двух ваттметров.

Следует иметь в виду’, что если стрелка одного ваттметра отклоняется по шкале в обратную сторону, то, изменив направление напряжения или тока, подводимого к данному ваттметру, записывают полученное показание со знаком минус. При симметричном режиме работы трехфазной цепи такое положение имеет место при

что видно непосредственно из векторной диаграммы (рис. 12-18, б).

При симметричном режиме показания двух ваттметров в схеме рис. 12-18, б будут следующие:

Сумма и разность показаний ваттметров соответственно равны:

Следовательно, при симметричном режиме работы трехфазной цепи тангенс угла сдвига фаз может быть вычислен по формуле

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник