деление по модулю что это
Введение в модулярную арифметику
Для любой системы взаимно простых чисел p1, … pn, любое число X из диапазона [0; M), где M = p1*p2*…*pn взаимооднозначно представимо в виде вектора (a1, a2, …, an), где ai = X%pi (здесь и далее «%» — операция взятия остатка от целочисленного деления X на pi).
p1, … pn – модули системы
a1, a2, …, an – остатки (вычеты) числа по заданной системе модулей
Прямое преобразование
Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.
Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).
Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p
Любое число X можно записать в виде X%p = (xn-1*2 n-1 + xn-2*2 n-2 + x0*2 0 )%p = ((xn-1)%p*2 n-1 %p) + ((xn-2)%p*2 n-2 %p) + … + x0%p)%p. Поскольку в данном случае xn-1, … x0 равны 0 или 1, то фактически нам требуется сложить вычеты вида (2 i %p).
Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*2 4 + 1*2 3 + 0*2 2 + 0* 1 + 1*2 0 )%7 = (2 4 %7 + 2 3 %7 + 1%7)%7 = (2 + 1 + 1)%7 = 4
Арифметические операции
Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)
Обратное преобразование
Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x1, x2, … xn) = (x1, 0, …, 0) + (0, x2, …, 0) + … + (0, 0, …., xn) = x1*(1, 0, …, 0) + x2*(0, 1, …, 0) + … + xn*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (Mi*bi)%pi = 1, где Mi = M/pi, а bi – искомое число. В этом случае позиционное представление Bi = Mi*bi и
X = (x1*(M1*b1) + x2*(M2*b2) + … + xn*(Mn*bn))%M
Пример: пусть задана система модулей (3, 5, 7), найдем значения Mi и bi (0 b1 = 2
(21*b2)%5 = 1 => b2 = 1
(15*b3)%7 = 1 => b3 = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8
Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M1, …, Mn), а так же операция взятия остатка по модулю большого числа M.
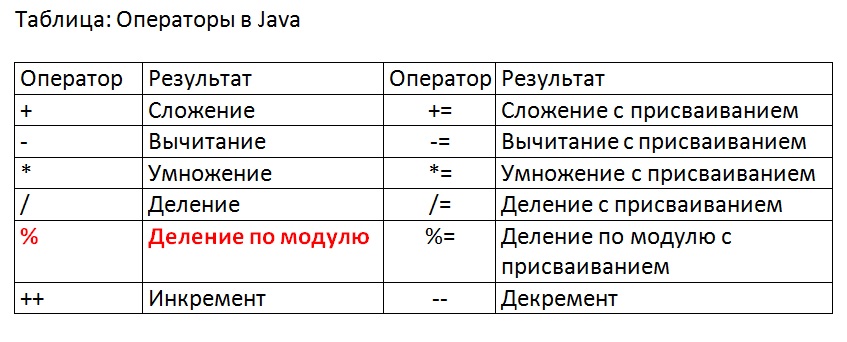
Деление по модулю в Java
Ещё со школы мы знакомы с таким понятием как обычное деление:
Как работает оператор сложения, вычитания и т.д. наверняка Вы уже знаете. А вот за что отвечает деление по модулю поймёте буквально через пару минут. Немного терпения.
Давайте посмотрим на примерах как это работает.
Пример №1
Необходимо разделить 9 на 4, используя:
Логику работы оператора деления по модулю Вы уже поняли. Самое время попробовать запустить пример на своём компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
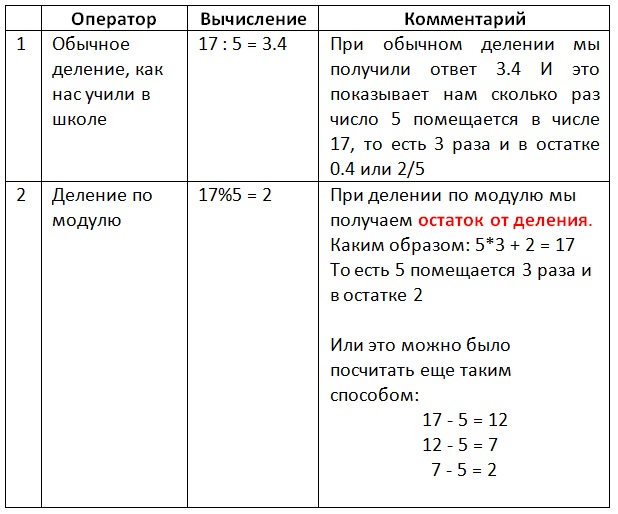
Пример №2
Необходимо разделить 17 на 5, используя:
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
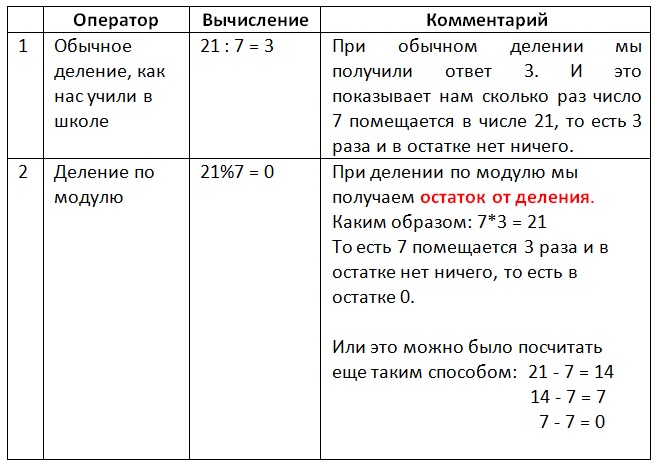
Пример №3
Необходимо разделить 21 на 7, используя:
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено такое число:
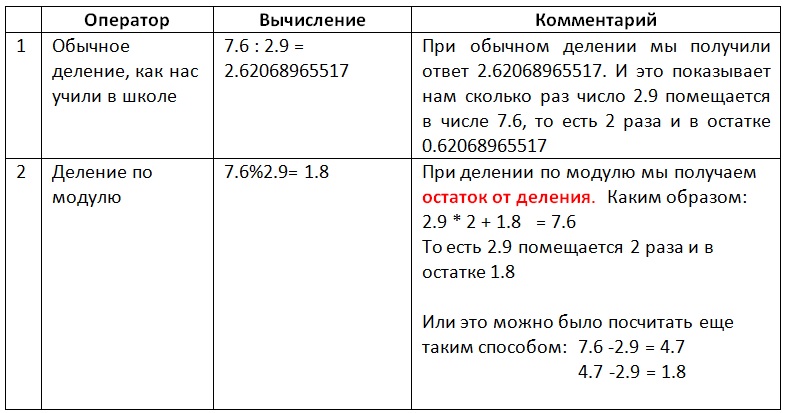
Пример №4
Необходимо разделить 7.6 на 2.9, используя:
И пробуем теперь запустить программу на компьютере:
Если Вы запустите этот код на своём компьютере, то в консоль будет выведено число, близкое к 1.8. Например, Вы можете увидеть какое-то такое число: 1.7999999999999998. Из-за определённых особенностей Java, которые мы будем с Вами рассматривать позже в других статьях, на разных компьютерах число будет немного отличаться. Но оно будет близкое по значению к 1.8
Итак, как Вы уже поняли, оператор деления по модулю вычисляет остаток от деления.
Есть небольшой нюанс при использовании оператора деления по модулю с отрицательными и положительными числами.
Работает простое правило:
Пример №5
«Деление» по модулю
Обычные арифметические операции по модулю выполняются не сильно сложнее — просто нужно брать модули и заботиться о переполнении. Например:
Но вот с делением возникают проблемы — мы не можем просто взять и поделить.
Через бинарное возведение в степень
Этот подход простой и быстрый, однако следует помнить, что он работает только для простых модулей.
Через расширенный алгоритм Евклида
Расширенный алгоритм Евклида можно использовать для решения в целых числах уравнений вида
Преимущества этого метода над возведением в степень:
Но лично автор почти всегда использует возведение в степень.
Упрощенная реализация
Сначала приведем реализацию, а потом поймем, почему она работает:
Докажем по индукции, что функция действительно возвращает обратный элемент.
Во втором случае проверим правильность формулы:
Предподсчет обратных элементов
Чаще всего нам нужно искать обратный элемент в контексте комбинаторики.
Например, особенно часто нужно считать биномиальные коэффициенты, для чего в свою очередь нужно уметь обращать факториалы:
Простой способ — это предпосчитать обычные факториалы и каждый раз вызывать inv один или два раза:
Однако это добавит лишний логарифм в асимптотику в нередком случае, когда какая-то комбинаторная формула лежит внутри горячего цикла. Поэтому имеет смысл предподсчитать и частые обратные элементы.
Обратные факториалы
Все остальные обратные факториалы можно таким же образом итеративно подсчитать из предыдущего.
Деление чисел с остатком
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Тогда необходимо взять q такое, чтобы данное неравенством b * q
Деление по модулю
Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).
Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.
Содержание
Определение
Для отрицательного делителя нужно округлять частное в большую сторону:
Операция «mod» и связь со сравнениями
b.>
В программировании
| Язык | Неполное частное | Остаток | Знак остатка |
|---|---|---|---|
| ActionScript | % | Делимое | |
| Ada | mod | Делитель | |
| rem | Делимое | ||
| Бейсик | \ | MOD | Не определено |
| Си (ISO 1990) | / | % | Не определено |
| Си (ISO 1999) | / | % | Делимое [3] |
| C++ (ISO 2003) | / | % | Не определено [4] |
| C++ (ISO 2011) | / | % | Делимое [5] |
| C# | / | % | Делимое |
| ColdFusion | MOD | Делимое | |
| Common Lisp | mod | Делитель | |
| rem | Делимое | ||
| D | / | % | Делимое [6] |
| Delphi | div | mod | Делимое |
| Eiffel | // | \\ | Делимое |
| Erlang | div | rem | Делимое |
| Euphoria | remainder | Делимое | |
| Microsoft Excel (англ.) | QUOTIENT() | MOD() | Делитель |
| Microsoft Excel (рус.) | ЧАСТНОЕ() | ОСТАТ() | |
| FileMaker | Div() | Mod() | Делитель |
| Fortran | mod | Делимое | |
| modulo | Делитель | ||
| GML (Game Maker) | div | mod | Делимое |
| Go | / | % | Делимое |
| Haskell | div | mod | Делитель |
| quot | rem | Делимое | |
| J | | |
Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.
Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа. Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается:
Знак остатка
Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:
Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.
Как запрограммировать, если такой операции нет?
Обобщения
Вещественные числа
Деление 7,9 на 2,1 с остатком даёт: