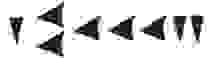действующие стандарты системы счислений шифров и кодов что это
ГОСТ 28147-89 (Часть 1. Введение и общие принципы)
Очень часто на Хабре встречаются статьи о сути, программных реализациях, вскрытиях шифров. Но непонятно одно: почему среди них нет наших, отечественных алгоритмов шифрования?
Я решил исправить это, написав повесть статью, разбитую на 5 частей для лучшего восприятия о стандарте ГОСТ 28147-89. Каждая часть, кроме первой (описывает схему алгоритма и общие принципы), повествует о каждом из четырех возможных режимах работы стандарта с приложением к ним кода на C++.
Описание алгоритма
ГОСТ 28147-89 является отечественным блочным шифром. То есть открытый текст разбивается на блоки (в данном случае 64 бита), и каждый блок преобразовывается отдельно.
В основу алгоритма положена сеть Фейстеля, представленная на рисунке ниже.
Поясню работу данной схемы.
Структурная схема алгоритма
Данная схема содержит:
Ключи
В КЗУ
КЗУ отведено 256 бит, в ГОСТ 28147-89 используется ключ длиной 256 бит. Ключ разбивается на восемь блоков по 32 бита, и каждый бит каждого блока последовательно вводится в накопитель X соответствующего порядка.
То есть, 1-й бит ключа вводится в 1-й разряд накопителя X0, 2-й — во 2-й разряд накопителя X0, 33-й — в 1-й разряд накопителя X1, 65-й — в 1-й разряд накопителя X2, и так далее, 224-й бит ключа вводится в 1-й разряд накопителя X7, 256-й бит ключа вводится в 32-й разряд накопителя X7.
Считывается же ключ в соответствии с выбранным режимом работы алгоритма, но в следующих частях статьи.
В блоке подстановки K
Блок подстановки содержит в себе таблицу замены размерностью 16×8, которая является долговременным ключом.
Строки таблицы определяют, грубо говоря, что требуется заменить (число от 0 до 15 в шестнадцатиричной системе счисления). Столбцы же указывают, на что заменять. При этом поступающий 32-битовый в блок вектор разбивается на восемь 4-х битовых, каждый из которых и преобразуется в соответствии с таблицой замены.
Ключи как в КЗУ, так и в блоке К, являются секретными, и требуются меры по недопущению их компрометации.
Режимы работы
UPD: Следующая часть статьи «Режим простой замены» доступен по ссылке.
Какие у администратора БД обязанности и KPI (показатели работы)?
2. На должность администратора баз данных назначается лицо, имеющее высшее математическое, экономическое или техническое образование и практику работы на персональных компьютерах не менее 3-х лет.
4. Администратор баз данных должен знать:
4.5. Методы классификации и кодирования информации.
4.6. Нормализованные языки программирования.
4.7. Действующие стандарты, системы счислений, шифров и кодов.
4.9. Порядок оформления технической документации.
4.10. Передовой отечественный и зарубежный опыт программирования и использования вычислительной техники.
4.11. Основы экономики, организации труда и управления.
Должностные обязанности:
Работа с накладными.
Ведение базы данных.
Товародвижение.
2.1. Анализирует информационные потребности структурных
подразделений предприятия.
2.7. Осуществляет систематическое обучение работников предприятия
приемам и навыкам работы на компьютерах, а также работе с внедряемыми
программными средствами.
2.8. Осуществляет контроль за работой компьютеров и своевременно
сообщает о сбоях и неисправностях в отдел информатизации.
2.9. Осуществляет учет и хранение документов, имеющих отношение к
автоматизированной обработке информации на компьютерах.
2.11. Следит за обеспечением целостности, достоверности и
сохранности циркулирующих в автоматизированной информационной системе
данных.
2.12. Ведет архив используемых программных средств и
нормативно-справочной информации.
2.13. Выдает руководству предприятия рекомендации по распределению
между структурными подразделениями поступающей вычислительной техники с
учетом наличия программного обеспечения, подготовленных специалистов и
анализа загрузки находящихся в эксплуатации ПЭВМ.
Основы систем счисления
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32: 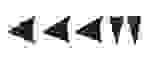
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92: 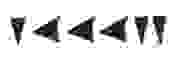
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа: 
Теперь число 3632 следует записывать, как:
Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10 2 + 0*10 1 + 3*10 0 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Q n (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Пример: 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ), (0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012
Исследовательская работа «КОДЫ И ШИФРЫ»
Муниципальное бюджетное общеобразовательное учреждение «СОШ с. Яковлевка Базарно-Карабулакского муниципального района Саратовской области»
обучающийся 10 класса
Дамаев Ряшит Харисович
Понятия «код» и «кодирование». Азбука Морзе.
Двоичное кодирование в компьютере.
Алгоритмы сжатия двоичного кода.
Понятия «шифр» и «шифрование».
Криптография в интересах государства.
Современные стандарты шифрования.
Терминология: в чём отличие и в чём сходство понятий «шифрование» и «кодирование». Оба понятия отображают процесс преобразования информации. При кодировании производится преобразование информации из одной формы в другую с абсолютно прозрачным алгоритмом преобразования, который позволяет однозначно определить содержание информации без искажений. А при шифровании форма представления информации может остаться прежней, а вот содержание восстановить трудно или вообще невозможно без знания алгоритмов шифрования и ключа шифра.
Можно сказать, что кодирование и шифрование – это процессы обработки информации, но имеющие разные цели. Кодирование производится с целью более удобной передачи, обработки или хранения информации, а шифрование – с целью защиты информации.
Понятия «код» и «кодирование». Азбука Морзе.
Код — правило (алгоритм) сопоставления каждому конкретному сообщению строго определённой комбинации символов (знаков) (или сигналов).
В повседневной жизни мы часто встречаемся с кодированной информацией: текст, запись чисел, нотная запись, формулы…
Очень интересным способом кодирования, который был технически реализован для передачи информации на большие расстояния с помощью световых, электрических и электромагнитных сигналов, является код Морзе (или «азбука Морзе») — способ знакового кодирования, представление букв алфавита, цифр, знаков препинания и других символов последовательностью сигналов: длинных («тире») и коротких («точек»). За единицу времени принимается длительность одной точки. Длительность тире равна трём точкам. Пауза между элементами одного знака — одна точка, между знаками в слове — 3 точки, между словами — 7 точек. Назван в честь американского изобретателя и художника Сэмюеля Морзе. Буквенные коды (собственно «азбука») были добавлены коллегой Морзе, Альфредом Вейлем — факт, который Морзе впоследствии всячески отрицал (а заодно приписывал себе изобретение телеграфа как такового). Вейлем же, возможно, была придумана и цифровая часть кода. А в 1848 году код Вейля/Морзе был усовершенствован немцем Фридрихом Герке. Код, усовершенствованный Герке, используется до настоящего времени. Современная телеграфная азбука (система кодировки символов короткими и длинными посылками для передачи их по линиям связи, известная как «код Морзе» или «морзянка») существенно отличается от той, что предложил в 1838 г. С. Морзе. Исходная таблица «кода Морзе» разительно отличалась от тех кодов, что сегодня звучат на любительских диапазонах. Во-первых, в ней использовались посылки трёх разных длительностей («точка», «тире» и «длинное тире» — в 4 раза длиннее «точки»). Во-вторых, некоторые символы имели паузы внутри своих кодов.
Принцип кодирования азбуки Морзе исходит из того, что буквы, которые чаще употребляются в английском языке, кодируются более простыми сочетаниями точек и тире. Это делает освоение азбуки Морзе проще, а передачи — компактнее.
Передаваться и приниматься азбука Морзе может с различной скоростью — это зависит от возможностей и опыта радистов. Обычно средней квалификации радист работает в диапазоне скоростей 60 — 100 знаков в минуту. Достижения по скоростным приёму-передаче находятся в диапазоне скоростей 260—310 знаков в минуту.
Одним из самых удобных принципов кодирования является двоичное кодирование, применяемое для представления и дальнейшей обработки информации в компьютере. Двоичный код — это способ представления данных в одном разряде в виде комбинации двух знаков, обычно обозначаемых цифрами 0 и 1 (двоичный алфавит). Разряд в этом случае называется двоичным разрядом. В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1». Двоичный код может быть непозиционным и позиционным. Позиционный двоичный код лежит в основе двоичной системы счисления, широко распространенной в современной цифровой технике.
Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.
Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. В школьном курсе информатики рассматривается двоичное кодирование в восьмеричной и шестнадцатеричной системах счисления где соответствие цифры и двоичного кода однозначно определяется связью N=2 k :
В двоично -десятичном кодировании также используется двоичный код для кодирования чисел в десятичной системе счисления.
При помощи четырех бит можно закодировать шестнадцать цифр. Из них используются 10. Остальные 6 комбинаций в двоично-десятичном коде являются запрещенными.
Таблица соответствия двоично-десятичного кода и десятичных цифр:
Двоично-десятичный код также применяется в телефонной связи. В этом случае кроме десятичных цифр кодируются символы ‘*’ или ‘#’ или любые другие. Для записи этих символов в двоично-десятичном коде используются «запрещенные» комбинации:
Часы с двоично-десятичной системой индикации. В этих часах каждая колонка отображает десятичное число в двоично-десятичной системе.
Упрощён вывод чисел на индикацию — вместо последовательного деления на 10 требуется просто вывести на индикацию каждый полубайт. Аналогично, проще ввод данных с цифровой клавиатуры.
Для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность.
Упрощены умножение и деление на 10, а также округление.
По этим причинам двоично-десятичный формат применяется в калькуляторах — калькулятор в простейших арифметических операциях должен выводить в точности такой же результат, какой подсчитает человек на бумаге.
Требует больше памяти.
Усложнены арифметические операции. Так как используются только 10 возможных комбинаций 4-х битового поля вместо 16, существуют запрещённые комбинации битов: 1010(10 10 ), 1011(11 10 ), 1100(12 10 ), 1101(13 10 ), 1110(14 10 ) и 1111(15 10 ).
При кодировании алфавитно-цифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.
При изучении информатики в школе на базовом уровне рассматривается только основные принципы применения двоичного кодирования для представления информации: числовой, текстовой, графической и звуковой (первичный код).
Примеры представления информации двоичными кодами.
Существуют алгоритмы дополнительного преобразования первичного двоичного кода, например, алгоритмы сжатия. Алгоритм Шеннона — Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Роберт Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона — Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов. Алгоритм Шеннона — Фано использует избыточность сообщения, заключённую в неоднородном распределении частот символов его (первичного) алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов — более длинными двоичными последовательностями. Алгоритм был независимо друг от друга разработан Шенноном (публикация «Математическая теория связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).
Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0. При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Пример кодового дерева
A (частота встречаемости 50)
B (частота встречаемости 39)
C (частота встречаемости 18)
D (частота встречаемости 49)
E (частота встречаемости 35)
F (частота встречаемости 24)
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона — Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона — Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Существует много методов (алгоритмов) преобразования первичных кодов с целью уменьшения общего информационного объёма данных с возможностью последующего восстановления исходных данных (полного или с потерями). Применимость каждого метода может быть универсальной или привязанной к конкретному виду информации. Например, метод сжатия с потерями может быть применён для аудио или графической информации, но не может быть применён к текстовой информации.
Шифрование – защита информации путём её преобразования с использованием определённых закрытых (в смысле доступности для всех) алгоритмов и ключей.
Наука о создании и использовании шифров называется криптографией.
Под шифром понимается совокупность методов и способов обратимого преобразования информации с целью ее защиты от несанкционированного доступа (обеспечения конфиденциальности информации).
Составными элементами шифра являются:
— алфавиты для записи исходных сообщений (защищаемой информации, открытого текста) и шифрованных сообщений (шифртекстов, шифрограмм, криптограмм);
— алгоритмы криптографического преобразования (шифрования и дешифрования);
— множество ключей (важным параметром любого шифра является ключ — параметр криптографического алгоритма, обеспечивающий выбор одного преобразования из совокупности преобразований, возможных для этого алгоритма.)
Шифрование информации применялось с древнейших времён.
Например, в древней Спарте было изобретено специальное устройство для шифрования текстов – сцитала. Сцитала представляла собой стержень, на который плотно, виток к витку наматывали ленту, затем на ней писали текст, располагая его вдоль оси стержня. Когда ленту снимали с цилиндра, на ней оставалась цепочка букв, на первый взгляд, совершенно беспорядочная. У получателя шифровки был такой же цилиндр, на который он наматывал полученную ленту, после этого текст опять становился понятным.
Другой известный с античности шифр называется по имени древнеримского императора Гая Юлия Цезаря. Суть этого кода состояла в том, что буква алфавита заменялась другой с помощью сдвига по алфавиту на одно и то же число позиций. Шифр Цезаря относится к простейшим методам шифрования – шифрам замены. Такие шифры легко поддаются расшифровке.
В Древней Греции (II в. до н. э.) был известен шифр, называемый «квадрат Полибия». Это устройство представляло собой квадрат 5х5, столбцы и строки которого нумеровались от 1 до 5. В каждую клетка этого квадрата записывалась одна буква (в греческом алфавит одна клетка оставалась пустой, а в латинском в одну клетку записывалось две буквы: I, J).
В результате каждой букве отвечала пара чисел, и шифрованное сообщение превращалось в последовательность пар чисел.
Шифр Гронфельда — шифр замены, использующий число в качестве ключа для текста. Под буквами письма, излагаемого шифром, подписываются по порядку цифры секретного числа одна за другою так, чтобы под каждой буквой стояла цифра; затем в письме вместо обыкновенных букв ставят другие буквы, отстоящие в общепринятой азбуке от первых на столько букв, сколько единиц в числе, обозначенном соответствующей цифрой.
В 1550 году, Джероламо Кардано, учёный энциклопедист эпохи Возрождения, предложил простую решётку для шифрования сообщений. Он планировал маскировать сообщения под обычное послание, так что в целом они не были полностью похожи на шифрованные.
Существует три вариации метода шифрования с помощью решетки Кардано. Изначально Кардано планировал маскировать сообщения под невинные послания, создавая стенограмму. Первоначально это был прямоугольный или квадратный трафарет (четких правил для его изготовления нет), изготовленный из листа картона или пергамента или же из тонкой металлической пластины, в котором в произвольном порядке вырезались прямоугольные отверстия, в которые помещались отдельные буквы, слоги или даже целые слова. Таких шаблонов изготавливалось как минимум два (по числу переписчиков). Перед тем как писать, бумагу разлиновывают, чтобы обозначить линии письма. Затем накладывают решетку Кардано. Последовательно в пустые клеточки вписывают текст послания, которое необходимо скрыть. Потом решетку убирают, а оставшееся пространство «дополняют» до какого-нибудь невинного послания. Стоит отметить, что сделать это так, чтобы послание не выделялось неестественностью языка, достаточно сложно и требует незаурядных литературных способностей и навыков. Но существенный плюс такого способа шифрования состоит в том, что при умелом составлении «маскирующего» послания, невозможно определить, скрыта ли вообще в послании какая-либо секретная информация. Ниже приведены пример «невинного» послания и скрытого в нем послания.
Для следующего варианта шифрования с помощью решетки Кардано также необходим прямоугольный или (чаще) квадратный трафарет, в котором определенным (не совсем случайным образом, в этом случае уже появляются определенные требования) вырезаны квадратные отверстия (некоторые из них могут иметь общую как сторону, так и вершину). Причем размеры сторон этого трафарета должны быть четными (содержать по четному количеству квадратиков, в каждом из которых помещается ровно одна буква). Прорезанные в трафарете отверстия должны быть расположены таким образом, чтобы при поворотах на 90 0 (или же на 180 0 или при осевых симметрия, в зависимости от формы трафарета и вкусов переписчиков) никакие два отверстия не перекрывались (ни полностью, ни частично). Для квадрата проще всего этого добиться, используя так называемый конструктор решеток Кардано (ниже приведён конструктор решеток Кардано для квадрата со стороной 8). Трафарет можно мысленно разделить на четыре одинаковых квадрата (если трафарет квадратный) или прямоугольника (если трафарет прямоугольный), и отверстия вырезать только в одном из квадратов или прямоугольников.
Когда трафареты (по количеству переписчиков) готовы, шифрование текста происходит так. Берем разлинованный лист бумаги по размеру трафарета. Накладываем на него решетку Кардано. Последовательно в пустые ячейки вписываем часть текста послания, которое хотим зашифровать. Покажем, как шифровать на примере фразы «Шифрование с помощью решетки Кардано» (решетку берем из предыдущего примера).
Затем решетку поворачиваем на 90 0 или 180 0 (в зависимости от формы трафарета и от расположения отверстий, об этом переписчики договариваются заранее, при изготовлении трафарета). В образовавшиеся пустые клетки опять вписываем часть текста послания (уже следующую).
Далее решетку Кардано убираем и клетки, оставшиеся пустыми, заполняем «мусором»: различными буквами, знаками препинания, цифрами (в произвольном порядке, чем хаотичнее, тем лучше).
Конечно, по внешнему виду такого послания понятно, что в нем содержится какая-то секретная информация. Но содержащаяся в послании посторонняя информация («мусор», которым мы заполняли оставшиеся ячейки) делает невозможным взлом этого шифра для злоумышленника. Да и в отличие от предыдущего способа шифрования этот метод прост в использовании и не требует незаурядных литературных способностей. Единственным минусом является нерациональность шифрования: передаваемая информация увеличивается в два, а то и более, раза (за счет того, что в трафарете прорези сделаны так, что после заполнения ячеек посланием, много ячеек остаются пустыми и заполняются случайными символами). К тому же годится этот метод для шифрования сравнительно коротких посланий.
Последний из методов шифрования с помощью решетки Кардано в чем-то похож на предыдущий. Принципиальным отличием от предыдущего способа шифрования является расположение отверстий в трафарете: отверстия должны быть прорезаны так, чтобы при поворотах они замещали ВЕСЬ трафарет, но при этом не накладывались друг на друга (ни полностью, ни частично). Вот здесь без конструктора решеток Кардано будет тяжеловато. Для квадратных трафаретов со стороной 2 такая решетка единственная. Однако при увеличении размеров трафарета количество таких решеток резко возрастает (в квадрате со стороной 8 «помещается» более 4 миллиардов различных решеток Кардано), и определить, какой именно решеткой пользовались для шифрования, невозможно.
Конечно, этот метод прост и удобен в использовании, не требует особых литературных умений и способностей, не увеличивает путем засорения размер передаваемого послания. НО этот шифр является простым перестановочным шифром, который поддается взлому (например, с помощью частотного анализа). Поэтому этот метод шифрования может быть использован либо только в комбинации с каким-либо другим шифром, не поддающимся частотному анализу, либо для передачи информации, на расшифрование которой не будут направлены серьезные ресурсы.
Рассмотрим, наконец, что же такое конструктор решеток Кардано. На рисунке ниже приведен конструктор решеток Кардано для квадрата со стороной 8.
Вопрос первый. Зачем нужен конструктор решеток и почему без него нельзя обойтись? Как уже отмечалось ранее, какие попало ячейки вырезать нельзя. Эти ячейки не должны накладываться друг на друга при поворотах. А при шифровании третьим способом они, помимо этого, должны еще и при поворотах замещать весь трафарет. Этого добиться не так-то легко.
Вопрос второй. Как пользоваться конструктором решеток? Нетрудно заметить, что каждая из клеток конструктора имеет номер от 1 до 16, причем любое число от 1 до 16 является номером ровно четырех ячеек. Чтобы получить решетку Кардано для шифрования вторым способом нужно вырезать клетки таким образом, чтобы среди вырезанных клеток не было клеток с одинаковыми номерами и клетки нескольких номеров (желательно, чтобы количество этих номеров было от 5 до 9) остались невырезанными (каждая из четырех соответствующих клеток). Клетки с этими номерами и останутся пустыми после вписывания послания. Чтобы получить решетку Кардано для шифрования третьим способом необходимо вырезать клетки так, чтобы для каждого номера была вырезана ровно одна клетка (имеющая этот номер).
Вопрос третий. А как же получен этот конструктор и почему он «работает»? Каждая из клеток при поворотах переходит только в строго определенные клетки, назовем эти клетки особыми для данной клетки. Более того, данная клетка и особые для нее клетки при поворотах переходят друг в друга, никак не затрагивая при этом остальные клетки. Такие клетки в конструкторе решеток имеют одинаковый номер. Поэтому если среди вырезанных клеток не будет клеток с одинаковыми номерами, то и наложений не получится. А поскольку все клетки с одинаковым номером переходят друг в друга при поворотах, то если вырежем по одной клетке каждого номера, при поворотах вырезанные клетки замостят весь трафарет. Поэтому можно и самому составить конструктор решеток для произвольного квадрата с четной стороной. Для этого достаточно представить, какие клетки переходят в какие при поворотах.
Криптография в интересах государства
Выше были рассмотрены, можно сказать, примеры шифров «любительского уровня». В профессиональном же смысле шифрование применялось и применяется для защиты информации – государственной, военной, коммерческой. Особое значение криптография приобретала во время войн. Во время Первой мировой войны криптография стала признанным боевым инструментом. Разгаданные сообщения противников вели к ошеломляющим результатам. Перехват телеграммы немецкого посла Артура Циммермана американскими спецслужбами привел к вступлению США в боевые действия на стороне союзников. Вторая мировая война послужила своеобразным катализатором развития компьютерных систем — через криптографию. Использованные шифровальные машины (немецкая «Энигма», английская «Бомба Тьюринга») ясно показали жизненную важность информационного контроля. ( Шифратор — в криптографии устройство для автоматического шифрования. Электромеханические шифраторы появляются в начале 1920-х годов в США и Европе и широко используются вплоть до 1980-х годов, когда распространение получают шифры, предназначенные для использования с вычислительной техникой). В послевоенное время правительства многих стран наложили мораторий на использование криптографии не в военных целях. Ключевые работы публиковались исключительно в виде секретных докладов — таких, как, например книга Клода Шеннона «Теория связи в секретных системах», подходящая к криптографии как к новой математической науке.
Правительственная монополия рухнула только в 1967 году с выходом книги Дэвида Кана «Взломщики кодов». Книга подробно рассматривала всю историю криптографии и криптоанализа. После ее публикации в открытой печати стали появляться и другие работы по криптографии. В это же время сформировался современный подход к науке, четко определились основные требования к зашифрованной информации: конфиденциальность, неотслеживаемость и целостность. Криптография была разделена на две взаимодействующие части: криптосинтез и криптоанализ. То есть криптографы обеспечивают информации защиту, а криптоаналитики, напротив, ищут пути взлома системы.
Современные стандарты шифрования.
Однако целью криптографического протокола зачастую является не только сохранение информации в тайне от посторонних. Участники криптографического протокола могут быть близкими друзьями, у которых нет друг от друга секретов, а могут являться настолько непримиримыми врагами, что каждый из них отказывается сообщить другому, какое сегодня число. Тем не менее, им может понадобиться поставить подписи под совместным договором или удостоверить свою личность. В данном случае нужен криптографический протокол, чтобы предотвратить или обнаружить подслушивание посторонними лицами, не являющимися участниками протокола, а также не допустить мошенничества. Поэтому часто требуется, чтобы криптографический протокол обеспечивал следующее: его участники не могут сделать или узнать больше того, что определено протоколом.
Криптоанализ — наука о методах получения исходного значения зашифрованной информации.
Хотя понятие криптоанализ было введено сравнительно недавно, некоторые методы взлома были изобретены десятки веков назад. Первым известным письменным упоминанием о криптоанализе является «Манускрипт о дешифровке криптографических сообщений», написанный арабским учёным Аль-Кинди ещё в 9 веке. В этом научном труде содержится описание метода частотного анализа.
Частотный анализ — основной инструмент для взлома большинства классических шифров перестановки или замены. Данный метод основывается на предположении о существовании нетривиального статистического распределения символов, а также их последовательностей одновременно и в открытом тексте, и в шифротексте. Причём данное распределение будет сохраняться с точностью до замены символов, как в процессе шифрования, так и в процессе дешифрования. Стоит отметить, что при условии достаточно большой длины шифрованного сообщения моноалфавитные шифры легко поддаются частотному анализу: если частота появления буквы в языке и частота появления некоторого присутствующего в шифротексте символа приблизительно равны, то в этом случае с большой долей вероятности можно предположить, что данный символ и будет этой самой буквой. Самым простым примером частотного анализа может служить банальный подсчёт количества каждого из встречающихся символов, затем следуют процедуры деления полученного числа символов на количество всех символов в тексте и умножение результата на сто, чтобы представить окончательный ответ в процентах. Далее полученные процентные значения сравниваются с таблицей вероятностного распределения букв для предполагаемого языка оригинала. Но существует некоторая разница значений частот, которая объясняется тем, что частоты существенно зависят не только от длины текста, но и от характера текста. Например, текст может быть технического содержания, где редкая буква Ф может стать довольно частой. Поэтому для надежного определения средней частоты букв желательно иметь набор различных текстов.
Атака по ключам. Одной из причин ненадёжности криптосистем является использование слабых ключей. Фундаментальное допущение криптоанализа, впервые сформулированное О. Кирхгоффом, состоит в том, что секретность сообщения всецело зависит от ключа, т.е. весь механизм шифрования, кроме значения ключа, известен противнику (секретность алгоритма не является большим препятствием: для определения типа программно реализованного криптографического алгоритма требуется лишь несколько дней инженерного анализа исполняемого кода). Слабый ключ – это ключ, не обеспечивающий достаточного уровня защиты или использующий в шифровании закономерности, которые могут быть взломаны. Обычно считается, что алгоритм шифрования должен по возможности не иметь слабых ключей. Если это невозможно, то количество слабых ключей должно быть минимальным, чтобы уменьшить вероятность случайного выбора одного из них. Тем не менее, все слабые ключи должны быть заранее известны, чтобы их можно было отбраковать в процессе создания ключа.
Бандитский криптоанализ. Многие современные методы шифрования настолько устойчивы к взлому, что приходится использовать и такой «метод» взлома шифра. Криптоаналитик может использовать так называемый «человеческий фактор», то есть пытаться с помощью шантажа, подкупа, пыток или иных способов получить информацию о системе шифрования или даже сам ключ шифрования. Например, дача взятки, как одна из разновидностей бандитского криптоанализа, может носить название «Вскрытие с покупкой ключа». Таким образом, методика вскрытия построена на слабости людей как составной части системы защиты информации. Бандитский криптоанализ считается очень мощным способом взлома системы, а зачастую и наилучшим путём вскрытия шифров.
Возникает вопрос: если прогресс в области разработки новых методов взлома велик, почему мы продолжаем использовать криптосистемы, чья стойкость постоянно снижается? Ещё во времена Второй Мировой войны основоположник современной криптографии Клод Шеннон доказал существование принципиально не раскрываемых шифров – совершенно секретных систем, в которых ключ, «накладываемый» на текст, не может использоваться повторно, а его размер больше либо равен объёму текста. Дело в том, что использование способа шифрования, получившего название «одноразовых блокнотов», в большинстве случаев оказывается слишком дорогим и неоправданным. Нет смысла бороться за устойчивость системы защиты информации к взлому ниже некоторой «фоновой» вероятности, когда на другой чаше весов оказываются такие характеристики криптосистемы, как стоимость, сложность реализации и скорость доступа к зашифрованному тексту. Выбор необходимой степени защиты – это поиск компромисса между уровнем безопасности и расходами на ее обеспечение. Таким образом, разработка новых методов криптоанализа с последующей публикацией и открытым обсуждением результатов является основным двигателем современной криптографии.
Вопросы, связанные с представлением информации для возможности её технической обработки и интерпретации, т.е. кодирования с помощью некоторого набора символов (алфавита) очень интересны для исследования. Ведь на самом деле, любой человек в современном обществе достаточно значимую часть информации получает именно в закодированном виде, будь то книга, компьютерное представление символьной информации и т.п. А сами технические устройства могут «понять» информацию только в виде кодов. Поэтому интересно исследовать и историю кодирования, и современное состояние вопроса, и постараться в будущем, возможно, самому принять участие в разработке систем кодирования и обработки информации.
Что же касается криптографии и криптоанализа. Весьма интересным приложением криптографических методов может быть также их применение для дешифровки древних языков, а также тайнописей, не разгаданных до сих пор (например, «Письмо Войнича», «Письмо в Кодексе Рохонци», «Письмо Серафини», медицинские тайнописи (врачебные алфавиты), не дешифрованные до сих пор «тарабарские грамоты»).
Коробейников А. Г. Математические основы криптографии. Учебное пособие. СПб: СПб ГИТМО (ТУ), 2002.