дирекционный угол линии равен 1250 чему равен румб данной линии
Дирекционные углы и осевые румбы



Лекция 6
Ориентирование линии. Прямая и обратная геодезические задачи.
При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.
Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.
В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.
Дирекционные углы и осевые румбы
Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).
Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.
Рис. 16. Дирекционные углы
Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.
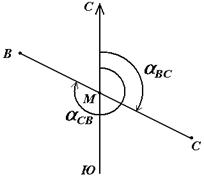
В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим αBC является прямым дирекционным углом линии ВС в точке М, а угол αCB – обратным дирекционным углом этой же линии в той же точке.
Рис. 17. Прямое и обратное направление линии
Из рисунка видно, что αCB = αBC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.
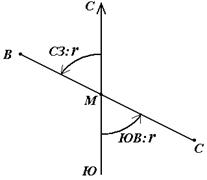
Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).
Осевым румбомназывается острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.
Рис. 18. Румбы и дирекционные углы
Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).
Зависимость между дирекционными углами и румбамиопределяется для четвертей по следующим формулам:
I четверть (СВ) r = α
II четверть (ЮВ) r = 180° – α
III четверть (ЮЗ) r = α – 180°
IV четверть (СЗ) r = 360° – α
Дирекционные углы линий. Прямая геодезическая задача. Составление топографического плана участка местности
Страницы работы
Фрагмент текста работы
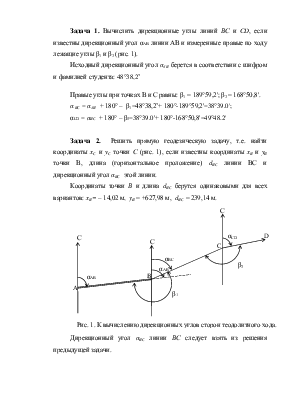
Задача 1. Вычислить дирекционные углы линий ВС и CD, если известны дирекционный угол αАВ линии АВ и измеренные правые по ходу лежащие углы β1 и β2 (рис. 1).
Исходный дирекционный угол αАВ берется в соответствии с шифром и фамилией студента: 48°38,2’
Правые углы при точках В и С равны: β1 = 189°59,2′; β2 = 168°50,8′.
Задача 2. Решить прямую геодезическую задачу, т.е. найти координаты хС и уС точки С (рис. 1), если известны координаты хВ и уB точки В, длина (горизонтальное проложение) dBС линии ВС и дирекционный угол αВС этой линии.
Координаты точки В и длина dВС берутся одинаковыми для всех вариантов: хВ = – 14,02 м, yB = +627,98 м, dВС = 239,14 м.
Дирекционный угол αВС линии ВС следует взять из решения предыдущей задачи.
Координаты точки С вычисляются по формулам:
yС = yВ + ΔyВС=+627,98+149,36=+777,34 м, где ΔхВС и ΔуВС — приращения координат, вычисляемые из соотношений:
Составление топографического плана участка местности
По данным полевых измерений составить и вычертить топографический план участка в масштабе 1: 2000 с высотой сечения рельефа 1 м. Решить отдельные задачи.
Работа состоит из следующих этапов: обработка ведомости вычисле-ния координат вершин теодолитного хода; обработка тахеометрического журнала; построение топографического плана; решение задач по топографическому плану.
Исходные данные и задания
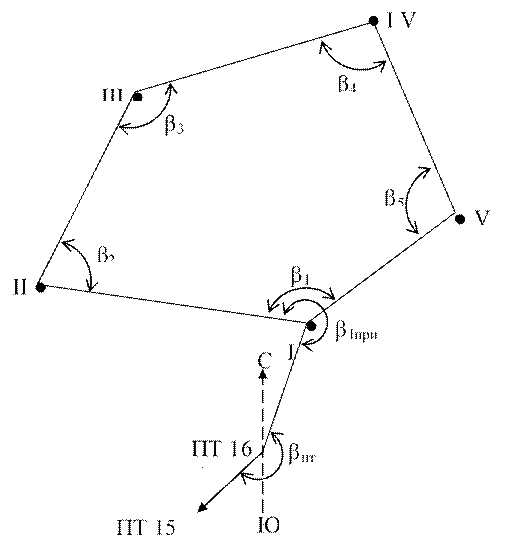
1. Для съемки участка на местности был проложен замкнутый высотно-теодолитный ход I, II, III, IV и V с привязкой к пунктам ПТ 15 и ПТ 16 Государственной геодезической сети (рис. 2). В нем были измерены длины всех сторон, а также на каждой вершине хода — правый по ходу горизонтальный угол и углы наклона на предыдущую и последующую вершины.
Измерение углов производилось теодолитом 2Т30.
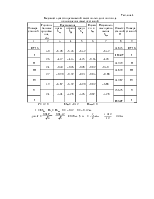
Результаты полевых измерений по теодолитному ходу горизонталь-ных углов β, углов наклона ν и линий S занесены в табл. 1, а по тахеометрическому ходу занесены в табл. 5. Как одни, так и другие результаты являются общими для всех вариантов.
Рис. 2. Схема высотно–теодолитного хода съемочного обоснования
Результаты полевых измерений по высотно-теодолитному ходу
Известны координаты пунктов триангуляции ГГС ПТ 15 и ПТ 16, которые выбираются из табл.2 по последней цифре шифра и количества букв в фамилии студента: координаты Х и У опорных пунктов равны величинам таблицы в строке, соответствующей последней цифре шифра, за исключением координаты Х ПТ15, значение которой увеличивается на величину произведения количества букв в фамилии студента на 100.
Координаты опорных точек ПТ15 и ПТ16
3. Отметка пункта ПТ 16 обычно известна из геометрического нивелирования. При выполнении же задания значение отметки ПТ 16 следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра студента. В дробной части отметки (дм, см, мм) повторяются цифры, что и в целой части.
Вычисление координат съемочного обоснования
Увязка углов хода. Значения измеренных углов и величины горизонтальных проложений записывают в графу 2 и 7 ведомости вычисления координат (табл. 3). Вычисляют сумму Σβпр. измеренных углов замкнутого хода (полигона). Определяют теоретическую сумму углов Σβт = 180 0 (n – 2), где n — число вершин хода.
Примечание. При нахождении суммы Σβпр. используются только внутренние углы пятиугольника. Углы висячего хода на точках ПТ16 и ст. I (βПТ и β1прим ) в данной задаче не увязываются.
Если невязка fβне превышает допустимой величины доп. fβ = ±1′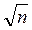
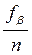
После этого приступают к вычислению дирекционных углов и румбов сторон хода. Для этого необходимо знать исходный дирекционный угол α0, для чего решается обратная геодезическая задача.
Отсюда искомый дирекционный угол линии 15 – 16 будет равен:
Перевод дирекционных углов в румбы
| Номер четверти | Название четверти | Формула перевода |
| I | СВ | rI=α |
| II | ЮВ | rII=180º-α |
| III | ЮЗ | rIII=α-180º |
| IV | СЗ | rIV=360º-α |
Координаты точки п/п83 вычисляют по формулам
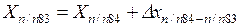
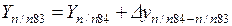
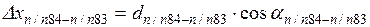
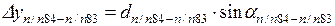
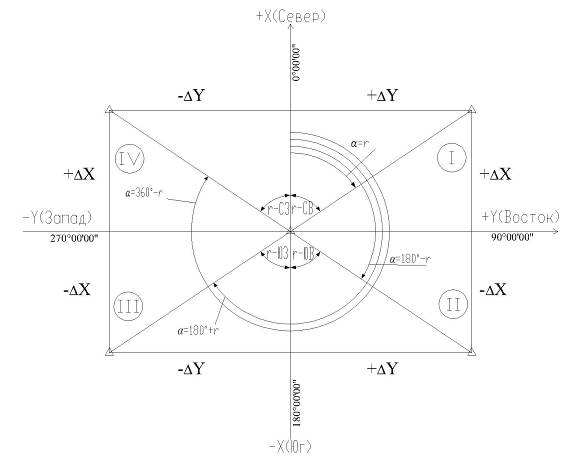
Для удобства вычислений дирекционный угол можно предварительно перевести в румб, пользуясь рис. 1.2 и табл. 1.1.
Рис. 1.2. Зависимость между дирекционными углами и румбами
При использовании румбов знак приращений координат ставят в соответствии с названием румба (табл. 1.2).
Знаки приращений прямоугольных координат
| Приращения | Названия румбов | |||
| СВ | ЮВ | ЮЗ | СЗ | |
| ∆x | + | — | — | + |
| ∆y | + | + | — | — |
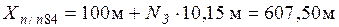
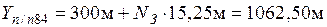
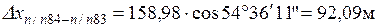
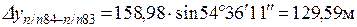
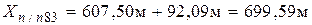
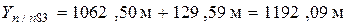
Обработка результатов топографической съемки
Участка местности
Исходные данные. Для съемки участка на местности проложен высотно-теодолитный ход между двумя пунктами полигонометрии п/п84 и п/п83. Схема сети и результаты полевых измерений выдаются преподавателем и являются общими для всех вариантов. Для примера, рассмотренного в учебно-методическом пособии, схема сети приведена на рис. 1.3. В ходе измерены длины линий и горизонтальные углы, лежащие справа по ходу. Результаты измерения горизонтальных углов и длин линий для сети, изображенной на рис. 1.3, приведены в табл. 1.3.
Дата добавления: 2016-01-09 ; просмотров: 4607 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Связь между дирекционными углами и горизонтальными углами



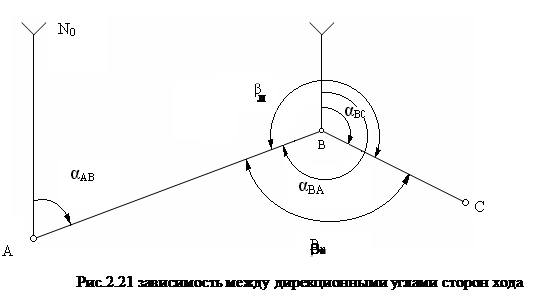
Пусть имеем две стороны хода АВ и ВС (рис.2.21). Дирекционный угол aАВ стороны АВ будем считать известным. Если правый по ходу угол обозначить βn, то
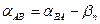
Подставляя значение 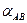
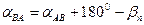
Если бы мы имели при т.В не правый, а левый угол βл, то получили бы формулу:
 |
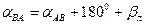
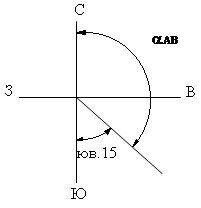
Пример N°1. Дирекционный угол линии АВ равен 165°. Найти румб.
Решение: По формулам взаимосвязи азимутов и румбов получим
Пример N°2. Определить дирекционный угол линии АВ, если Аu=60°30’; γ =+0°10’.
Решение: Дирекционный угол линии АВ равен
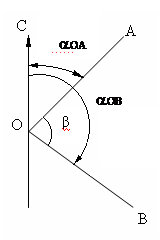
Пример N°3. Определить величину угла β, если даны дирекционные углы линий aОА=30°00′; aов=135°00′
Угол β составит:
Пример №4. Вычислить дирекционный угол a2-3 и её румб, если a1-2=60° β2прав=140°

Вопросы для самоконтроля :
1. Что такое широта и долгота?
2. Как по карте определить географические координаты точки?
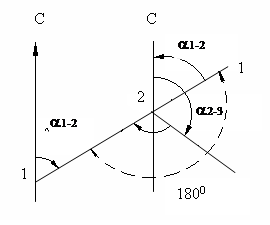
3. Что представляет собой зональная система прямоугольных координат?
4. Как по карте определить прямоугольные координаты точки?
5. Что называется ориентированием линии на местности?
6. Что называется истинным азимутом линии местности?
7. Что называется магнитным азимутом линии местности?
8. Что называется дирекционным углом линии местности?
9. Как связаны между собой углы ориентирования?
10. На сколько отличаются прямой дирекционный угол от обратного?
11. Как перейти от дирекционного угла к румбу?
12. Как с помощью транспортира измерить на карте дирекционный угол линии местности?
13. Как связаны дирекционные углы и горизонтальные углы?
14. Как связаны дирекционные углы и прямоугольные координаты?
План конспект по геодезии на тему «Ориентирование линий»
Министерство образования и науки Республики Башкортостан
Башкирский колледж архитектуры, строительства и коммунального хозяйства
по дисциплине «Основы геодезии»
на тему «Ориентирование линий»
Для студентов специальности 08.02.01
Строительство и эксплуатация зданий и сооружений
Тема «Ориентирование линий»
1. Дирекционные углы линий.
3. Зависимость дирекционных углов и румбов.
4. Методика решения задач на определение примычных углов.
1. Дирекционные углы линий.
Определение положения линий относительно сторон света называется ориентированием.
Ориентирование заключается в том, что определяется угол между исходным направлением и данной линией.
За исходное направление для ориентирования принимают ось абсцисс (ось Х) или меридиан.
Для ориентирования линий служат углы, которые называются дирекционными углами и румбами.
Угол, составленный северным концом меридиана и данной линией, называется дирекционным углом.
Дирекционный угол обозначается ℒ
 |
 |
Дирекционный угол отсчитывается
от 0 до 360˚ по ходу часовой стрелки.



Построить угол, образованный двумя линиями, имеющими следующие дирекционные углы
и определить величину этого угла.

 |









 |



 |
300 о – 180 о = 120 о
 |
 |
Прямой дирекционный угол отличается
Иногда для ориентирования линии на местности пользуются не дирекционными углами, а румбами.
Угол, составленный ближайшим концом меридиана и данной линией, называется румбом.
 |
 |
Румб имеет значение
от 0 до 90˚ и направление, в зависимости от четверти, в которой находится данная линия



 |

 З 1 В
З 1 В
 |
 |
Построить угол, образованный двумя линиями, имеющими следующие румбы
и определить величину этого угла.











 |
 |
Прямой румб отличается
от обратного только направлением
3. Зависимость дирекционных углов и румбов.
На практике часто возникает необходимость определить румбы линий по дирекционным углам и наоборот.
Таблица зависимости румбов и дирекционных углов.
Пример перевода дирекционных углов в румбы
1. если дирекционный угол α равен 42°, тогда согласно таблицы румб вычисляется по формуле r=α=42°, а название румба будет СВ;
2. если дирекционный угол α равен 100°, тогда согласно таблицы румб вычисляется по формуле r=180°-α=180°-100°=80°, а название румба будет ЮВ; r = ЮВ: 80
3. если дирекционный угол α равен 210°, тогда согласно таблицы румб вычисляется по формуле r=α-180°=210°-180°=30°, а название румба будет ЮЗ; r = ЮЗ: 30
4. если дирекционный угол α равен 335°, тогда согласно таблицы румб вычисляется по формуле r=360°-α=360°-335°=25°, а название румба будет СЗ.
4.Методика решения задач на определение примычных углов.
1. Через вершину примычного угла, который необходимо вычислить, провести меридиан, показать направление север и юг.
2. Определить, какими линиями составлен примычный угол.
3. Показать известные румбы или дирекционные углы этих линий на чертеже.
4. Вычислить примычный угол.



 |



 |

 |

Домашнее задание
1. Построить линии по заданному дирекционному углу
2. Провести линии по заданным румбам.
3. По заданному дирекционному углу определить румб линии
4. По заданному румбу линии определить дирекционные углы
5. Построить угол, образованный двумя линиями, имеющими следующие румбы r 1-2 = СВ:50˚, r 2-3 = ЮВ:30˚, и определить величину этого угла.















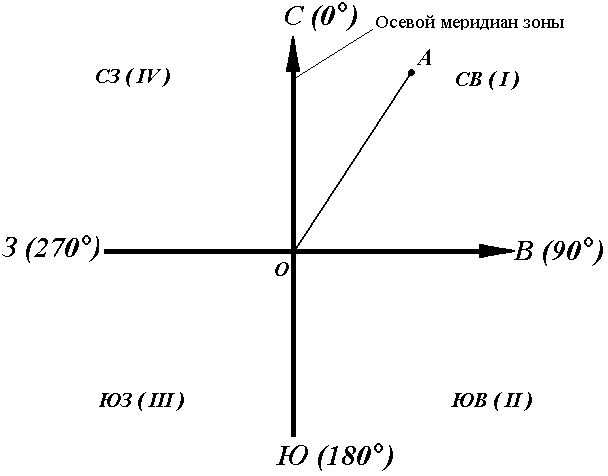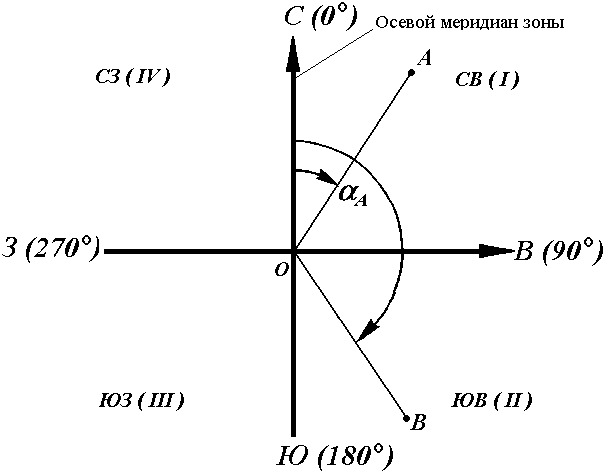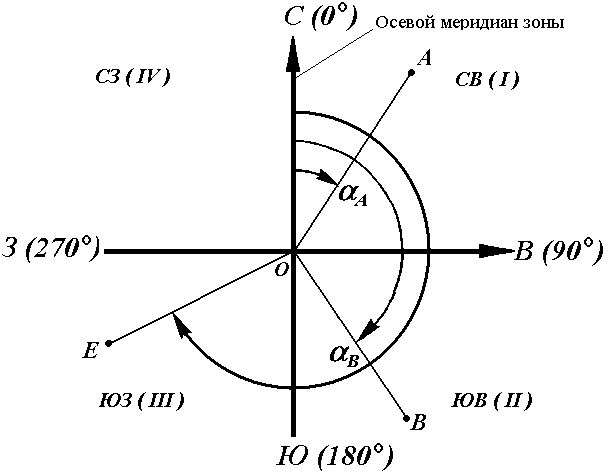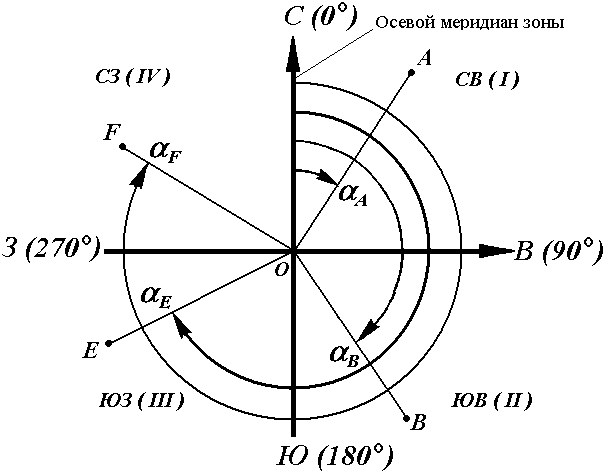




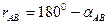
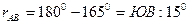
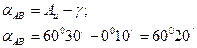
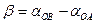
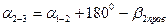
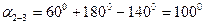
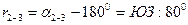





 З 1 В
З 1 В





