дискриминант это что простыми словами

Общие сведения

Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.

Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные. При этом, найдя их, определить первоначальные уже не составляет труда.

Такой способ был применён и к квадратному уравнению. Благодаря ему стало возможным упростить квадратичную форму с двумя переменными, используя дискриминант. Это понятие тесно связано с многочленом, имеющим следующий вид: d (m) = a 0 *m n + a 1 *m n-1 + a 2 *m n-2 + … + a n-1 *m + a n, где m — искомое неизвестное, a n, a n-1, a n-2, … a 1 и a 0 — числовые постоянные.

Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий». Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных.

При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.

Смысл дискриминанта

Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.

Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m 2 + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m 2 + 2m +1 — 1- 8 = 0. Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.

В общем виде все эти преобразования можно выполнить в следующей последовательности:

Многочлен b2 — 4ac было решено принять за дискриминант. Это выражение по сути и определяет возможность существования решений и количество корней. Выполнив его расчёт, фактически и находится ответ уравнения.

Взаимосвязь параметра

Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a > 0, и вниз, если a 2 — 4 ac к удвоенному произведению первого коэффициента в уравнениях x1 = (- b + √ b 2 — 4 ac) / 2a; x2 = (- b — √ b 2 — 4 ac) / 2a. Подкоренное выражение называют формулой сокращённого дискриминанта.

Дискриминант при нахождении корней уравнения может принимать три значения:

Последнее выражение является формулой корней квадратного уравнения. Именно с её помощью могут решаться равенства, в степени которых стоит двойка. Через дискриминант можно вычислять корни и уравнений больших порядков. Для этого используются приёмы понижения степени до квадратного. Но эти операции учащиеся начинают изучать на уроках в выпускном классе, когда проходят решение уравнений n-го порядка.

Типовые примеры

Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:

Определить возможность решения уравнения 4m 2 — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m 2 — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.

Таким образом, любое выражение нужно стремиться переписать так, чтобы оно приняло классический вид. Это может быть умножение или деление на какое-либо число, поиск общего знаменателя. А уже после нужно искать дискриминант, по виду которого можно определить, есть ли смысл в дальнейшем нахождении корней уравнения.

Вычисления на онлайн-калькуляторе

Поиск решений уравнения через дискриминант — довольно простая тема. Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.

Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.

Из сервисов, предлагающих такие услуги, можно отметить:

Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.

Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.

Источник

Квадратное уравнение. Дискриминант. Теорема Виета.

теория по математике 📈 уравнения

Уравнение вида ax 2 +bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.

Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.

Дискриминант

Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).

Нахождение корней квадратного уравнения

Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:

D=b 2 –4ac

Пример №1. Решить уравнение х 2 –2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b 2 –4ac=(–2) 2 –41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:

Пример №2. Решить уравнение 5х 2 +2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b 2 –4ac=2 2 –4=4–20=–16, D 2 –6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.

D=b 2 –4ac=(–6) 2 –4=36–36=0, D=0, 1 корень

Теорема Виета

Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.

Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.

Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.

Пример №4. Решить уравнение х 2 –10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:

Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.

Пример №5. Решить уравнение: х 2 +5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:

Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:

Источник

Дискриминант

Дискримина́нт многочлена , есть произведение

, где — все корни (с учётом кратностей) в некотором расширении основного поля, в котором они существуют.

Содержание

Свойства

Примеры

История

Примечания

Полезное

Смотреть что такое «Дискриминант» в других словарях:

ДИСКРИМИНАНТ — перекись твою Ньютона! Жарг. студ. Бран. шутл. Выражение досады, раздражения. Вахитов 2003, 48 … Большой словарь русских поговорок

дискриминант — а, м. discriminant m. <лат. discriminare разделять, отделять. мат. Составленное из величин, определяющих заданную функцию. выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы, напр. д. многочлена равен … Исторический словарь галлицизмов русского языка

дискриминант — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN discriminant … Справочник технического переводчика

дискриминант — (лат. discriminans (dis criminantis) различающий, разделяющий) мат. составленное из величин, определяющих заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы, напр. д. многочлена равен… … Словарь иностранных слов русского языка

дискриминант — квадратного уравнения ах2 + bx + с = 0, выражение b2 – 4ас = D, по знаку которого судят о наличии у этого уравнения действительных корней (D≥0). * * * ДИСКРИМИНАНТ ДИСКРИМИНАНТ квадратного уравнения ax2 + bx + c = 0 выражение b2 – 4ac = D, по… … Энциклопедический словарь

дискриминант — diskriminantas statusas T sritis fizika atitikmenys: angl. discriminant vok. Diskriminant, m rus. дискриминант, m pranc. discriminant, m … Fizikos terminų žodynas

Дискриминант — (от лат. discriminans разделяющий, различающий) многочлена P (x) = a0xn + a1xn 1 +. + an, выражение D = a02n 2Пi … Большая советская энциклопедия

дискриминант — дискриминант, дискриминанты, дискриминанта, дискриминантов, дискриминанту, дискриминантам, дискриминант, дискриминанты, дискриминантом, дискриминантами, дискриминанте, дискриминантах (Источник: «Полная акцентуированная парадигма по А. А.… … Формы слов

Источник

Значение слова дискриминант

Дискриминант в словаре кроссвордиста

дискриминант

Дискриминант Дискримина́нт многочлена formula_1, formula_2, есть произведение Чаще всего используется дискриминант квадратного трёхчлена, знак которого определяет количество действительных корней. Во всех следующих примерах рассматриваются многочлены с вещественными коэффициентами и отличным от нуля старшим коэффициентом.

(лат. discriminans (dis-criminantis) различающий, разделяющий) мат. составленное из величин, определяющих заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы, напр. д. многочлена равен нулю тогда и только тогда, когда у многочлена есть равные корни.

Новый словарь иностранных слов

[мат. составленное из величин, определяющих заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы, напр. д. многочлена равен нулю тогда и только тогда, когда у многочлена есть равные корни.

Словарь иностранных выражений

Словарь русского языка Лопатина

Современный толковый словарь, БСЭ

Полный орфографический словарь русского языка

функция коэффициентов многочлена, позволяющая определить его корни

Источник

ДИСКРИМИНАНТ

Д. равен нулю тогда и только тогда, когда многочлен имеет кратные корни. Д. симметричен относительно корней многочлена и поэтому может быть выражен через его коэффициенты.

Лит.:[1] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975.

Пусть k=Q— поле рациональных чисел, К- поле алгебраич. чисел и М- некоторый модуль ранга пв К. Тогда для любых двух базисов модуля Мзначения Д. совпадают и это общее значение Д. наз. дискриминантом модуля М. Если Мсовпадает с кольцом целых чисел поля К, то Д. модуля Мназ. просто дискриминантом поля К и обозначается D_k. Число D_k, является важной характеристикой поля К. Напр., если Кдопускает s вещественных и 2t комплексных вложений в поле комплексных чисел С, то

где z_k(q)- дзета-функция Дедекинда, h- число классов дивизоров, R— регулятор поля К и т— число корней из единицы в поле К. Имеется оценка

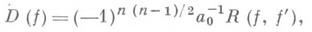
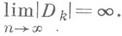которая показывает, что Для квадратичного поля 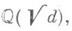где d- свободное от квадратов целое рациональное число, 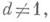имеют место формулы:

Лит.:[1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Ленг С, Алгебраические числа, пер. с англ., М., 1966; [3] 3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 1, М., 1963; [4] Джекобсон Н., Теория колец, пер. с англ., М., 1947.

Лит.:[1] Джекобсон Н., Теория колец, пер. с англ., М., 1947.

Источник

• ← картинки для оформления стены в комнате
• главный музейный комплекс эрмитажа что включает в себя билет →