глубина сжимаемой толщи что это
Комментарий 2-го предложения 1-го абзаца п.5.6.41 СП…
Там идет речь о минимальной глубине сжимаемой толщи (учитывается в расчете осадок).
Рассматривается ТРИ ситуации:
1) ЕСЛИ ширина фундамента в диапазоне [ 0
искусственные сооружения на дорогах
Это похоже на правду.
Понизили Hc не только на прочные грунты (с 0,2 до 0,5), но и на слабые (с 0,1 до 0,2). Но при этом грунты немного ослабели (уже начиная с Е = 7 МПа).
Почему это похоже на правду:
1) в украинском ДБН Нс характеризуется диапазоном 0,2 – 0,5 (в зависимости от ширины Ф.)
2) метод послойного суммирования в любом случае дает завышенные значения, поскольку не учитывает в полной мере жесткость Ф. и законтурную работу Ф. Общий коэффициент БЕТТА = 0,8, нужный для уменьшения S по вышеуказанным причинам, вероятно не справлялся со своими задачами.
Я верю в 0,5
искусственные сооружения на дорогах
2) метод послойного суммирования в любом случае дает завышенные значения, поскольку не учитывает в полной мере жесткость Ф. и законтурную работу Ф. Общий коэффициент БЕТТА = 0,8, нужный для уменьшения S по вышеуказанным причинам, вероятно не справлялся со своими задачами.
Я верю в 0,5
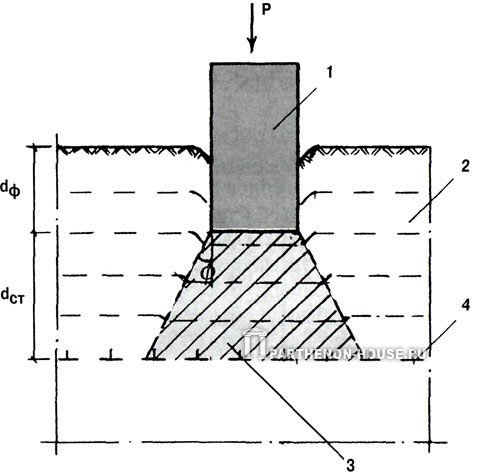
Определение мощности сжимаемой толщи
Другим общим положением для большинства методов расчета осадок является выделение сжимаемой толщи или так называемой активной глубины #а, в пределах которой учитываются деформации грунта. Сжатием глубже расположенных слоев при определении осадок пренебрегают. Тогда величину вертикального смещения любой точки на поверхности основания можно представить в виде
г, 5 или 5+ Н) = ааа2,б, а для случая определения 5 или 5 + Л, как сгг( ст г(^/) = 0,1стг,б-
Рис. 5.3. Определение величины активной глубины сжатия сравнением дополнительных напряжений с бытовыми (а) и по величине структурной прочности (б)
В СНиП П-16—76 «Основания гидротехнических сооружений» граница активной зоны находится из условия, чтобы напряжения от полных внешних нагрузок а2(д) +
+ 5(Т2,б, где а2,б — напряжения от собственного веса столба грунта, отсчитываемого от поверхности дна котлована. В случае однородного грунта ст2,б=Яаугр.
В этом случае не учитывается влияние заглубления фундамента сооружения.
Все эти рекомендации являются весьма условными. Более физически обоснованными являются другие способы, которые, к сожалению, менее разработаны. К ним относится способ, предложенный
В. А. Флориным, где за активную глубину сжатия принимается глубина, при которой пренебрежение сжатием более глубоко расположенных слоев основания приводит к возникновению расчетной погрешности в величине осадки, не превышающей заданной величины.
Весьма логичен способ (рис. 5.3, б), основанный на условии, что в пределах активной глубины, включая его нижнюю границу, аг<д) + + сгг(^) > Остр, где Остр — величина структурной прочности грунта (см. § 1.4).
В последние годы в ряде нормативных документов получил развитие способ определения Яа путем введения ниже Яа условного, несуществующего абсолютно несжимаемого подстилающего слоя — способ линейно деформируемого слоя конечной толщины. Расчетная толщина линейно деформируемого слоя определяется по чисто эмпирической зависимости Яа>рас = Я0.а + Ы, где Ъ — ширина сооруже
ния, м; Н0,а и / — эмпирические величины, принимаемые соответственно равными для оснований, сложенных: глинистыми грунтами — Эми 0,15; песчаными грунтами — 6 м и 0,1. Кроме того, вводятся поправки на интенсивность давления от сооружения умножением Яа.рас на понижающий или повышающий коэффициент (0,8. 1,2). Условность введения в однородной толще грунта подстилающего фиктивного абсолютно несжимаемого слоя очевидна.
Конечно, во всех способах при залегании действительно несжимаемых грунтов в пределах Яа глубина сжимаемого слоя должна ограничиваться кровлей этого грунта. В этом случае применение для расчета осадки слоя конечной толщины с Яа>Рас
61. Расчет многосекционного дома на грунтовом основании
В современной строительной практике часто проектируются и строятся не отдельные здания, а целые комплексы зданий или многосекционные здания, каждая секция которых имеет свой фундамент, что требует учета взаимовлияния зданий друг на друга и накладывает определенные сложности при расчете. ПК ЛИРА 10 позволяет успешно решить эту проблему, более того, можно просчитывать фундаменты, лежащие в разных уровнях.
На примере расчета многосекционного здания (рис. 1) рассмотрим особенности моделирования таких зданий.
Рис. 1. Расчетная модель многосекционного здания
Фундамент этого здания не только разделен на несколько частей деформационными швами, но и имеет различные высотные отметки.
Рассмотрим алгоритм моделирования взаимодействия сооружения с грунтом основания.
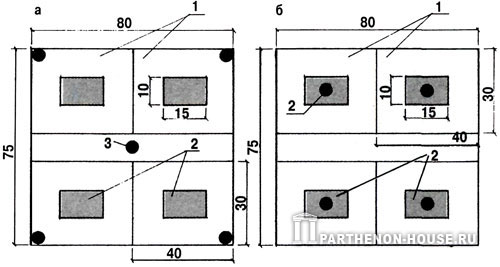
Рис. 2. Задание параметров упругого основания
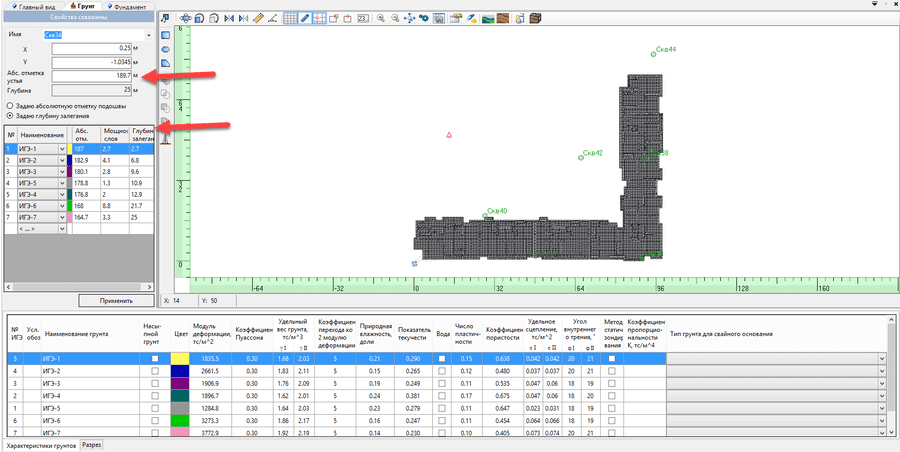
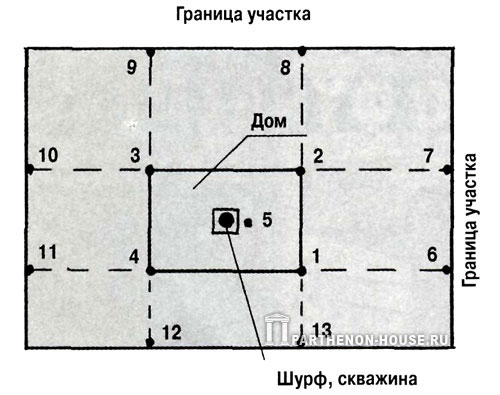
Рис. 3. Задание скважин
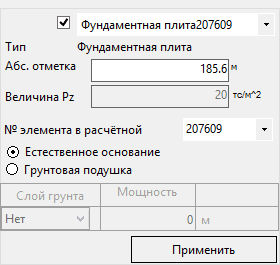
Рис. 4. Задание абсолютной отметки фундамента
Многоуровневость фундаментной плиты программой оценивается автоматически в соответствии с расчетной схемой. При этом, фундаментная плиты может иметь и разрывы, что не повлияет на расчет.
Если сделать разрез, то на нем хорошо видно, что плита имеет разные уровни (рис. 5).
Рис. 5. Разрез по фундаменту
С методами расчета коэффициентов постели можно ознакомится в одной из предыдущих заметок.
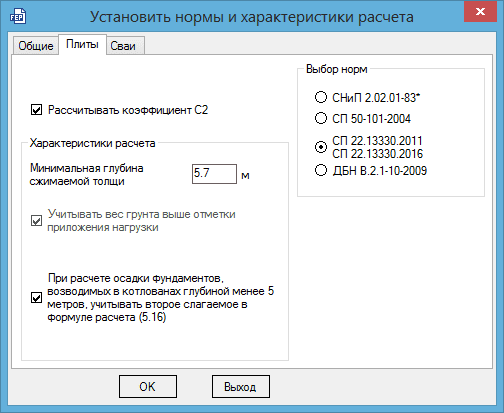
Дополнительно обратим внимание на величину, которую многие пользователи оставляют без внимания, а именно, минимальную глубину сжимаемой толщи (рис. 6).
Рис. 6. Задание характеристик расчета
Минимальная глубина сжимаемой толщи должна быть определена по п. 5.6.41 СП 22.13330.
При этом глубина сжимаемой толщи не должна быть меньше Hmin, равной b/2 при b≤10 м, (4+0,1b) при 10 60 м. Где b – меньшая сторона фундамента.
В нашем примере она составит Hmin=4+0.1b=4+0.1·17=5.7 м.
Как известно, коэффициенты постели дают нам связь только по вертикальному направлению, и, если мы не закрепим модель в горизонтальных направлениях, то программа выдаст нам ошибку о геометрической изменяемости системы. Существует несколько методов закрепления основания: жесткое защемление всей плиты от горизонтальных смещений, закрепление крестом, закрепление упругими связями. Последний метод является более предпочтительным. В рамках данной заметки мы не будем рассматривать подробно плюсы и минусы различных методик, возможно вынесем их в отдельную заметку.
После задания закреплений, можно отправлять задачу на расчет, мы помним, что в начальном приближении задали произвольную нагрузку, после проведения расчета нам нужно уточнить нагрузку на грунт.
Последовательность действий следующая:
При пересчете, ПК ЛИРА 10 задаст вопрос «Параметры грунтового основания необходимо пересчитать. Пересчитать?». Нажимаем «Да».
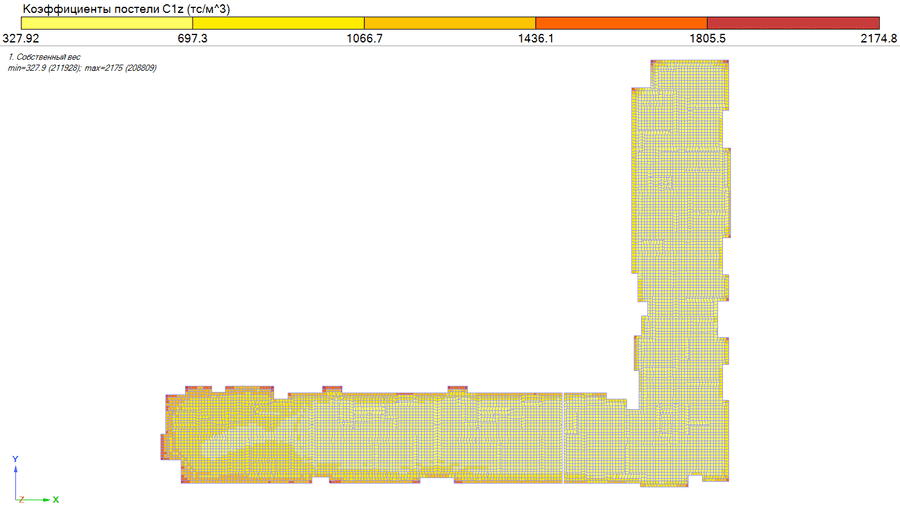
Таких итераций может быть произведено до 6. Критерием остановки тут должны служить коэффициенты постели, а именно, их изменения. Т.е. после очередной итерации коэффициенты не должны значительно изменится. Результаты определения коэффициентов постели приведены на рисунке 7.
Рис. 7. Результаты определения коэффициентов постели.
Если у вас возникли вопросы, вы можете задать их нашим специалистам в чате на сайте, на форуме ЛИРА 10 или в теме обсуждения в социальной сети «Вконтакте»








 кПа.
кПа.
 0,033 м = 3,3 см.
0,033 м = 3,3 см.
 0,035 м = 3,5 см.
0,035 м = 3,5 см.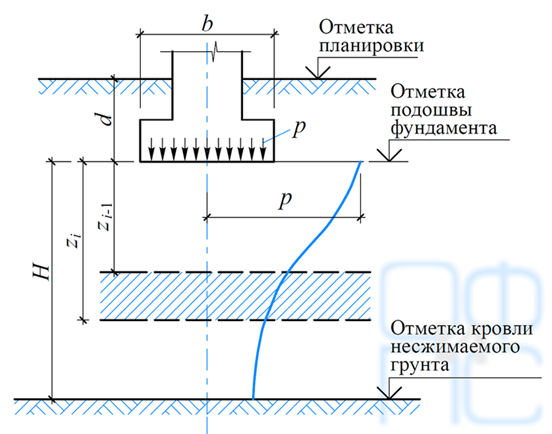
 м = 4 см.
м = 4 см.