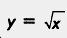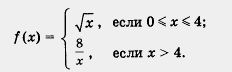график функции что первое х или у
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Парабола, график, вершина, нули.
теория по математике 📈 функции
Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax 2 +bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х 2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
D=b 2 – 4ac=4 2 — 4 ∙ 1 ∙ ( − 5 ) = 36
Значит, нули функции равны –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
А) a>0, с >0 Б) а 0 В) а>0, с
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 — это график №1
Б) а 0 — это график №3
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
pазбирался: Даниил Романович | обсудить разбор | оценить
Линейная функция, ее свойства и график
теория по математике 📈 функции
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
Вписываем в таблицу значения у:
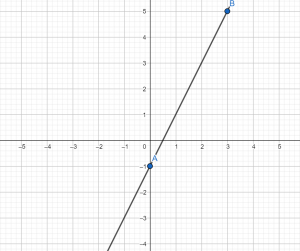
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент — положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
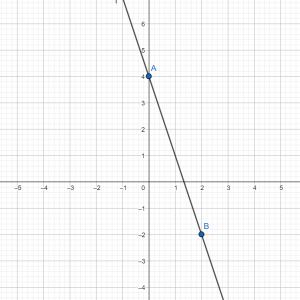
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
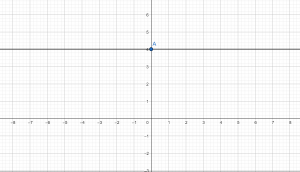
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
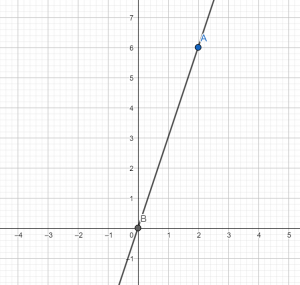
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ассмотрим коэффициенты под №3. Если k 90 0 ) угол с положит.направлением оси абсцисс (Ох). Если b 0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом ( 0 ). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b 0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
График данной функции зависит от k и b.
pазбирался: Даниил Романович | обсудить разбор | оценить
Графики функций и их модификация
Разделы: Математика
Графиком функции у=f(х), где 
Параллельный перенос (сдвиг) вдоль оси абсцисс
График функции у=f(х+а) получаем с помощью параллельного переноса (сдвига) последнего вдоль оси Ох на |а| единиц масштаба в направлении, имеющем знак, противоположный знаку числа а.
Например, для построения графика функции у=f(х+2) вспомогательную ось ординат графика функции у=f(х) переносим параллельно вдоль оси абсцисс на две единицы масштаба вправо или сам график переносим на две единицы влево.
Параллельный перенос (сдвиг) вдоль оси ординат
График функции у=f(х+b) получаем из графика функции у=f(х) с помощью параллельного переноса (сдвига) последнего вдоль оси Оу на |b| единиц масштаба в направлении, имеющем знак числа b.
Например, для построения графика функции у=f(х)-4 вспомогательную ось абсцисс графика функции у=f(х) поднимаем вдоль оси ординат на четыре единицы или сам график переносим на 4 единицы вниз.
Растяжение или сжатие по оси абсцисс
График функции у=f(kх) получаем из графика функции у=f(х ) с помощью сжатия по оси абсцисс исходного графика пропорционально коэффициенту k при аргументе: если k>1, то график сжимается в k раз, а если 0 1, то график растягивается в m раз, если 0 22.07.2010
График функции что первое х или у
Свойства функции
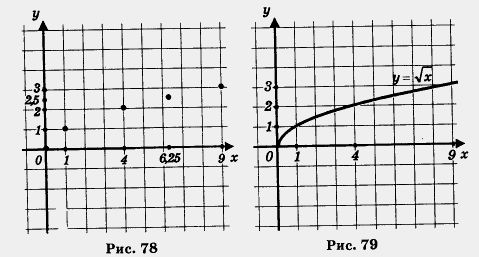
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (рис. 79).
1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; у > 0 при х > 0.
3. Функция возрастает на луче [0, + оо).
4. Функция ограничена снизу, но не ограничена сверху.
5. унаим. = 0 (достигается при х = 0), унаи6 не существует.
6. Функция непрерывна на луче [0, +оо).
Комментариев требует лишь свойство 4. Почему мы считаем, что функция не ограничена сверху? Возьмем, например, число 10. Найдется ли такое значение х, для которого будет выполнено неравенство 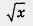
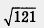
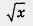
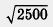
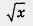
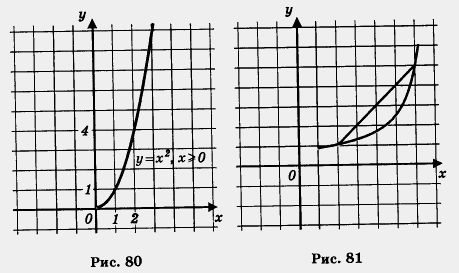
Обычно говорят, что функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 81); функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка (рис. 82).
Свойство выпуклости будем в дальнейшем включать в процедуру чтения графика.
Пример 1. Найти наименьшее и наибольшее значения функции у = 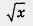
а) [0, 4]; б) [1, 5].
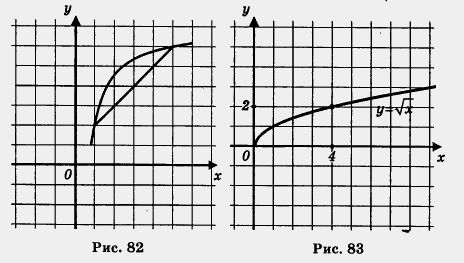
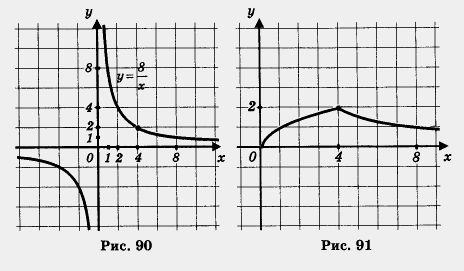
Решение, а) Построим график функции у = 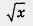
б) Построим график функции у = 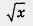
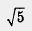
О т в е т: а) унаим. = 0; унаиб = 2; б) унаим. = 1; ушиб =
3. Функция убывает на луче [0, + оо).
4. Функция ограничена сверху и не ограничена снизу.
5 Унаиб. = 0 (достигается при х = 0), унаим не существует.
6. Функция непрерывна на луче [0, + од).
7. Область значений функции — луч (- оо, 0].
8. Функция выпукла вниз.
Пример 5. Построить и прочитать график функции y =f(x), где
Решение. Сначала построим график функции у = 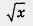
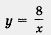
Перечислим свойства функции у — f(x), т.е. прочитаем график.
1. Область определения функции — луч [0, + °о).
2. у = 0 при x = 0; у > 0 при х > 0.
3. Функция возрастает на отрезке [0, 4] и убывает на луче [4, + оо).
4. Функция ограничена и снизу и сверху.
5 Унаим. = 0 (достигается при х = 0); унаи6 = 2 (достигается при х = 4).
6. Функция непрерывна в заданной области определения.
7. Область значений функции — отрезок [0, 2].
8. Функция выпукла вверх на отрезке [0, 4] и выпукла вниз на луче [4, + оо).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Если у вас есть исправления или предложения к данному уроку, напишите нам.