губка менгера что это
Губка Менгера
Построение
Куб 
с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба удаляются центральный куб и все прилежащие к нему по двумерным граням кубы этого подразделения. Получается множество 
, состоящее из 20 оставшихся замкнутых кубов «первого ранга». Поступая точно так же с каждым из кубов первого ранга, получим множество 
, состоящее из 400 кубов второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность
пересечение членов которой есть губка Менгера.
Свойства
См. также
Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)
Полезное
Смотреть что такое «Губка Менгера» в других словарях:
Губка Мегера — Губка Менгера геометрический фрактал, один из трёхмерных аналогов ковра Серпинского. Построение Куб K0 с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба K0 удаляются центральный куб и все прилежащие к нему по… … Википедия
Губка (значения) — В Викисловаре есть статья «губка» Губка: Губки тип беспозвоночных животных Губки для посуды изделие из губчатого материала, предназначенное для мытья посуды Губка обжимная часть слесарно монтажного инструмента, такого как… … Википедия
Кривая Менгера — Губка Менгера геометрический фрактал, один из трёхмерных аналогов ковра Серпинского. Построение Куб K0 с ребром 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из куба K0 удаляются центральный куб и все прилежащие к нему по… … Википедия
Кривая Урысона — (далее кривая) наиболее общее (но не чрезмерно) определение кривой, введённое Урысоном в 1921. Это определение обобщает определение Кантора на произвольную размерность. Определение формулируется следующим образом: Кривой называется связное… … Википедия
Индекс ветвления — Кривая Урысона (далее кривая) наиболее общее (но не чрезмерно) определение кривой, введённое Урысоном в 1921. Это определение обобщает определение Кантора на произвольную размерность. Определение формулируется следующим образом: Кривой… … Википедия
Фрактал — Множество Мандельброта классический образец фрактала … Википедия
Ковёр Серпинского — Ковёр (квадрат) Серпинского Ковёр Серпинского (квадрат Серпинского) фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вац … Википедия
Фрактальная графика — Множество Мандельброта классический образец фрактала Фрактал (лат. fractus дробленый) термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре… … Википедия
Фракталы — Множество Мандельброта классический образец фрактала Фрактал (лат. fractus дробленый) термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре… … Википедия
Кривая Коха — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия
WolframAlpha по-русски
Губка Менгера и другие трехмерные фракталы в Вольфрам Альфа
Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.
 |
| Menger sponge, губка Менгера |
Любой фрактал строится по определенному правилу, которое последовательно применяется неограниченное количество раз. Каждый такой раз называется итерацией.
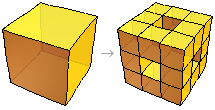
Итеративный алгоритм построения губки Менгера достаточно простой: исходный куб со стороной 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из него удаляются один центральный куб и 6 прилежащих к нему по граням кубов. Получается множество, состоящее из 20 оставшихся меньших кубов. Поступая так же с каждым из этих кубов, получим множество, состоящее уже из 400 меньших кубов. Продолжая этот процесс бесконечно, получим губку Менгера.
Губка Менгера стала широко известной, не только потому, что имеет характерную форму, которая дарит эстетическое наслаждение от ее созерцания. Динамику популярности этого трехмерного фрактала по всему миру в реальном времени показывает график Google Trands (дождитесь загрузки данных):
Кроме внешней привлекательности, губка Менгера имеет очень интересные и неожиданные свойства, о которых стоит упомянуть отдельно.
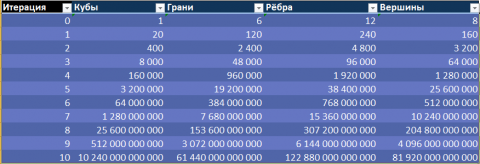
Например, если количество итераций при построении данного фрактала по указанному выше правилу, равно 0, мы получаем геометрический объект, площадь поверхности которого равна 6, а его объем равен 1 или 100% от объема исходного тела:
При количестве итераций равном 1, получим губку Менгера с площадью поверхности 8, и объемом 20/27 (примерно 0,74 или 74% от исходного объема):
Соответственно, при количестве итераций равном 2, получаем объект, показанный вначале этой статьи, с площадью поверхности 352/27 и объемом 400/729 (примерно 55% от исходного):
Если рассмотреть бесконечную последовательность значений площади поверхности и объема губки Менгера, то в пределе площадь поверхности этого фрактала стремится к бесконечности, а в его объем стремится к нулю. В этом заключается одно из самых удивительных свойств губки Менгера. При этом значение ее фрактальной размерности (capacity dimention) стремится к отношению ln(20)/ln(3):
Также Вольфрам Альфа предлагает всем, кого интересуют эксперименты с фракталами, мобильное приложение Wolfram Fractals Reference App, которое можно загрузить через iTunes или Gogle Play со станицы Fractals Reference App.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
СОДЕРЖАНИЕ
Строительство
Строение губки Менгера можно описать следующим образом:
Вторая итерация дает губку уровня 2, третья итерация дает губку уровня 3 и так далее. Сама губка Менгера является пределом этого процесса после бесконечного количества итераций.
Характеристики
Эксперименты также показали, что для одного и того же материала кубики со структурой губки Менгера могут рассеивать удары в пять раз лучше, чем кубы без пор.
Формальное определение
Формально губку Менгера можно определить так:
M знак равно ⋂ п ∈ N M п <\ Displaystyle M: = \ bigcap _ <п \ in \ mathbb 
MegaMenger
Один из мегаменжеров из Университета Бата
Модель тетрикс, просматриваемая через центр Кембриджского мегаменгера уровня 3 на Кембриджском научном фестивале 2015 года.
Подобные фракталы
Иерусалимский куб
Построение Иерусалимского куба можно описать следующим образом:
Каждая итерация добавляет восемь кубов первого ранга и двенадцать кубиков второго ранга, что в двадцать раз больше. (Подобно губке Менгера, но с двумя кубиками разного размера.) Итерация бесконечное количество раз приводит к кубу Иерусалима.
Третья итерация Иерусалимского куба
3D-печатная модель Иерусалимский куб
Снежинка Серпинского-Менгера. Сохраняются восемь угловых кубиков и один центральный куб.
СОДЕРЖАНИЕ
Строительство
Строение губки Менгера можно описать следующим образом:
Вторая итерация дает губку уровня 2, третья итерация дает губку уровня 3 и так далее. Сама губка Менгера является пределом этого процесса после бесконечного количества итераций.
Характеристики
Эксперименты также показали, что для одного и того же материала кубики со структурой губки Менгера могут рассеивать удары в пять раз лучше, чем кубы без пор.
Формальное определение
Формально губку Менгера можно определить так:
M знак равно ⋂ п ∈ N M п <\ Displaystyle M: = \ bigcap _ <п \ in \ mathbb
MegaMenger
Один из мегаменжеров из Университета Бата
Модель тетрикс, просматриваемая через центр Кембриджского мегаменгера уровня 3 на Кембриджском научном фестивале 2015 года.
Подобные фракталы
Иерусалимский куб
Построение Иерусалимского куба можно описать следующим образом:
Каждая итерация добавляет восемь кубов первого ранга и двенадцать кубиков второго ранга, что в двадцать раз больше. (Подобно губке Менгера, но с двумя кубиками разного размера.) Итерация бесконечное количество раз приводит к кубу Иерусалима.
Третья итерация Иерусалимского куба
3D-печатная модель Иерусалимский куб
Снежинка Серпинского-Менгера. Сохраняются восемь угловых кубиков и один центральный куб.
Публикации сообщества
Трёхмерные фракталы, губки и архитектура
Я хотела бы рассказать о проектно-исследовательской работе, посвящённой моделированию и исследованию свойств трёхмерных фракталов. Тема была предложена старшеклассникам для подготовки к научно-практической конференции. Важная педагогическая задача работы над проектом заключалась в изучении содержательных примеров использования математических идей и методов в различных областях окружающего мира.
К сожалению, фрактальная геометрия не входит в базовый курс школьной математики, хотя фрактальные конструкции гораздо лучше обеспечивают представление многих природных явлений, чем объекты классической евклидовой геометрии.
Почему геометрию называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. Облака – это не сферы, горы – это не конусы, линия берега – это не окружности, и кора не является гладкой, и молния распространяется по прямой… Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Число различных масштабов длин в структурах всегда бесконечно.
Работа над проектом началась со знакомства с базовыми понятиями теории фракталов.
Фрактал (от латинского fractus, означающего «сломанный, разбитый») — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
В общем случае, термин «фрактал» может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
Губка Менгера — геометрический фрактал, трёхмерный аналог ковра Серпинского.
Фрактал ковер Серпинского получается путём вырезания частей из квадрата. Возьмём квадрат, разделим его на девять квадратов, а средний вырежем. То же сделаем и с остальными, меньшими квадратами. Ковёр Серпинского имеет нулевую площадь.
Алгоритм построения губки Менгера происходит по тому же принципу, что и ковёр Серпинского. Строится губка Менгера на основе куба. Каждая грань куба, имеющая единичную длину, делится на 9 равных квадратиков так же, как и при построении квадратного ковра Серпинского. В результате исходный куб разбивается на 27 одинаковых кубиков с длиной ребра, равной 1/3. Затем, удаляя 7 кубиков (один центральный и 6 из центра каждой из граней), противоположные грани исходного куба соединяются сквозным центральным отверстием квадратной формы. В результате из 27 остается 20 маленьких кубиков. Такая итерационная процедура с вырезанием сквозных отверстий и последующего превращения каждого оставшегося кубика в 20 еще более мелких (размера в три раза меньше исходного) продолжается до бесконечности. В результате этих операций образуется самоподобный объект, называемый губкой Менгера. Губка Менгера имеет нулевой объём, но бесконечную площадь граней.
Казалось бы, фрактальные конструкции являются объектами чистой математики. Но они нашли своё материальное воплощение в архитектуре. Архитектура, начиная с фрагментов, деталей и заканчивая пространством города в целом – это система, обладающая фрактальными свойствами.
Сначала пористость была планировочной идеей, — рассказывает Холл, — как возможность связать здание с ландшафтом. Затем она стала конструктивной идеей — как сохранить конструкцию здания, вынимая из него куски железобетона. И наконец, она стала социальной идеей — эти вырванные куски, эти ниши в здании стали пространством общения для студентов, архитектура стала катализатором социального пространства.
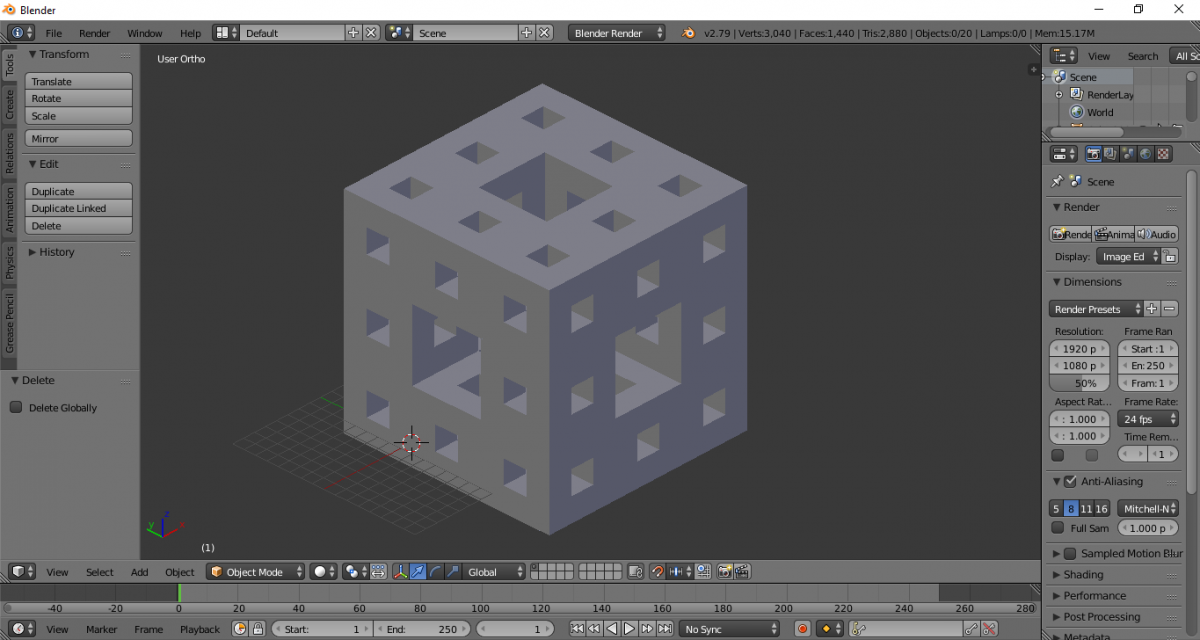
Приведу пример построения губки Менгера в Blender.
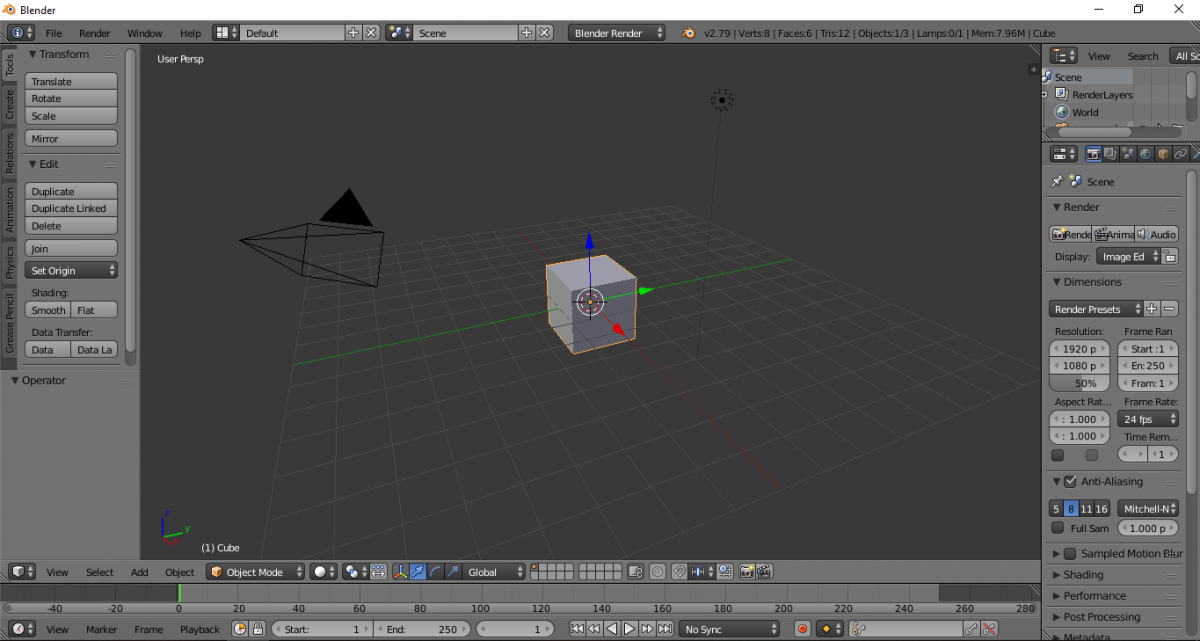
Открываем Blender. Удаляем камеру и источник освещения. Оставляем только куб.
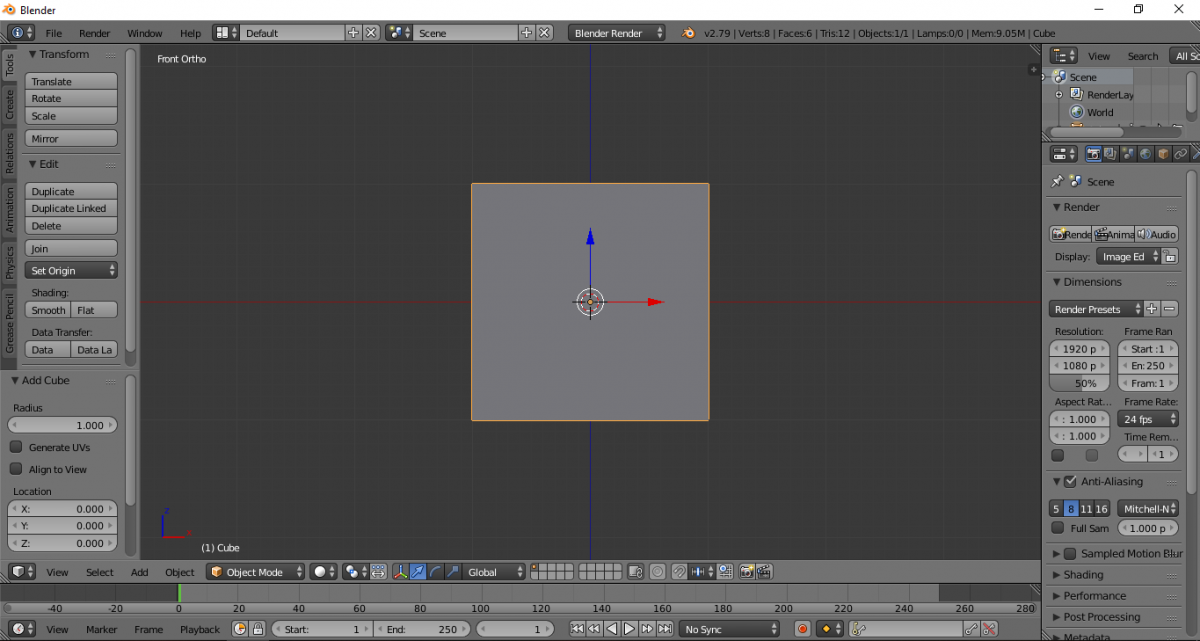
Переключаемся в ортогональную проекцию.
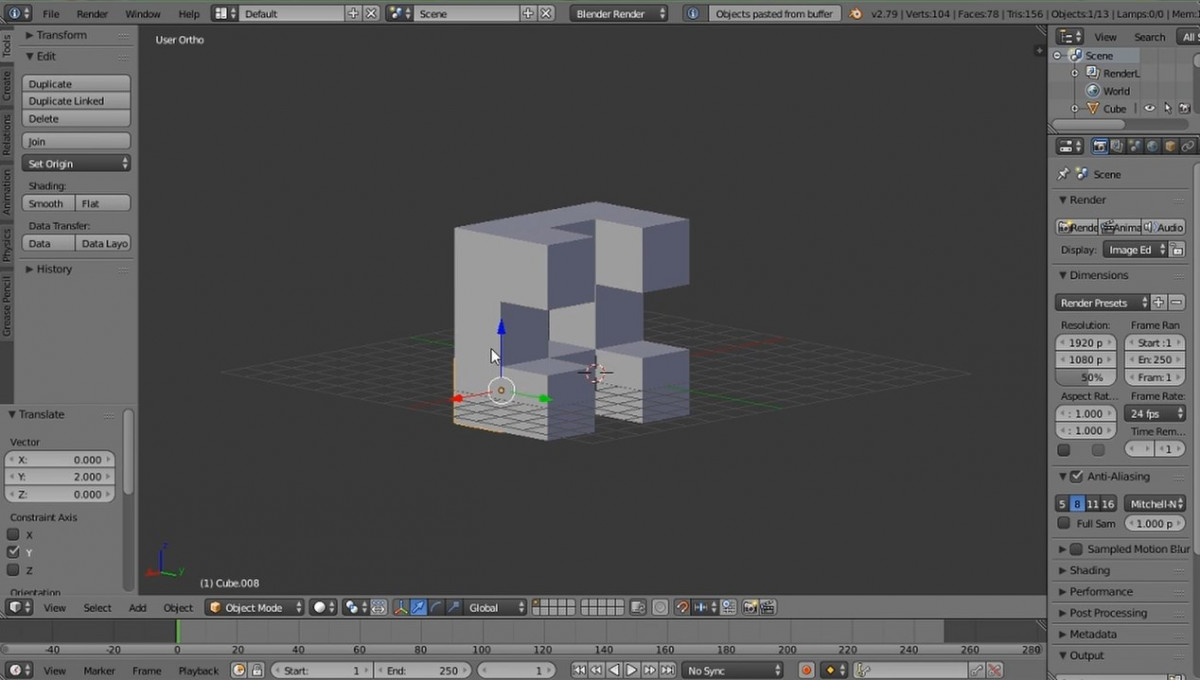
С помощью копирования кубиков создаём создаём заготовку для первой итерации губки Менгера.
Объединяем кубы (сочетание клавиш Ctrl+J).
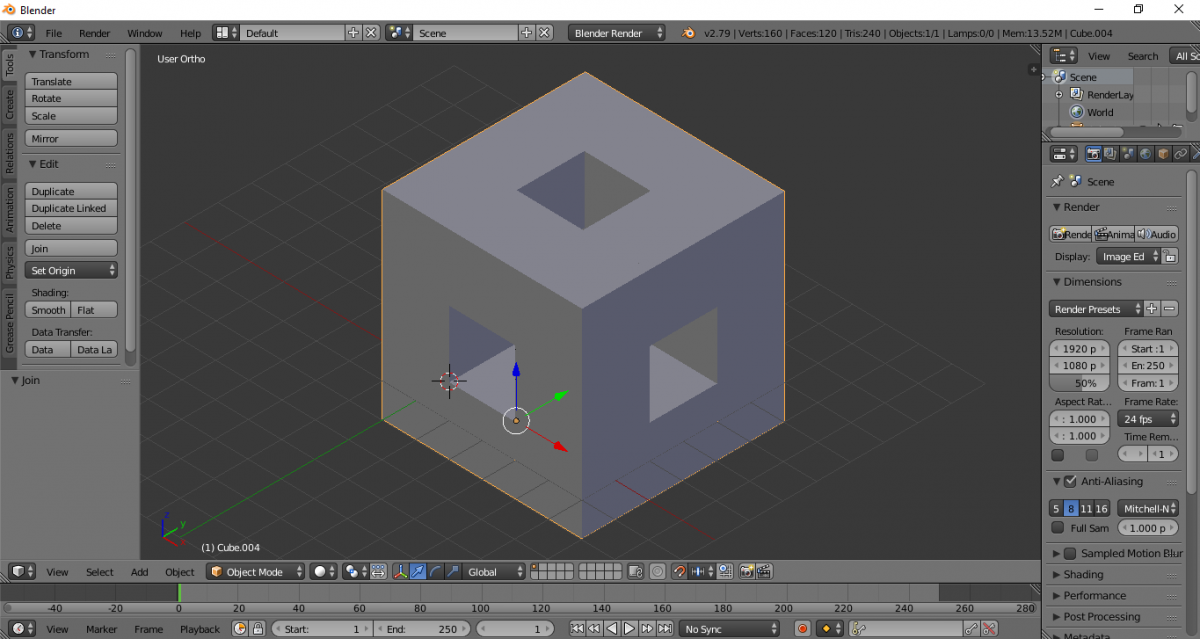
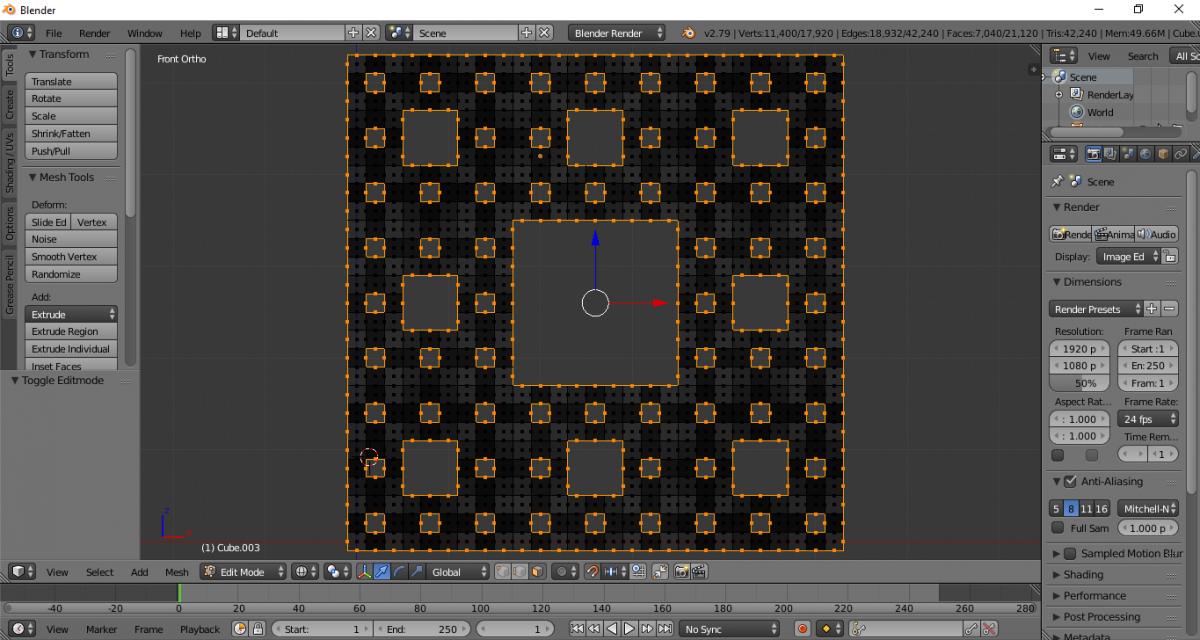
Переключаемся в ортодоксальную проекцию. Выделяем грани. В виде спереди, сбоку и сверху и скрываем их (клавиша H).
Получившуюся фигуру удаляем.
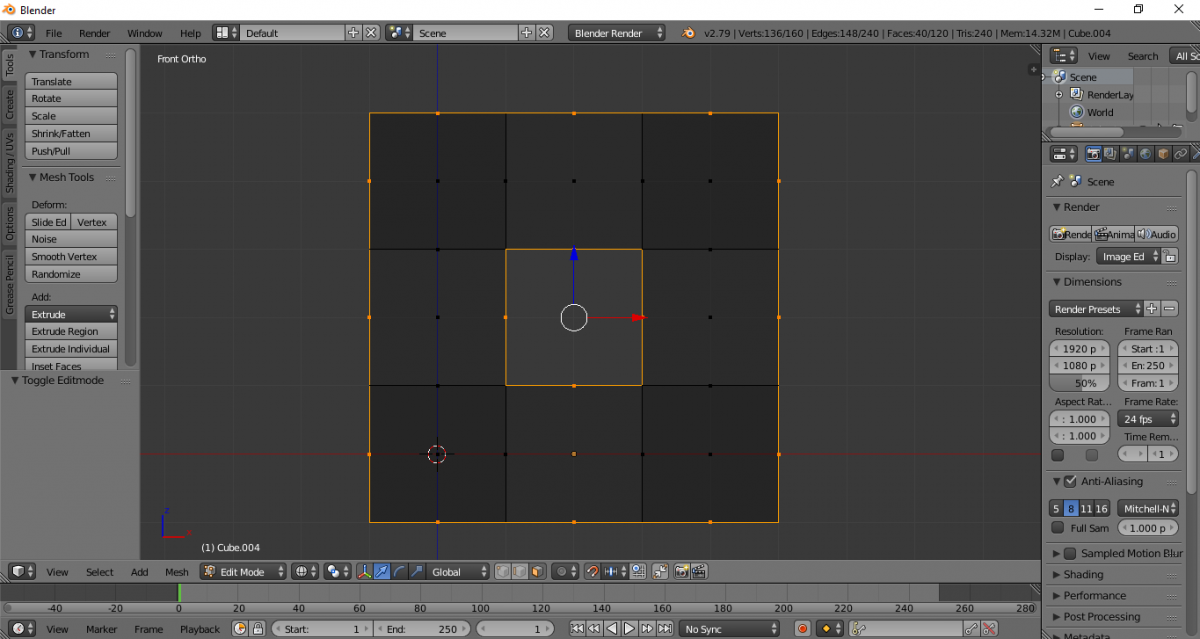
Возвращаем фигуру (сочетание клавиш Alt+H) и удаляем дубликаты. После создаем следующую фигуру, по аналогии с предыдущим шагом.
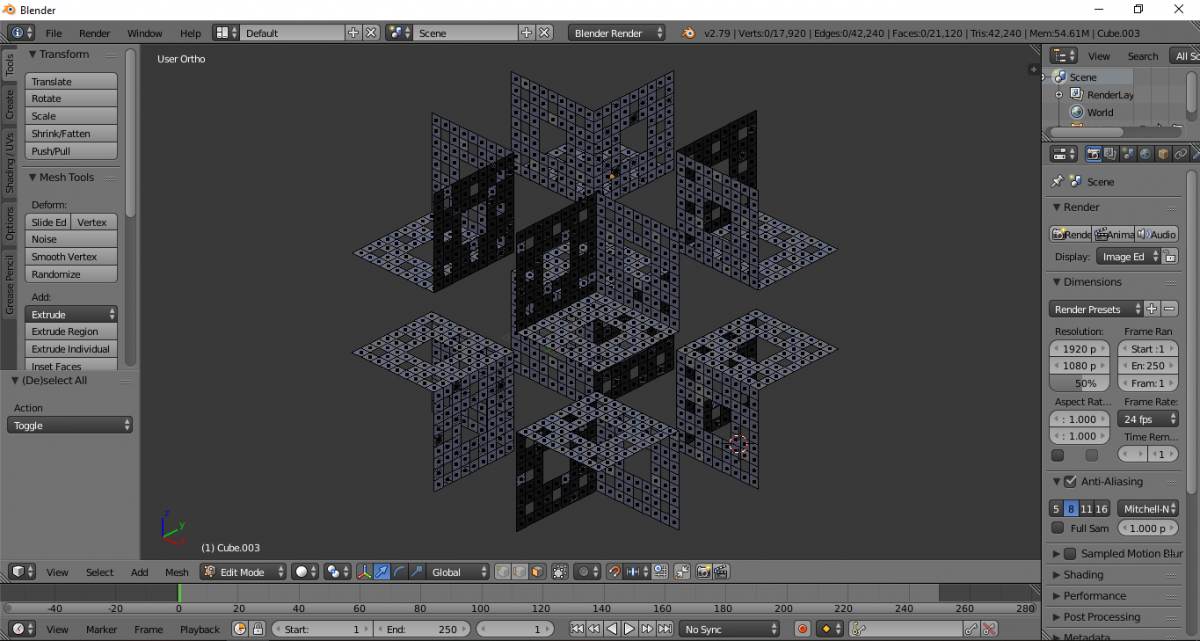
Повторяем итерацию ещё раз. Выделяем необходимые элементы.
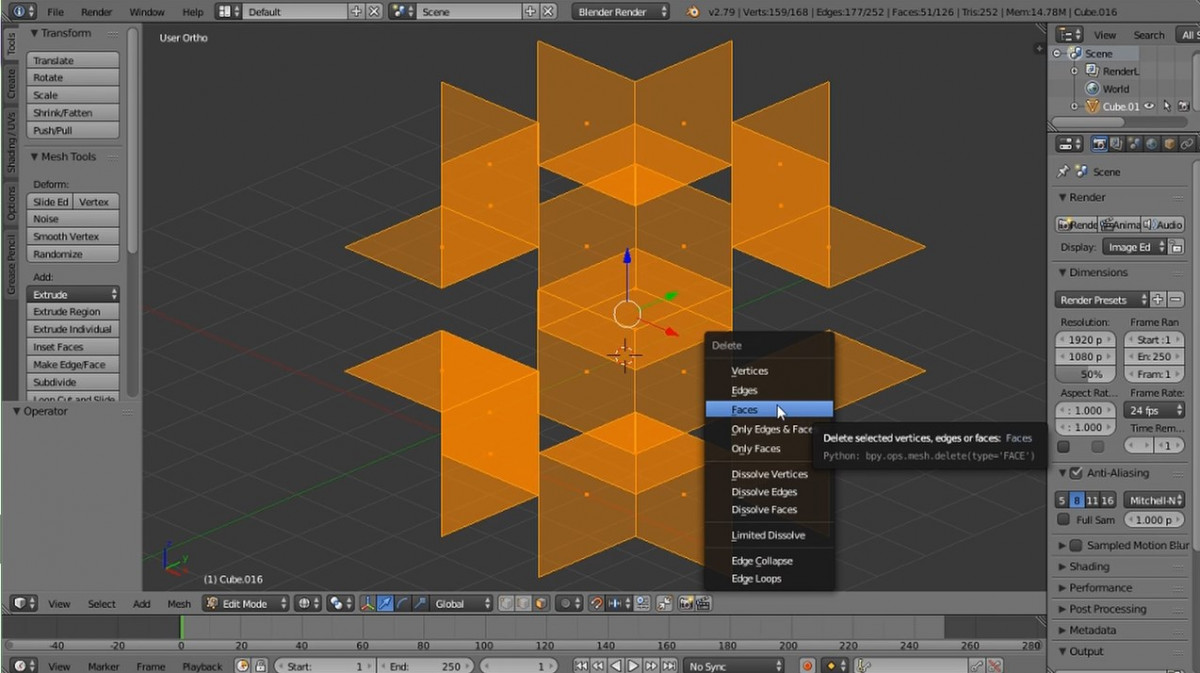
Удаляем лишние грани.
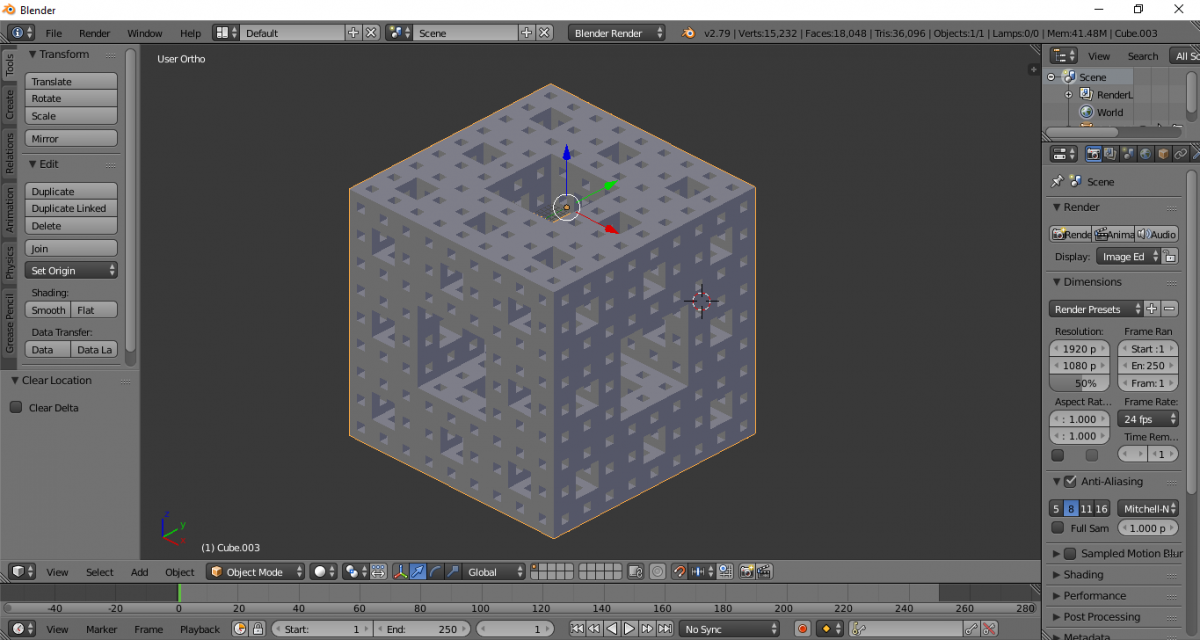
Трёхмерный фрактал губка Менгера построен.
Отмечу, что привела лишь один из возможных способов моделирования губки Менгера. Поиск других, возможно, более оптимальных способов построения, является задачей проектно-исследовательской работы. Что меня особенно порадовало и даже несколько приятно удивило, так это то, что тема вызвала интерес у учеников. Они предложили содержательные идеи для развития и доработки проекта.