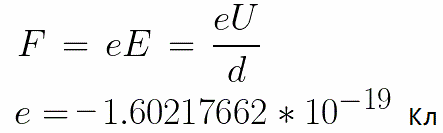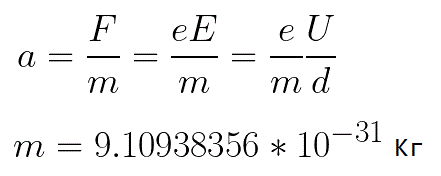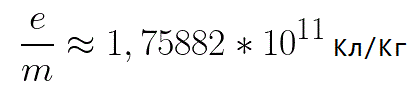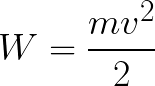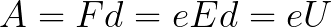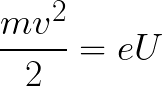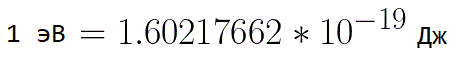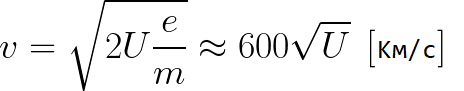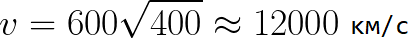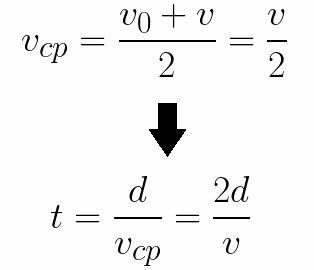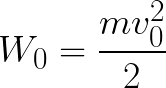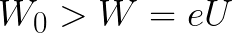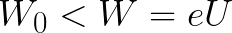кинетическая энергия электрона в магнитном поле
ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ
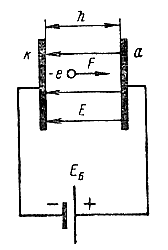
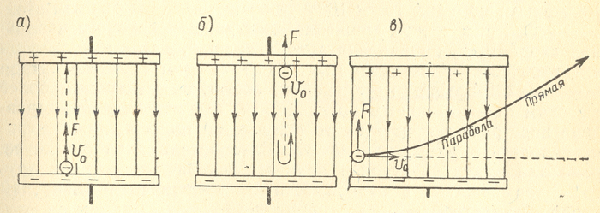
На рис.1 а, изображено электрическое поле в вакууме между двумя плоскими электродами. Они могут представлять собой катод и анод диода или любые два соседних электрода многоэлектродного прибора. Представим себе, что из электрода, имеющего более низкий потенциал, например из жатода, вылетает электрон с некоторой начальной скоростью Vo. Поле действует на электрон с силой F и ускоряет его движение к электроду, имеющему более высокий положительный потенциал, например к аноду. Иначе говоря, электрон притягивается к электроду с более высоким положительным потенциалом. Поэтому поле в данном случае называют ускоряющим. Двигаясь ускоренно, электрон приобретает наибольшую скорость в конце своего пути, т. е. при ударе об электрод, к которому он летит. В момент удара кинетическая энергия электрона также будет наибольшей. Таким образом, при движении электрона в ускоряющем поле происходит увеличение кинетической энергии электрона за счет того, что поле совершает работу по перемещению электрона. Электрон всегда отнимает энергию от ускоряющего поля.
Скорость, приобретаемая электроном при движении в ускоряющем поле, зависит исключительно от пройденной разности потенциалов U и определяется формулой
Удобно скорости электронов выражать условно в вольтах. Например, скорость электрона 10 в, означает такую скорость, которую электрон приобретает в результате движения в ускоряющем поле с разностью потенциалов 10 в. Из приведенной формулы легко найти, что при U — 100 в скорость V
6 000 км/сек. При таких больших скоростях время пролета электрона в пространстве между электродами получается весьма малым, порядка 10 в минус 8 — 10 в минус 10 сек.
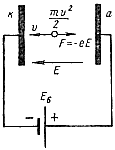
Рассмотрим теперь движение электрона, у которого начальная скорость Vo направлена против силы F, действующей на электрон со стороны поля (рис.1 б). В этом случае электрон вылетает с некоторой начальной скоростью из электрода с более высоким положительным потенциалом. Та,к как сила F направлена навстречу скорости Vo, то получается торможение электрона и поле называют тормозящим. Следовательно, одно и то же поле для одних электронов является ускоряющим, а для других— тормозящим, в зависимости от направления начальной скорости электрона.
Кинетическая энергия электрона в магнитном поле
В некоторых электронных приборах используется влияние магнитного поля на движущиеся в нем электроны.
В § 3-2, в было получено выражение (3-6) для силы, с которой однородное магнитное поле действует на электрон, движущийся перпендикулярно направлению поля. Величина этой силы пропорциональна произведению магнитной индукции В, заряда электрона 

Из выражения силы (3-6) следует, что при 

Если на электрон действует только магнитное поле, то он будет перемещаться по окружности радиуса 
Сила F является центростремительной и уравновешивается центробежной силой электрона 
Так как эти силы равны, то можно написать
откуда определяется радиус, окружности
Отношение массы электрона к его заряду постоянно, следовательно, радиус окружности пропорционален скорости движения электрона и обратно пропорционален магнитной индукции поля.
Рис. 13-4. Движение электрона в магнитном поле при начальной скорости v в плоскости, перпендикулярной вектору магнитной индукции поля.
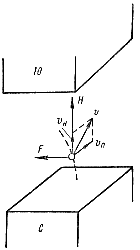
Рис. 13-5. Движение электрона в магнитном поле при начальной скорости, направленной под острым углом к вектору магнитной индукции поля.
Если начальная скорость электрона не перпендикулярна направлению поля, то ее следует разложить на две составляющие: нормальную, т. е. перпендикулярную к направлению поля 

Первая составляющая скорости 

Движение электронов в электрическом и магнитном полях
Если два плоских, параллельно расположенных электрода поместить в вакуум и подключить к источнику электродвижущей силы, то в пространстве между электродами образуется электрическое поле, силовые линии которого будут прямолинейны, параллельны друг другу и перпендикулярны к поверхностям обоих электродов.
Знак минус свидетельствует о том, что сила F, действующая на отрицательный заряд —е, и напряженность поля Е имеют противоположные направления. Для однородного электрического поля произведение напряженности Е на расстояние между электродами h равно приложенной разности потенциалов между электронами:
и U к и U а — потенциалы электродов к и а.
 |
 |
 |
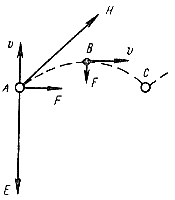 |
Дальнейшее движение электрона происходит под действием магнитного и ставшего для него тормозящим электрического поля. В точке С вся кинетическая энергия, запасенная электроном ранее, будет израсходована на преодоление тормозящего электрического поля. Потенциал точки С равен потенциалу точки А. Электрон, описав циклоидную траекторию, возвращается на прежний потенциальный уровень.
Физика. 10 класс
§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?
Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).
Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:
где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.
Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.
Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.
* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑
Электрон в электрическом поле
Движение электрона в электрическом поле является одним из важнейших для электротехники физических процессов. Разберемся как это происходит в вакууме. Сначала рассмотрим пример движения электрона от катода к аноду в однородном электрическом поле.
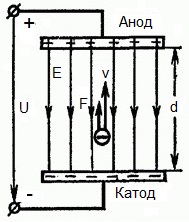
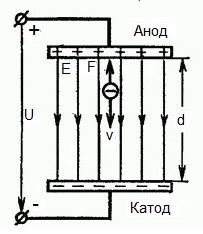
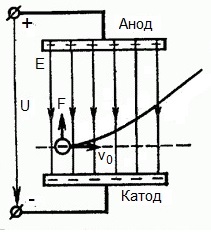
На приведенном ниже рисунке изображена ситуация, когда электрон покидает отрицательный электрод (катод) с пренебрежимо малой начальной скоростью (стремящейся к нулю), и попадает в однородное электрическое поле, присутствующее между двумя электродами.
К электродам приложено постоянное напряжение U, а электрическое поле обладает соответствующей напряженностью E. Расстояние между электродами равно d. В данном случае на электрон со стороны поля будет действовать сила F, пропорциональная заряду электрона и напряженности поля:
Поскольку электрон обладает отрицательным зарядом, то эта сила будет направлена против вектора E напряженности поля. Соответственно электрон будет в данном направлении электрическим полем ускоряться.
Ускорение a, которое испытывает электрон, пропорционально величине действующей на него силы F и обратно пропорционально массе электрона m. Поскольку поле однородно, ускорение для данной картины можно выразить так:
В этой формуле отношение заряда электрона к его массе есть удельный заряд электрона — величина, являющаяся физической константой:
Итак, электрон находится в ускоряющем электрическом поле, ибо направление начальной скорости v0 совпадает с направлением силы F со стороны поля, и электрон движется поэтому равноускоренно. Если никаких препятствий нет, то он пройдет путь d между электродами и попадет на анод (положительный электрод) с некой скоростью v. В момент когда электрон достигнет анода, его кинетическая энергия будет соответственно равна:
Поскольку на всем пути d электрон ускорялся силами электрического поля, то данную кинетическую энергию он приобрел в результате работы, которую совершила сила, действующая со стороны поля. Эта работа равна:
Тогда кинетическая энергия, которую приобрел электрон двигаясь в поле, может быть найдена следующим образом:
То есть это есть ни что иное, как работа сил поля по ускорению электрона между точками с разностью потенциалов U.
В подобных ситуациях для выражения энергии электрона удобно использовать такую единицу измерения как «электронвольт», равную энергии электрона при напряжении в 1 вольт. А поскольку заряд электрона является константой, то и 1 электронвольт — также постоянная величина:
Из предыдущей формулы можно легко определить скорость электрона в любой точке на его пути при движении в ускоряющем электрическом поле, зная лишь разность потенциалов которую он прошел ускоряясь:
Как мы видим, скорость электрона в ускоряющем поле зависит лишь от разности потенциалов U между конечной и стартовой точками его пути.
Представим, что электрон начал движение от катода с пренебрежимо малой скоростью, а напряжение между катодом и анодом равно 400 вольт. В этом случае в момент достижения анода его скорость будет равна:
Тут же легко можно определить время, за которое электрон пройдет расстояние d между электродами. При равноускоренном движении из состояния покоя средняя скорость находится как половина конечной скорости, тогда время ускоренного полета в электрическом поле будет равно:
Предположим что электрон покинул анод с какой-то начальной скоростью v и изначально стал двигаться в направлении катода. В этом случае сила F, действующая на электрон со стороны электрического поля, будет направлена против вектора электрической напряженности Е — от катода к аноду.
Она станет уменьшать начальную скорость электрона, то есть поле будет замедлять электрон. Значит электрон в данных условиях станет двигаться равномерно равнозамедленно. Ситуация описывается так: «электрон движется в тормозящем электрическом поле».
От анода электрон начал двигаться с отличной от нуля кинетической энергией, которая при торможении начинает уменьшаться, поскольку энергия теперь расходуется на преодоление силы, действующей со стороны поля навстречу электрону.
Если начальная кинетическая энергия электрона, когда он покинул анод, сразу была больше энергии, которую необходимо затратить полю на ускорение электрона при движении от катода к аноду (как в первом примере), то электрон пройдет расстояние d и в итоге все же достигнет катода несмотря на торможение.
А что если электрон влетает на скорости v0 в область действия электрического поля под прямым углом? Очевидно, сила со стороны поля в этой области направлена для электрона от катода к аноду, то есть против вектора напряженности электрического поля E.
Значит электрон теперь имеет две составляющие движения: первая — со скоростью v0 перпендикулярно полю, вторая — равноускоренно под действием силы со стороны поля, направленной к аноду.
Получается, что влетев в область действия поля, электрон движется по параболической траектории. Но вылетев за пределы области действия поля, электрон продолжит равномерное движение по инерции по прямолинейной траектории.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
- гонадотропин хорионический 1500 для чего назначают женщинам после эко
- кварцвинил или плитка на теплый пол
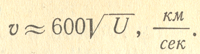




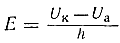
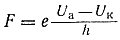 (2)
(2)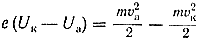
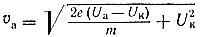 (4)
(4)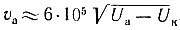 (5)
(5)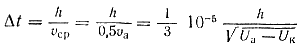 (6)
(6)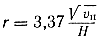 (8)
(8)