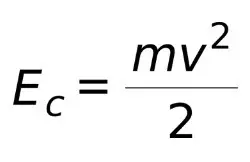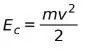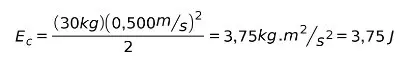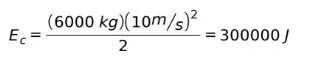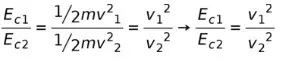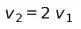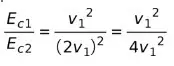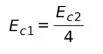кинетическая энергия тела больше чем

Тест по физике Энергия 7 класс

Тест по физике Энергия для учащихся 7 класса с ответами. Тест включает в себя 18 заданий с выбором ответа.

1. Энергия — это физическая величина, показывающая

1) как велика совершённая работа
2) как мала совершённая работа
3) каким образом совершается работа
4) какую работу может совершить тело

2. Энергия измеряется в

1) ваттах
2) джоулях
3) ньютонах
4) киловаттах

3. Энергия тела тем больше, чем

1) большее давление оно производит
2) больше его размеры
3) большую работу оно может произвести

4. Чему равно изменение энергии тела?

1) Совершённой им работе
2) Изменению действующей на него силы
3) Развиваемой им мощности
4) Среди ответов нет верного

5. Какие тела обладают потенциальной энергией?

1) Все тела, которые могут совершать работу
2) Тела, которые движутся
3) Поднятые над какой-либо поверхностью тела
4) Упругие деформированные тела

6. Какие из названных здесь тел обладают потенциальной энер­гией: комнатная люстра (№1), трамвай (№2), сосулька на крыше (№3)?

1) №1 и №2
2) №1 и №3
3) №3 и №2

7. По какой формуле можно рассчитать потенциальную энергию поднятого над землёй тела?

8. Какой из одинаковых шаров имеет наименьшую потенциальную энергию относительно поверхности пола?

9. Шары разной массы подвешены на од­ной высоте. Какой из них обладает наи­большей потенциальной энергией?

10. Какова потенциальная энергия мяча, заброшенного на крышу сарая? Масса мяча 350 г, высота сарая 3 м.

1) 105 кДж
2) 105 Дж
3) 10,5 Дж
4) 10,5 кДж

11. Какие ещё тела, кроме поднятых над землёй, могут иметь по­тенциальную энергию?

1) Никакие
2) Находящиеся на земле, но вращающиеся вокруг своей оси
3) Все сжатые тела
4) Деформированные упругие тела

12. Какие тела обладают кинетической энергией?

1) Все движущиеся тела
2) Те, которые движутся быстро
3) Медленно движущиеся тела

13. От каких величин зависит кинетическая энергия тел?

1) От времени движения
2) От объёма тела
3) От пройденного им пути
4) От массы и скорости тела

14. По какой формуле вычисляют кинетическую энергию тел?

15. Какое из названных тел обладают кинетической энергией: уличный фонарь (№1), ракета на старте (№2), дрейфующая льдина (№3), автомобили на стоянке такси (№4)?

16. Определите кинетическую энергию шара массой 0,5 кг, катя­щегося по траве со скоростью 10 м/с.

1) 5 Дж
2) 50 Дж
3) 25 Дж
4) 1000 Дж

17. Какую максимальную работу может совершить тело, обладаю­щее энергией, равной 20 Дж? 400 кДж?

1) 20 Дж; 400 кДж
2) 20 Дж; 200 кДж
3) 10 Дж; 400 кДж
4) 10 Дж; 200 кДж

18. Какими изменениями энергии сопровождаются различные физические явления?

1) Превращениями одного вида энергии в другой
2) Передачей энергии от одного тела к другому
3) Изменений энергии не происходит
4) Среди ответов нет верного

Ответы на тест по физике Энергия
1-4
2-2
3-3
4-1
5-34
6-2
7-3
8-2
9-3
10-3
11-4
12-1
13-4
14-2
15-3
16-3
17-1
18-12

Источник

Потенциальная и кинетическая энергия. Закон сохранения механической энергии

1. Камень, упав с некоторой высоты на Землю, оставляет на поверхности Земли вмятину. Во время падения он совершает работу по преодолению сопротивления воздуха, а после касания земли — работу по преодолению силы сопротивления почвы, поскольку обладает энергией. Если накачивать в закрытую пробкой банку воздух, то при некотором давлении воздуха пробка вылетит из банки, при этом воздух совершит работу по преодолению трения пробки о горло банки, благодаря тому, что воздух обладает энергией. Таким образом, тело может совершить работу, если оно обладает энергией. Энергию обозначают буквой ​ \( E \) ​. Единица работы — ​ \( [E\,] \) ​ = 1 Дж.

При совершении работы изменяется состояние тела и изменяется его энергия. Изменение энергии равно совершенной работе: ​ \( E=A \) ​.

2. Потенциальной энергией называют энергию взаимодействия тел или частей тела, зависящую от их взаимного положения.

Поскольку тела взаимодействуют с Землёй, то они обладают потенциальной энергия взаимодействия с Землёй.

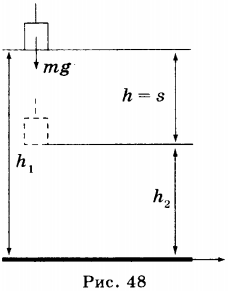
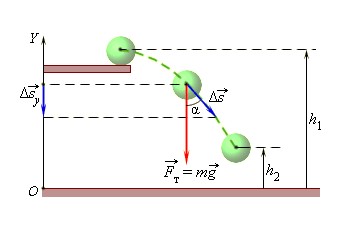
Если тело массой ​ \( m \) ​ падает с высоты ​ \( h_1 \) ​ до высоты ​ \( h_2 \) ​, то работа силы тяжести ​ \( F_т \) ​ на участке ​ \( h=h_1-h_2 \) ​ равна: ​ \( A = F_тh = mgh = mg(h_1 — h_2) \) ​ или \( A = mgh_1 — mgh_2 \) (рис. 48).

В полученной формуле ​ \( mgh_1 \) ​ характеризует начальное положение (состояние) тела, \( mgh_2 \) характеризует конечное положение (состояние) тела. Величина \( mgh_1=E_ <п1>\) — потенциальная энергия тела в начальном состоянии; величина \( mgh_2=E_ <п2>\) — потенциальная энергия тела в конечном состоянии.

Таким образом, работа силы тяжести равна изменению потенциальной энергии тела. Знак «–» означает, что при движении тела вниз и соответственно при совершении силой тяжести положительной работы потенциальная энергия тела уменьшается. Если тело поднимается вверх, то работа силы тяжести отрицательна, а потенциальная энергия тела увеличивается.

Если тело находится на некоторой высоте ​ \( h \) ​ относительно поверхности Земли, то его потенциальная энергия в данном состоянии равна ​ \( E_п=mgh \) ​. Значение потенциальной энергии зависит от того, относительно какого уровня она отсчитывается. Уровень, на котором потенциальная энергия равна нулю, называют нулевым уровнем.

В отличие от кинетической энергии потенциальной энергией обладают покоящиеся тела. Поскольку потенциальная энергия — это энергия взаимодействия, то она относится не к одному телу, а к системе взаимодействующих тел. В данном случае эту систему составляют Земля и поднятое над ней тело.

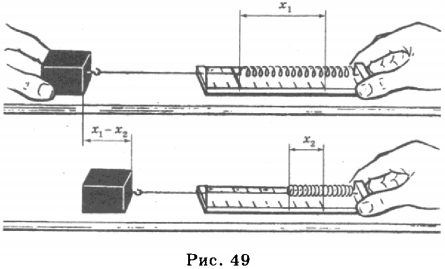
3. Потенциальной энергией обладают упруго деформированные тела. Предположим, что левый конец пружины закреплён, а к правому её концу прикреплён груз. Если пружину сжать, сместив правый её конец на ​ \( x_1 \) ​, то в пружине возникнет сила упругости ​ \( F_ <упр1>\) ​, направленная вправо (рис. 49).

Работа силы упругости равна

​ \( kx_1^2/2=E_ <п1>\) ​ — потенциальная энергия пружины в начальном состоянии, \( kx_2^2/2=E_ <п2>\) — потенциальная энергия пружины во конечном состоянии. Работа силы упругости равна изменению потенциальной энергии пружины.

Знак «–» показывает, что при растяжении и сжатии пружины сила упругости совершает отрицательную работу, потенциальная энергия пружины увеличивается, а при движении пружины к положению равновесия сила упругости совершает положительную работа, а потенциальная энергия уменьшается.

Если пружина деформирована и её витки смещены относительно положения равновесия на расстояние ​ \( x \) ​, то потенциальная энергия пружины в данном состоянии равна ​ \( E_п=kx^2/2 \) ​.

Если сила совершает положительную работу, то кинетическая энергия тела увеличивается, если работа силы отрицательная, то кинетическая энергия тела уменьшается.

Это равенство выражает закон сохранения механической энергии: полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы (силы тяготения или упругости) сохраняется.

В реальных системах действуют силы трения, которые не являются консервативными, поэтому в таких системах полная механическая энергия не сохраняется, она превращается во внутреннюю энергию.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

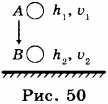
1. Два тела находятся на одной и той же высоте над поверхностью Земли. Масса одного тела ​ \( m_1 \) ​ в три раза больше массы другого тела ​ \( m_2 \) ​. Относительно поверхности Земли потенциальная энергия

1) первого тела в 3 раза больше потенциальной энергии второго тела
2) второго тела в 3 раза больше потенциальной энергии первого тела
3) первого тела в 9 раз больше потенциальной энергии второго тела
4) второго тела в 9 раз больше потенциальной энергии первого тела

2. Сравните потенциальную энергию мяча на полюсе ​ \( E_п \) ​ Земли и на широте Москвы ​ \( E_м \) ​, если он находится на одинаковой высоте относительно поверхности Земли.

1) ​ \( E_п=E_м \) ​
2) \( E_п>E_м \)
3) \( E_п
4) \( E_п\geq E_м \)

3. Тело брошено вертикально вверх. Его потенциальная энергия

1) одинакова в любые моменты движения тела
2) максимальна в момент начала движения
3) максимальна в верхней точке траектории
4) минимальна в верхней точке траектории

4. Как изменится потенциальная энергия пружины, если её удлинение уменьшить в 4 раза?

1) увеличится в 4 раза
2) увеличится в 16 раз
3) уменьшится в 4 раза
4) уменьшится в 16 раз

5. Лежащее на столе высотой 1 м яблоко массой 150 г подняли относительно стола на 10 см. Чему стала равной потенциальная энергия яблока относительно пола?

1) 0,15 Дж
2) 0,165 Дж
3) 1,5 Дж
4) 1,65 Дж

6. Скорость движущегося тела уменьшилась в 4 раза. При этом его кинетическая энергия

1) увеличилась в 16 раз
2) уменьшилась в 16 раз
3) увеличилась в 4 раза
4) уменьшилась в 4 раза

7. Два тела движутся с одинаковыми скоростями. Масса второго тела в 3 раза больше массы первого. При этом кинетическая энергия второго тела

1) больше в 9 раз
2) меньше в 9 раз
3) больше в 3 раза
4) меньше в 3 раза

8. Тело падает на пол с поверхности демонстрационного стола учителя. (Сопротивление воздуха не учитывать.) Кинетическая энергия тела

1) минимальна в момент достижения поверхности пола
2) минимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент начала движения

9. Книга, упавшая со стола на пол, обладала в момент касания пола кинетической энергией 2,4 Дж. Высота стола 1,2 м. Чему равна масса книги? Сопротивлением воздуха пренебречь.

1) 0,2 кг
2) 0,288 кг
3) 2,0 кг
4) 2,28 кг

10. С какой скоростью следует бросить тело массой 200 г с поверхности Земли вертикально вверх, чтобы его потенциальная энергия в наивысшей точке движения была равна 0,9 Дж? Сопротивлением воздуха пренебречь. Потенциальную энергию тела отсчитывать от поверхности земли.

1) 0,9 м/с
2) 3,0 м/с
3) 4,5 м/с
4) 9,0 м/с

11. Установите соответствие между физической величиной (левый столбец) и формулой, по которой она вычисляется (правый столбец). В ответе запишите подряд номера выбранных ответов

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия взаимодействия тела с Землёй
Б. Кинетическая энергия
B. Потенциальная энергия упругой деформации

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) ​ \( E=mv^2/2 \) ​
2) \( E=kx^2/2 \) ​
3) \( E=mgh \) ​

12. Мяч бросили вертикально вверх. Установите соответствие между энергией мяча (левый столбец) и характером её изменения (правый столбец) при растяжении пружины динамометра. В ответе запишите подряд номера выбранных ответов.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A. Потенциальная энергия
Б. Кинетическая энергия
B. Полная механическая энергия

ХАРАКТЕР ИЗМЕНЕНИЯ ЭНЕРГИИ
1) Уменьшается
2) Увеличивается
3) Не изменяется

Часть 2

13. Пуля массой 10 г, движущаяся со скоростью 700 м/с, пробила доску толщиной 2,5 см и при выходе из доски имела скорость 300 м/с. Определить среднюю силу сопротивления, воздействующую на пулю в доске.

Источник

Кинетическая и потенциальная энергии

Кинетическая энергия

Работа всех сил, действующих на тело, равна работе равнодействующей силы.

Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.

Определение. Кинетическая энергия

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Теорема о кинетической энергии

Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.

Теорема о кинетической энергии

Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.

Чтобы остановить тело, нужно совершить работу

Потенциальная энергия

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.

При этом сила тяжести совершила работу, равную

Определение. Потенциальная энергия

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

Потенциальная энергия пружины

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Величина E у п р = k x 2 2 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Источник

Что такое кинетическая энергия

Кинетическая энергия — это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия — это работа, которую тело выполняет, когда оно движется.

Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра — это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении.

Кинетическая энергия в физике измеряется в джоулях, сокращенно буквой J.

Формула кинетической энергии

Для расчета кинетической энергии тел используется уравнение:

Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2.

Мы можем сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя.

Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м/с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх.

Кинетическая энергия зависит от массы и скорости.

Гоночные машины спроектированы с наименьшей массой для улучшения характеристик.

Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит.

Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией.

А теперь представьте: две одинаковые машины едут, одна со скоростью 50 км/ч, а другая со скоростью 100 км/ч. Чем выше скорость, тем серьезнее авария.

Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза.

Автомобиль, движущийся со скоростью 60 км/ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км/ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии.

Как рассчитать кинетическую энергию тела?

В аэропорту хотят рассчитать кинетическую энергию 30-килограммовой упаковки в системе, которая движется со скоростью 0,500 м/с. Как мы это делаем?

Решение

Мы знаем массу и скорость упаковки, поэтому используем формулу:

Подставляя значения, имеем:

Рассуждение

Единицей кинетической энергии является джоуль, которая является той же для единицы работы. Обратите внимание, что, несмотря на то, что он тяжелый, его кинетическая энергия не так велика из-за его низкой скорости.

Ключевые моменты для запоминания

Задачи на кинетическую энергию и решение

Задача 1 на нахождение кинетической энергии

Слон в 6000 кг бежит со скоростью 10 м/с. Какова его кинетическая энергия? Какова скорость пушечного ядра весом 1 кг, если у него была та же самая кинетическая энергия слона?

Ответ

Используя уравнение кинетической энергии, энергия слона равна:

Рассчитав кинетическую энергию, мы можем получить скорость пули, очистив v:

Это означает, что скорость пули равна 775 м/с. Сравните это со скоростью слона: вот это разница!

Задача 2

Мужчина врезался в столб на своей машине. Когда он пошел, чтобы сообщить о катастрофе, он сказал, что ехал с допустимой скоростью во время аварии. Но следователь помнил физику 7 и 8 класса и установил, что скорость транспортного средства была в два раза выше, чем утверждал водитель. Какова взаимосвязь между кинетической энергией и скоростью, сообщаемой человеком, и кинетической энергией со скоростью, рассчитанной следователем?

Ответ

Мы будем рассматривать Ec1 как кинетическую энергию транспортного средства на скорости v1, сообщаемой человеком, и Ec2 как кинетическую энергию со значением скорости v2, рассчитанным исследователем. Соотношение между кинетическими энергиями рассчитывается путем деления энергий следующим образом:

Следователь сказал, что скорость во время аварии была вдвое выше, чем сообщал человек, то есть:

Подставим значение скорости в уравнение:

Исключая похожие термины, мы имеем:

Это означает, что кинетическая энергия в соответствии со скоростью, сообщаемой человеком, составляет четверть кинетической энергии по расчетам следователя. Проще говоря, ущерб, нанесенный автомобилем, был в четыре раза больше, чем сообщал мужчина.

Источник