класс эквивалентности что это такое
Граничные значения и классы эквивалентности
Одним из самых популярных вопросов на собеседовании на позицию QA Engineer является следующий: «Что такое граничные значения? Что такое классы эквивалентности?». Чаще всего эти два вопроса задают вместе, как один.
Иногда, скажем, на позицию Senior QA Engineer этот вопрос может быть даже завуалирован. Например:
— Какие практики тест-дизайна вы знаете/применяете?
— Как будете писать тест кейсы для каких-то определенных значений?
— Какие значения будете проверять?
— Как вы будете выделять граничные значения?
— В чем разница граничных значений и классов эквивалентности?
— И т.д.
Что ж, вопрос популярный, давайте разбираться.
Классы эквивалентности
Само собой, невозможно ввести все цифры, чтобы убедиться, что для каждой из них приложение будет работать правильно. Но давайте подумаем, а надо ли?
С точки зрения работы приложения между значением 500 и 600 разницы нет. Обе цифры будут умножены на соответствующий коэффициент. Следовательно, приложение будет работать одинаково в обоих случаях. Значит, эти проверки можно считать эквивалентными.
А вот еще пример. Для данного приложения целое число и дробное могут считаться эквивалентными значениями. Но только если дробное число имеет не более двух знаков после запятой: копейки и центы. Как будет обрабатываться дробное число с тремя знаками после запятой? Не важно, главное, что не так же, как целое число. И эта проверка уже эквивалентной не будет.
Суть разбиения проверок на классы эквивалентности в том, что в рамках одного класса достаточно совершить только одну проверку. Если все работает правильно, мы считаем, что для всех других эквивалентных значений все будет работать правильно.
Итак, какие проверки нам надо совершить для данного приложения?
— Проверить любое целое число или дробное с двумя знаками после запятой
— Проверить любое дробное число более чем с двумя знаками после запятой
— Проверить отрицательное число
— Проверить не числовое значение (ввести любой символ)
Граничные значения
Техника граничных значений является идейным продолжением техники эквивалентных классов. Считается, что помимо проверки значений из середины класса (например, значения 500 в нашем случае) еще надо проверять значения на границах. В нашем случае это значение 0, потому что отрицательного значения валюты быть не может.
Какой профит от этих техник?
Я довольно часто провожу собеседования начинающих инженеров в тестировании. На просьбу протестировать какое-то выдуманное приложение многие начинают действовать хаотично: вводить какие-то данные, которые придут им в голову, совершать беспорядочные манипуляции. Их действия выглядят случайными и неорганизованными.
Когда такие ребята выдыхаются и фантазия их истекает, они еще долго смотрят на листочек и пытаются что-то додумать. Они никогда не уверены, что протестировали все разумные кейсы. Вдруг случайно “придумается” еще какая-нибудь проверка поинтереснее. Знакомо? 🙂
Вышеописанные техники позволяют систематизировать проверки. Когда есть четкий план действий, полагаться на случайность не надо. Ваши действия выглядят осознанными, а вы сами понимаете, закончили проверку или нет.
Тестирование областей определения или нечто большее, чем анализ граничных значений

Все тестировщики как минимум наслышаны о таких техниках тест-дизайна, как классы эквивалентности и анализ граничных значений. Казалось бы, что может быть проще: выделить классы, взять по одному значению в каждом, проверить границы классов и значения слева и справа от границ. Но всегда ли дела обстоят настолько просто? Как быть, если после разбиения на классы оказывается, что с границами, в общем-то, проблема — их нельзя определить, поскольку данные невозможно упорядочить? Что если тестируемые параметры связаны между собой некоей логикой и зависят друг от друга? Сколько тестов достаточно? Ниже будут рассмотрены возможности двух основных техник тест-дизайна, превышающие те, что заложены в их непосредственном определении.
Область определения — математический термин — совокупность всех возможных значений переменной. Тестирование областей определения рассматривает программу как функцию многих переменных, каждая из которых принимает конечное множество значений. Каждое такое множество можно разбить как минимум на два класса эквивалентности — валидные и невалидные значения.
Классы эквивалентности
Типичные ошибки этого этапа тестирования областей определения: слишком много или слишком мало классов, классы выделены неправильно (по отношению к функциональности программы).
Выбор значений
Сочетания значений
Дефекты, зависящие от входных данных, можно поделить на те, которые возникают при конкретном значении одного параметра, и те, для возникновения которых нужно сочетание конкретных значений более чем одного параметра. Для обнаружения последних применяют комбинаторные техники тестирования, одной из которых является попарное тестирование (pairwise).
Очевидно, что при использовании сильного и/или надежного комбинирования количество тестов будет резко возрастать при увеличении количества значений какого-либо из параметров и, конечно, при увеличении количества самих параметров. Техника попарного перебора (pairwise) — один из способов уменьшить количество тестов, при этом попытавшись сохранить качество тестирования, т.е. свести к минимуму количество необнаруженных ошибок. Но применяя эту технику, важно понимать, что ошибки на стыке более чем двух значений параметров останутся ненайденными.
Другой способ уменьшить количество тестов — узнать, есть ли зависимости между входными параметрами, и учесть это в тестах. Это возможно далеко не всегда: часто тестирование черного ящика не позволяет «заглянуть внутрь». В этом случае можно попытаться выявить зависимости эмпирически и учесть их в комбинаторных тестах. Однако, есть риск ошибиться при выделении таких закономерностей.
Комбинаторные тесты можно и нужно составлять с помощью соответствующих инструментов, чтобы избежать человеческого фактора.
Искренне надеюсь, что вышеизложенное поможет вам проектировать эффективные тесты.
Немного о простом. Тест-дизайн. Часть 1
Сегодня тестирование ПО, один из ключевых процессов создания продукта. Неважно, какую Вы используете методологию, подход, процесс, тестирование ПО так или иначе всегда существует в Вашем процессе. В последние годы (да даже наверное десятилетие) тестирование ПО сформировалось в отдельную область ИТ, которая постоянно развивается в мировом сообществе.
И да, сегодня мы поговорим именно об обычных ручных (функциональных) тестировщиках, без уклона в автоматизацию, нагрузку и другие технические виды тестирования!
Сейчас профессия ручного тестировщика – это одна из самых востребованных процессий ИТ и один из самых простых способов попасть в ИТ.
Потому что тестировщики ничего не делают, им не нужны знания. Тестировать может каждый!
Потому что профессия ручного тестировщика на начальном этапе не требует специфических знаний и умений. Основное «знание» для тестировщика – это умение «разрушать» и аналитическое мышление. А главное – иметь нестандартный склад ума, находить нетривиальные решения поставленных задач. Некий монстр, умеющий крушить и ломать:)
Hard skills всегда можно научить, а вот soft skills к сожалению научить очень сложно, потому что это характер человека, его отношение к чему-либо и т.д. Обычно я косо смотрю на руководителей, которые набирают себе специалистов по ручному тестирования по hard skills. Зачем Вы это делаете. (ответы можете оставить в комментариях) Ну да ладно, продолжим:)
Если рассматривать технические особенности тестирования, которые должен знать ручной тестировщик, то их можно поделить на 2 основных части возможно многие со мной не согласятся, будут кричать как же так, ты не прав, тестирование это очень сложно – это подготовка к тестированию и выполнение тестирования.
Мы с вами рассмотрим самую интересную и увлекательную часть тестирования – подготовку к тестированию. Именно от этой части процесса тестирования зависит то, насколько качественно и правильно вы выполните само тестирования, найдете необходимые дефекты и обеспечите довольное лицо Заказчика (ну или продукт овнера) качество задачи после внедрения.
Многие из вас, кто занимался тестированием, так или иначе, занимался подготовкой к тестированию. Отличие обычно лишь в том, насколько вы этот этап процесса тестирования формализуете. Если вы занимаете исследовательским тестированием, не пишите тестовые сценарии, вам дают систему и вы сразу кидаетесь в бой, все равно, вы готовитесь к тестированию. Зачастую, на несложных проектах, тестировщик может не замечать этого, потому что этап аналитики и подготовки к тестированию проходит у вас на бессознательном уровне. Но даже если так, он все равно есть.
И в этом цикле статей поговорим об этом.
У себя на работе я часто провожу обучения для ручных тестировщиков, и сталкиваюсь с ситуациями, что вроде все слышали о техниках тест дизайна, но в работе их никто не применяет.
Первое, когда тестировщиков учат на курсах по тестированию (или самообучение по книгам и статьям), то им рассказывают, как применять техники тест-дизайна на элементарных примерах. И главная проблема такого обучения, что тестировщики не могут перенести полученные знания на свои реальные задачи. То есть использовать техники тест-дизайна в повседневной работе.
Второе, при обучении техникам тест-дизайна, данный процесс очень формализуется, что выглядит, как необходимость тестировщику в своей работе все формализовать. А обычно это никому не надо времени на это ни у кого нет.
Если говорить простыми словами, то техники тест-дизайна – это совокупность правил, позволяющих правильно определить список проверок для тестирования. И самое важное, это использовать эти правила всегда и везде 🙂 уметь на интуитивном уровне применять данные правила. Именно умение «проводить аналитику в голове» отличает хорошего тестировщика!
В моей организации, как и общепринятых стандартах и практиках, задачами тест-дизайна являются:
А начнем мы с самого простого, а именно о 2-х основных техниках тест-дизайна, про которые все слышали, и я уверен, применяли, но скорее всего на интуитивном уровне в своей работе.
Это классы эквивалентности и граничные значения.
Что же такой классы эквивалентности?
Класс эквивалентности (Equivalence class) – это набор входных (или выходных) данных ПО, которые обрабатываются программой по одному алгоритму или приводят к одному результаты.
То есть, это некое множество значений, которое вы можете подставлять в программу и получать один и тот же результат. Результатом можем быть не только конкретные значения, действия программы, но и просто область применения. Поэтому, самые простые классы эквивалентности, на которые делятся проверки, это 2 основных класса: позитивные и негативные сценарии.
Они есть всегда. Каждый тестировщик делит проверки на эти классы, но не каждый тестировщик знает, почему он это делает. Ответ – классы эквивалентности.
Далее, каждый класс эквивалентности можем разделить на дополнительные классы и т.д. до того момента, пока проверки не будут приводить к точечным и конкретным результатам тестирования.
Система скорринга рассчитывает процентную ставку по кредиту для клиента исходя из его возраста, который вводится в форму:
Позитивными сценариями будут все значения, которые приводят к получению результата, негативными сценариями – значения, результаты которых не описаны, как ожидаемый результат.
Далее мы делим класс позитивных сценариев 3 класса вводимых значений 18-24, 25-44 и 45 +
В классе негативных сценариев мы формируем значения, исходя из необходимости проверки отказов программы, поэтому мы имеем 0, 1-17, отрицательные значения, ввод символов и т.д.
Результатом данного разбиения будет значение или диапазон значений, в котором нам необходимо выполнить всего одну проверку с любым значением из диапазона данных. Могут возникнуть такие ситуации, как одно значение в диапазоне. Это тоже отдельный класс эквивалентности и тоже требует проверки.
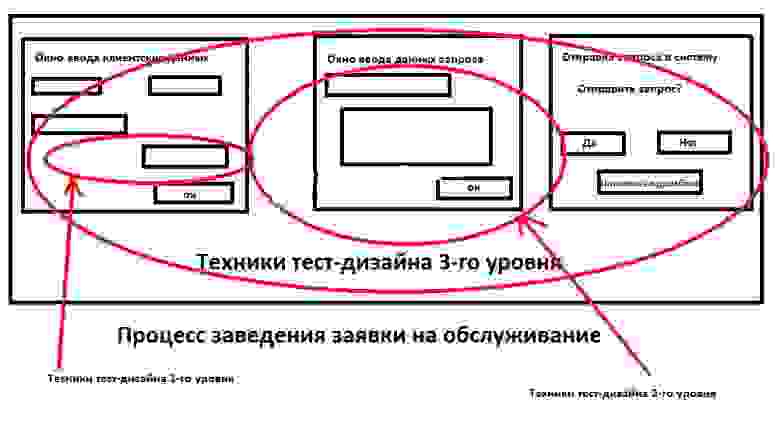
Еще одна особенность классов эквивалентности – это их применение. Я выделяю 3 уровня применения техник тест-дизайна для подготовки к тестированию.
Классы эквивалентности в большей степени относятся к 1-му уровню и применяются для проверки элементов программы. Но идеологически, данный подход можно применять и для других уровней.
Неотъемлемой часть проверки любого элемента является другая техника – граничные значения.
Граничные значения дополняют эквивалентные классы, тем самым полностью покрывая проверки элемента ПО.
Граничные значения – техника тест-дизайна, которая дополняет классы эквивалентности дополнительными проверками на границе изменения условий.
Вернемся к нашему примеру ранее.
Система скорринга рассчитывает процентную ставку по кредиту для клиента исходя из его возраста, который вводиться в форму:
Если вы подумали о длине поля на страничке Хабры, или об отпуске в теплых странах, хочу вас расстроить, это не так 🙂
Что определить граничные значения нужно нечто иное. А именно, определить, какие значения являются начальным и конечным для нашего класса. И самое важное. Годы исследований в области тестирования показали, что бОльшая часть дефектов находится тестировщиками именно на стыке значений, которые меняют условия работы программы.
Поэтому, помимо граничного значения мы используем для тестирования дополнительно 2 значения, значение перед границей и значение после границы.
Границы наших классов: 17, 18, 19, 24, 25, 26, 44, 45, 46 и max.
Далее исключаем повторяющиеся значения, и получаем значения для проверки элемента ввода данных.
-1, 0, 1, 17, 18, 19, 24, 25, 26, 44, 45, 46, max.
Значение max обычно уточняется у Заказчика или аналитика. Если не могут предоставить, то следует бросить его и не проверять необходимо подобрать значение, соответствующее здравому смыслу (вряд ли кто-то придет за кредитов в возрасте 100 лет).
Следующий шаг, это наложить граничные значения на значения классов эквивалентности, исключить лишние проверки, пользуясь правилом «достаточно одного значения для проверки одного класса» и финализировать список.
Если ранее у нас были 3 значения для 3-х классов, 19, 30 и 48, то после определения граничных значений, мы можем исключить из списка значения 30 и 48 и заменить их предграничными значениями, такими как 26 (вместо 30) и 46 (вместо 48).
Граничные значения определяются не только для числовых значений, но и для буквенных (например, границы алфавита и кодировки), даты и времени, смысловых значений. Граница числовых значений зависит от формата ввода, если у вас целые числа, например, 2, то граничные значения будут 1 и 3. Если дробные значения, то границы для числа 2 уже будут 1,9 (1,99) или 2,1 (2,01) и т.д.
Техники тест-дизайна 1-го уровня достаточно просты и понятны. Я думаю, вы скажете, да это легко, но зачем досконально проверять каждый элемент. И будете правы.
Чаще всего их применяют при разработке нового ПО, потому что единожды после проверки элементов системы при разработке они в дальнейшем не часто подлежат изменению на уровне работы элемента. Не нужно постоянно проверять каждое значение элемента в каждом экране вашей программы, но имейте ввиду, что если изменяется логика обработки данных в элементах программы, необходимо повторно убедиться в правильности обработки значений элемента.
Что ж, слишком легко. Сейчас начнем разбирать более сложные техники, готовьтесь.
Техники тест-дизайна 2-го уровня отвечают за вариативность и комбинаторику данных при проверке ПО.
Основной техникой тест-дизайна parwise testing (попарное тестирование). Суть техники заключается в минимизации вариативности комбинаций проверок, достаточных для обеспечения высокого качества ПО.
Простыми словами, в данной технике применяется правило Парето, 80 % качества можно достичь всего 20% проверок комбинаций данных.
Данная техника была выведена путем более 15-тилетнего исследования IEEE в области анализа причин возникновения дефектов в системе. Результаты исследования показали, что 98% всех дефектов возникают при конфликте ПАР входных данных или ОДНОГО входного параметра.
Почему же была выбрана пара? Погрузимся в дебри математической статистики и теории вероятности, чтобы найти ответ.
Конечно мы туда не пойдем нынче теория вероятности слишком сложна для простых ИТшников, все просто, возьмем обычную игру в кубик с 6-ю гранями.
Пусть выпадение значения 2 – это дефект, тогда вероятность появления дефекта при кидании кубика равна 1/6=0,167.
Если мы бросаем 2 кубика, то вероятность выпадения 2-х двоек (2 дефекта) становиться ниже и равна 0,167*0,167 = 0,028, для 3-х уже 0,005 и т.д.
Получается, что вероятность возникновения дефекта при комбинации 3-х и более параметров настолько мала, что ее можно отбросить.
Когда мы с вами тестируем программу, всегда есть n количество элементов, которые влияют на результат, например, форма заполнения данных по кредитной заявке. Там есть n количество полей, которые в совокупности дают результат. Именно комбинаторику данных при заполнении полей мы проверяем с помощью попарного тестирования.
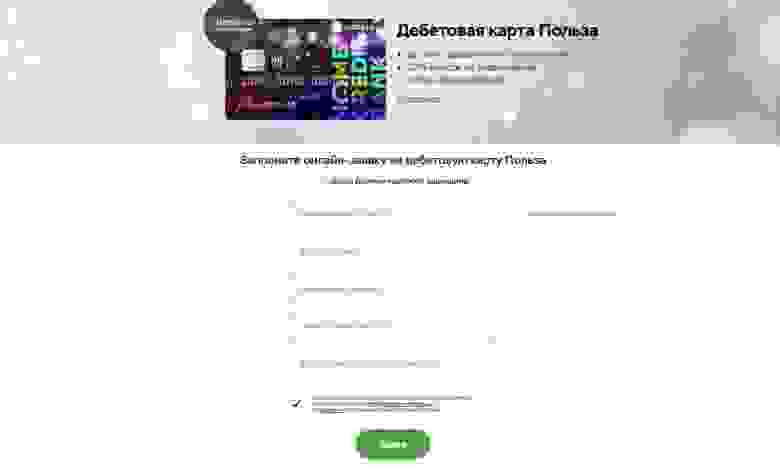
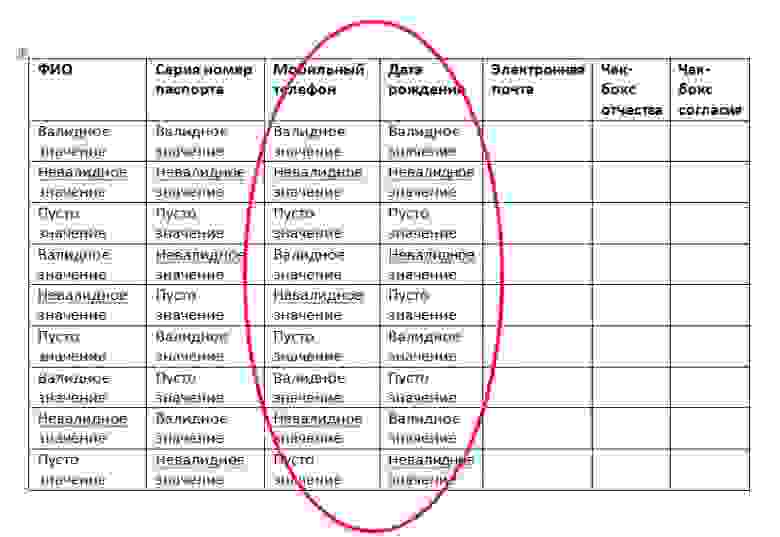
Давайте рассмотрим на примере функциональности дистанционного оформления карты в банке.
Если мы внимательно посмотрим, то увидим с Вами пять полей заполнения данных:
Очень ВАЖНО, при использовании техники попарного тестирования, мы не говорим о результате тестирования. Нам важно проверить вариативность данных при заполнении заявки.
Поле ФИО может принимать значения (классы):
Идем дальше, дата рождения, также как и мобильный телефон, серия и номер паспорта можем иметь тоже 3 состояния:
Чтобы проверить все комбинации данной формы нам бы понадобилось сделать свыше 1000 тестов, но используя попарное тестирование нам достаточно всего 9 тестов!
Магия, не думаю:)
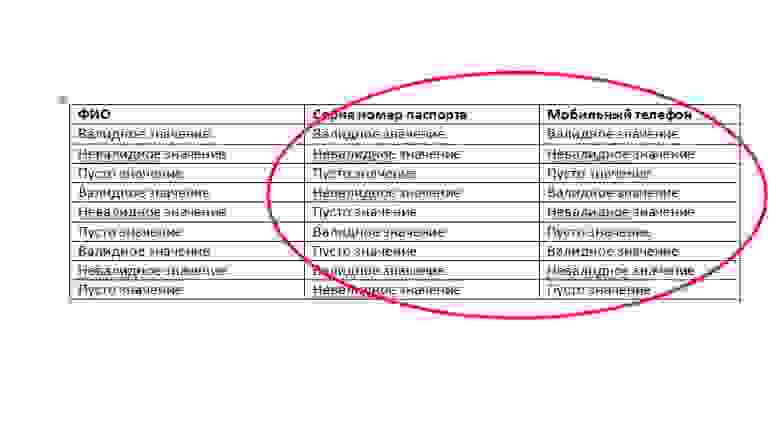
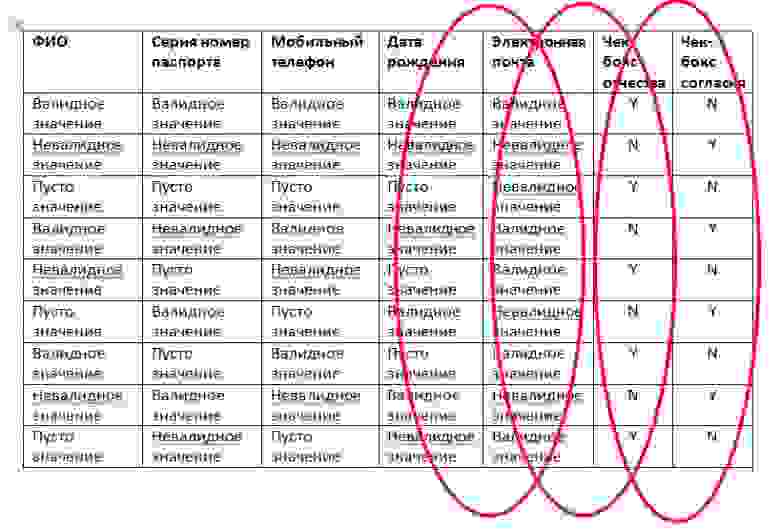
Следующий шаг – составление ортогонального массива с комбинациями данных. Самым простым способом составления массива является попарное заполнение данными, начиная с элементов, имеющих наибольшее количество значений и далее по убыванию. Так как в нашем примере есть 4 элемента с одинаковым количеством значений, то мы можем выбрать любую пару.
Мы берем ФИО и серия номер паспорта. Наша задача – перебрать все значения данной пары между собой:
После перебора одной пары, мы создаем другую пару и начинаем перебирать значения (например номер мобильного телефона)
Подключаем следующий элемент и так далее до полного заполнения всей таблицы, которая будет выглядеть так:
Таким образом мы получаем 9 тестов с конкретными классами эквивалентности, которые мы можем вводить для проверки работы вариативности данных для формы. Классы мы можем заполнять конкретными значениями, которым мы получаем с вами используя 1 уровень техник тест-дизайна.
В заключении данной статьи скажу, что рассмотренные техники тест-дизайна покрывают только часть проверок для тестирования программы, а именно проверка корректности работы элементов программы и результата их комбинаций в процессе ее работы. Во второй части мы перейдем к техникам тест-дизайна, позволяющим творить чудеса тестирования тестировать логику работы программы и процессы. Это очень важная составляющая ручного тестирования, и именно ее зачастую Вы тестируете на своей работе!
Отношения. Часть II
Формальная теория моделирования использует алгебраические отношения, включая их в сигнатуры моделей алгебраических структур, которыми описывает реальные физические, технические объекты и процессы их функционирования. Эта публикация является продолжением предшествующей, прочтение которой желательно, так как многие понятия и термины, используемые здесь, описываются там.
Предлагается изложение не в традиционном (стрелочном) стиле, а так, как мне самому пришлось всю эту кухню представлять и осваивать и по учебникам/пособиям, и по журнальным статьям. Особенно полезной вещью считаю созданный мной каталог, он позволяет выделить практически любое пространство и представить его элементы в удобном виде: матрицей, графом и др. Сразу видишь с чем имеешь дело и свойства (они уже выписаны) проверять часто не требуется.
Понятие отношения
Думаю, что термин отношение знаком каждому читателю, но просьба дать определение поставит большинство в тупик. Причин для этого много. Они чаще всего в преподавателях, которые, если и использовали отношения в процессе преподавания, внимания на этом термине не заостряли, запоминающихся примеров не приводили. Некоторые комментаторы статьи отнесли замечания на свой счет и насыпали минусов. Но шила в мешке не утаишь. Серьезных публикаций как не было, так и нет. Задайте себе вопрос, работали ли Вы с каким-либо пространством отношений? И честно себе ответьте. Что об этом пространстве можете миру поведать, для начала хотя-бы перечислить его элементы и указать свойства. Даже на СУБД Вы смотрите глазами их создателей, а они ведь тоже не все видят, или не все показывают, как, например, в микросхемах.
Здесь сделаю небольшой повтор. Начинать следует с абстрактного множества А =
А×А=<(a1, a1),(a1, а2),(a1, a3),(a2, а1),(a2, a2),(a2, a3),(a3, a1),(a3, a2),(a3, a3)>.
Получили 9 упорядоченных пар элементов из А×А, в паре первый элемент из первого сомножителя, второй — из второго. Теперь попробуем получить все подмножества из декартова квадрата А×А. Подмножества будут содержать разное количество пар: одну, две, три и так до всех 9 пар, включаем в этот список и пустое множество ∅. Сколько же получилось подмножеств? Много, а именно 2 9 = 512 элементов.
Отношения можно задавать в разном представлении:
Пространства бинарных отношений
Пространством бинарных отношений с множеством-носителем называется произвольное подмножество множества бинарных отношений заданных на. Рассмотрим основные пространства для отношений предпочтений (рис. 2.15).
Рисунок 2.15 Схема пространств бинарных отношений
Выявленные связи между пространствами используются для переноса задач принятия решений (ЗПР) из одних пространств в другие, где они могут быть решены более простым путем, а затем полученное решение возвращают в исходное пространство, где была сформулирована ЗПР.
Эти отношения представлены диаграммой на рис. 2.14. Пространства бинарных отношений (типы отношений) представлены рис. 2.15.
Отношения эквивалентности
Определение. Бинарное отношение σ ⊆ А×А, обладающее тремя свойствами рефлексивности, симметричности, транзитивности, называется, бинарным отношением эквивалентности (БОЭ). Обозначается отношение эквивалентности σ(х, у), (х, у)∊σ, хσу, х≈у. Удобно использовать матричное (табличное) представление отношения. Ниже на рис 2.24 приведено как раз матричное представление. Над множеством из 4-х элементов существует 15 БОЭ, которые все изображены.
Представление и анализ структуры отношений эквивалентности (n = 4)
Эквивалентность из бинарных отношений, пожалуй, самое распространенное БО. Редкая наука обходится без этого понятия, но даже тогда, когда эквивалентности используются в изложении каких-либо вопросов, бывает трудно понять, что в виду имел автор. Даже при корректном определении и перечислении свойств, присущих этому бинарному отношению – трудности восприятия остаются.
Начнем с примера об эквивалентностях, который иллюстрирует ограниченность их количества.
Пример 1. Пусть имеется три кубика. Составим список свойств, которыми наделены кубики и практическое использование которых (свойств кубиков) делает их как бы взаимозаменяемыми. Кубикам присвоим номера, а их свойства представим таблицей 1.
По каждому из свойств возникает БОЭ и классы эквивалентности. Продолжая список свойств, мы новых отношений эквивалентности не получим. Будут только повторы уже построенных, но для других признаков. Покажем связь БОЭ с множествами.
Рассмотрим множество из трех элементов А = <1,2,3>и получим для него все возможные разбиения на все части. ①1|2|3; ②12|3; ③13|2; ④ 1|23; ⑤123. Последнее разбиения на одну часть. Номера разбиений и БО в кружках.
Определение. Разбиением множества А называют семейство Аi, i = 1(1)I, непустых попарно непересекающихся подмножеств из А, объединение которых образует все исходное множество А=UАi, Аi∩Аj =∅, ∀ i ≠ j. Под-множества Аi называют классами эквивалентности разбиения исходного множества.
Это все разбиения множества (5 штук). Анализ БО показывает, что различных отношений эквивалентности тоже только 5 штук. Случайно ли это совпадение? Мы можем каждому разбиению сопоставить матрицу из девяти ячеек (3×3 = 9), в каждой из которых либо размещается упорядоченная пара элементов из множества А, либо ячейка остается пустой, если для соответствующей пары нет объекта. Строки и столбцы матрицы размечаются элементами множества А, а пересечению строка – столбец соответствует упорядоченная пара (i, j). В ячейку матрицы вписывается не пара, а просто единица или нуль, впрочем, нуль часто не пишут совсем.
Нет, совпадение не случайное. Оказывается, каждому разбиению множества взаимно однозначно соответствует БОЭ, при этом мощность множества может быть любой |A| = n.
Это отношение едва ли не самое частое по использованию в научном обороте, но совокупность свойств, реализуемых в этом отношении, сильно ограничивает его распространенность.
Так среди всех абстрактных бинарных отношений над множеством из трех элементов (всего их 2 9 = 512 отношений) только пять являются эквивалентностями — носителями требуемых свойств, менее одного процента.
Для |A| = 4 отношений существует 2 16 = 65536, но эквивалентностей лишь 15 штук. Это весьма редкий тип отношений. С другой стороны, отношения эквивалентности широко распространены в прикладных задачах. Везде, где имеются и рассматриваются множества самых различных объектов и различные разбиения таких множеств (не чисел) на части возникают отношения эквивалентности. Их можно назвать математическими (алгебраическими) моделями таких разбиений, классифицирующими множества объектов по различным признакам.
Решетка Р(4): все разбиения множества А =
Минимальному разбиению соответствует отношение эквивалентности П15, которое называется равенством или единичным отношением. В каждом классе эквивалентности — единственный элемент. Разбиению множества А, включающему лишь само множество А, соответствует отношение эквивалентности, содержащее все элементы декартова квадрата А×А.
Ближайший тип к отношениям эквивалентности – отношения толерантности. Множество отношений толерантности содержит в себе все отношения эквивалентности. Для носителя А из трех элементов толерантностей 8. Все они обладают свойствами рефлексивности и симметричности.
При выполнении свойства транзитивности пять из восьми толерантностей преобразует в эквивалентности (рис. 2.24 и 2.25).
Определение. Совокупность классов [a]σ эквивалентности элементов множества А называется фактор-множеством (обозначается А/σ) множества А по эквивалентности σ.
Определение. Естественным (каноническим) отображением f: A→ А/σ называется такое отображение f, при котором f(а) = [a]σ.
Отношения толерантности и их анализ
Об этих БО ранее уже упоминалось, а здесь рассмотрим их подробнее. Всем известны понятия сходство, похожесть, одинаковость, неразличимость, взаимозаменяемость объектов. Они кажутся близкими по содержанию, но при этом не одно и то же. Когда для объектов указано только сходство, то невозможно разбить их на четкие классы так, что внутри класса объекты похожи, а между объектами разных классов сходства нет. В случае сходства возникает размытая ситуация без четких границ. С другой стороны, накапливание несущественных различий у сходных объектов может привести к совершенно непохожим объектам.
В предыдущей части мы обсудили содержательный смысл отношения одинаковости (эквивалентности) объектов. Не менее важной является ситуация, когда приходится устанавливать сходство объектов.
Пусть изучается форма геометрических тел. Если одинаковость формы объектов, например, кубиков, означает их полную взаимозаменяемость в определенной ситуации обучения, то сходство – это частичная взаимозаменяемость, (когда среди кубиков встречаются очень похожие на них параллелепипеды) т. е. возможность взаимной замены с некоторыми (допустимыми в данной ситуации) потерями.
Наибольшая мера для сходства – неразличимость, а вовсе не одинаковость, как может показаться на первый взгляд. Одинаковость – свойство качественно иное. Одинаковость можно рассматривать только как частный случай неразличимости и сходства.
Все дело в том, что неразличимые объекты (так же, как и сходные, похожие) не удается разбить на классы так, чтобы в каждом классе элементы не различались, а элементы разных классов заведомо различались.
В самом деле, будем рассматривать множество точек (х, у) на плоскости. Пусть величина d имеет значение меньшее порога разрешимости глаза, т. е. d – такое расстояние, при котором две точки, находящиеся на этом расстоянии, сливаются в одну, т.е. визуально неразличимы (при выбранном удалении плоскости от наблюдателя). Рассмотрим теперь n точек, лежащих на одной прямой и отстоящих (каждая от соседних) на расстоянии d. Каждая пара
соседних точек неразличима, но, если n достаточно велико, первая и последняя точки будут отстоять друг от друга на большое расстояние и заведомо будут различимы.
Традиционный подход к изучению сходства или неразличимости состоит в том, чтобы сначала определить меру сходства, а затем исследовать взаимное расположение сходных объектов. Английский математик Зиман, изучая модели зрительного аппарата, предложил аксиоматическое определение сходства. Тем самым свойства сходства стало возможным изучать независимо от того, как конкретно оно задано в той или иной ситуации: расстоянием между объектами, совпадением каких-то признаков или субъективным мнением наблюдателя.
Введем экспликацию понятия сходства или неразличимости.
Определение. Отношение Т на множестве M называется отношением толерантности или толерантностью, если оно рефлексивно и симметрично.
Корректность такого определения видна из того, что объект заведомо неразличим сам с собой и, конечно, похож на себя (это задает рефлексивность отношения). Порядок рассмотрения двух объектов не влияет на окончательный вывод об их сходстве или несходстве (симметричность).
Из примера со зрительной неразличимостью точек плоскости видим, что транзитивность толерантности выполняется не для всех пар объектов.
Ясно также, что поскольку одинаковость есть частный случай сходства, то эквивалентность должна быть частным случаем толерантности. Сравнивая определения эквивалентности и толерантности, убеждаемся, что так оно и есть. Философский принцип: «частное богаче общего» наглядно подтверждается. Дополнительное свойство – транзитивности делает часть отношений толерантности эквивалентностями. Двое близнецов бывают настолько одинаковыми, что без риска могут сдавать экзамены друг за друга. Однако если два студента только похожи, то такая проделка, хотя и осуществима, но рискованна.
Каждый элемент множества несет определенную информацию о похожих на него элементах. Но не всю информацию, как в случае одинаковых элементов. Здесь возможны разные степени информации, которую один элемент содержит относительно другого.
Рассмотрим примеры, где толерантность задается разными способами.
Пример 2. Множество M состоит из четырехбуквенных русских слов — нарицательных существительных в именительном падеже. Будем называть такие слова сходными, если они отличаются не более чем на одну букву. Известная задача «Превращение мухи в слона» в точных терминах формулируется так. Найти последовательность слов, начинающуюся словом «муха» и кончающуюся словом «слон», любые два соседних слова в которой сходны в смысле только что данного определения. Решение этой задачи:
муха — мура — тура — тара — кара — каре — кафе — кафр — каюр — каюк — крюк — крок — срок — сток — стон — слон.
Толерантность подмножеств (граней) означает наличие у них общих вершин.
Определение. Множество M с заданным на нем отношением толерантности τ называется пространством толерантности. Таким образом, пространство толерантности есть пара (M, τ).
Пример 4. Пространство толерантности Sp допускает обобщение на бесконечный случай. Пусть H — произвольное множество. Если SH – совокупность всех непустых подмножеств множества H, то отношение толерантности Т на SH задается условием: X Т Y, если X∩Y ≠ ∅. Симметричность и рефлексивность этого отношения очевидны. Пространство SH обозначается и называется «универсальным» пространством толерантности.
Пример 6. Рассмотрим пространство толерантности, компоненты которого принимают любые действительные значения.
В частности, это множество всех точек x = (a1, a2) декартовой плоскости. Толерантность двух точек означает совпадение у них хотя бы одной координаты. Значит, две толерантные точки находятся либо на общей вертикали, либо на общей горизонтали.
Отношения частичного порядка и их анализ
Упорядоченные множества – это множества с введенным на нем отношением порядка. Определение. Множество А и бинарное отношение порядка R на нем (≤) называется частично упорядоченным, если для отношения выполнены (как и в БОЭ) три условия (одно условие другое):
Элемент х∊А ЧУМ А покрывает элемент у∊А, если х > y и не существует z∊А такого, что х > z > y. Пара элементов х, у∊А называется сравнимой, если х ≥ у или х ≤ у.
Если в ЧУМ А всякая пара его элементов является сравнимой, то А называют линейно упорядоченным множеством или цепью.
Если же некоторое ЧУМ В состоит лишь из несравнимых друг с другом элементов, то множество В называют антицепью. Цепь в ЧУМ А называется насыщенной, если она не может быть вложена ни в какую другую цепь, отличную от себя.
Аналогично определяется насыщенная антицепь. Максимальной цепью (антицепью) называется цепь (антицепь), содержащая максимальное количество элементов.
Элемент m ЧУМ А называется минимальным, если в А нет элемента х∊А, отличного от m и такого, что х≤m. Элемент M ЧУМ А называется максимальным, если в А нет элемента х «большего», чем M, отличного от M и такого, что х ≥ M.
Элемент у∊А ЧУМ А называется наибольшим, если ∀ х∊ А х ≤ у. Элемент у∊ А ЧУМ А называется наименьшим, если ∀ х∊А х ≥ у. Для наибольшего и наименьшего элементов принято использовать обозначения 1 и 0 соответственно. Их называют универсальными границами. Всякое ЧУМ А имеет не более одного наименьшего и не более одного наибольшего элементов. В ЧУМ А допустимо несколько минимальных и несколько максимальных элементов
Изображать конечное ЧУМ А удобно диаграммой Хассе, которая представляет собой ориентированный граф, его вершины распределены по уровням диаграммы и соответствуют элементам из А, а каждая дуга направляется вниз и рисуется тогда и только тогда, когда элемент х∊А покрывает элемент у∊А.
Транзитивные дуги не изображаются. Уровни диаграммы Хассе содержат элементы одинакового ранга, т.е. связанные с минимальными элементами ЧУМ путями равной длины (по числу дуг).
Пусть В непустое подмножество ЧУМ А, тогда элемент х∊А называется точной верхней гранью (обозначается supAB) множества В, если х ≥ у для всех у∊В и, если из истинности соотношения z ≥ у для всех у∊В вытекает, что z ≥ х.
Точной нижней гранью (обозначается infAB) множества В называется элемент х∊А, если х ≤ у для всех у∊В и, если из условия z ≤ у для всех у∊ В вытекает, что z ≤ х.
Пример 7. Заданы два конечных числовых множества
А = <0,1,2,…,21>и B = <6,7,10,11>.
ЧУМ (А, ≤) представлено рис. 2.26.
Совокупность В Δ всех верхних граней для В называется верхним конусом для множества В. Совокупность В ∇ всех нижних граней для В называется нижним конусом для В.
Всякое подмножество ЧУМ также является ЧУМ относительно наследованного порядка. Если в множестве существуют наибольший и/или наименьший элементы, то они являются максимальным (минимальным соответственно). Обратное неверно. Булеан обладает единственным наименьшим (Ø) и единственным наибольшим элементами.
В приведенном множестве наименьший элемент нуль (0) и он совпадает с единственным минимальным элементом, а наибольшего элемента не существует. Максимальными элементами являются <19, 20, 21>. Точная верхняя грань для B = <6,7,10,11>есть элемент 21 (это наименьший элемент в верхнем конусе).
Общая ситуация. Пусть задано множество, мощность которого*******. Из всех бинарных отношений, возможных на этом множестве, выделим бинарные отношения предпочтения и связанные с ними отношения строгих частичных порядков.
Частичные порядки отличаются от строгих частичных порядков только тем, что содержат в своем составе дополнительные элементы (в матричном представлении – диагональные) (аi, ai ) = 1, i = 1(1)n, а число тех и других порядков в полном множестве отношений одинаково. До настоящего времени не найдены зависимости (формула, алгоритм), которые позволяли бы подсчитывать и перечислять при любом n число частичных порядков.
Разными авторами непосредственным подсчетом определены и опубликованы следующие результаты (табл. 2.12).
Вычислительные эксперименты автора позволили получить не только число, но и вид (представление) частичных порядков при разных мощностях множителя-носителя отношений. Принтер задыхался печатая такие огромные списки, но не только красота требует жертв, наука тоже не отказывается от них.
В таблице 2.12 показаны: n = |A| – мощность множества-носителя; вторая строка – количество всех бинарных отношений на множестве А; и далее
|Ин(n)| – количество классов неизоморфных отношений;
|Г(n)| – количество отношений частичного порядка;
|Гн(n)| – количество классов неизоморфны отношений частичного порядка;
|Гл(n)| = n! – количество отношений линейного порядка.
Как видим, в таблице для небольших n, например, Г(n=4) имеется всего 219, приводятся данные, значения которых с увеличением n очень быстро растут, что существенно усложняет их количественный (и качественный) непосредственный анализ даже с помощью ЭВМ.
Таблица ниже иллюстрирует возможность порождения Г(n=4) всех частичных порядков из пересечения каждого с каждым линейных частичных порядков. Но в этой ситуации возникают избыточные (повторяющиеся), которые при малых n можно отсечь вручную (пересчитать). Получаются 300 матриц, но ЧУМ среди них лишь 219. Общие формулы так и не были получены. На мировом уровне ситуация аналогичная, хотя мне не довелось видеть публикаций о перечислениях ЧУМ западных авторов. Наши алгоритмы вполне оригинальны и пионерские.
Приведу возможную схему решения задачи перечисления элементов пространства частичных порядков (n=4).
Множество строгих частичных порядков при лексикографическом упорядочении линейных порядков (n=4) порождается при их взаимном пересечении.
Несколько важных определений математики, для встречающихся часто в текстах понятий.
Определение. Замкнутый интервал – это множество вида