почему в поле нет делителей нуля

в) Если b ≠ 0, d ≠ 0, то ;

г) Если b ≠ 0, с ≠ 0, d ≠ 0, то .

Источник

Геометрия и алгебра (теория колец и полей)

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Правила и принципы форума «Высшая математика»	28.10.2009 15:17
	Открыта свободная публикация вакансий для математиков	26.09.2019 16:34
	Премия для молодых математиков Образовательного фонда «Талант и успех»	21.06.2021 00:48

Конечно, поле не может иметь делителей нуля, но не всякое коммутативное ассоциативное кольцо с единицей без делителей нуля является полем. В качестве примера можно взять кольцо целых чисел (в нем нет обратимых элементов, кроме единицы).

Редактировалось 1 раз(а). Последний 04.12.2011 20:15.

Возможно я действительно понял что то не так. Вот сама теорема и доказательство необходимости.

Достаточность предлагается доказать самостоятельно. В процессе множественных попыток все доказательства сводились к тому что необходимо доказать принадлежность обратного элемента к этому кольцу.

Источник

Ч1.Вопрос20. Поле. Следствия из аксиом. Отсутствие делителей нуля. Характеристика поля; ее простота. Подполя и расширения полей. Изоморфизм колец (полей).

Опр: Полем называется множество P в котором определены операции + * (замкнуты) и выполняются следующие аксиомы:

1) Р – не нулевое кольцо.

2) Умножение коммутативно ab=ba, a,b прин Р.

3) Множество Р с исключенным нулем есть группа по умножению.

Примеры: Множество рациональных чисел, действительных, комплексных. C\R – не является полем. P= <0>– не явл.

Опр: Пусть задано поле Р; подмножество Р’ – которое само явл-ся полем, тогда Р’ называют подполем поля Р, а Р – расширение поля Р’.

Характеристика поля; ее простота. Будем обозначать сумму n – единиц 1+1+..+1=n*1. Наименьшее натуральное число n, такое что n*1=0 называется характеристикой поля. Если при любом n, n*1 не = 0, то говорят что характер-ка поля равна нулю.

Замечание:  поля характеристики нуль. Прим: рац. числа, комплек-х, множ-во A <0,1>характеристика 2.

Теорема: Если поле P имеет конечную характеристику n, то n простое число.

Замечание: Из Т. не следует сущест-е полей характе-ки p, где p – простое число, а следует лишь, что не существует полей составных характеристик.

Подполя и расширения полей.

Пусть в поле P некоторая часть его элементов, составляющая множество P’, сама оказывается полем по отношению к тем операциям, которые определены в поле Р, т.е. для a,b прин P’ содержащиеся в поле P элементы a+b,ab,a-b и, при b0, a/b принадлежат к P’. Тогда P’ называется подполем поля Р, а Р – расширением поля P’. Понятно, что нуль и 1 поля Р будут содержаться в поле Р’ и служить для P’ нулем и единицей. Так, поле рациональных чисел явл-ся подполем поля действительных чисел; все числовые поля будут подполями поля комплексных чисел.

Изоморфизм колец (полей). Два кольца К и К’ (поле Р и P’) называются изоморфными, если  взаимно однозначное отображение и К->K’ (P->P’), что для  элементов из К (Р) выполняются равенства:

Пример: пусть К – множество всех действительных чисел (К->R), K’ –множество всех точек на прямой. Сложение для точек на прямой введем сложение как сложение векторов, а умножение, как умножение модулей.

В качестве взаимного отображения  можно выбрать следующее правило – каждому действительному числу ставим в соответствие точку удаленную от фиксированного начала координат на к единиц.

Пример: Множество точек на плоскости и комплексные числа.

Источник

Делители нуля

В абстрактной алгебре, ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.

Правый делитель нуля определяется аналогично: ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.

Элемент, который является и правым и левым делителем нуля одновременно называется делителем нуля. Если умножение в кольце коммутативно тогда правые и левые делители совпадают. Ненулевые элементы кольца, которые не являются ни правыми, ни левыми делителями нуля называются обычными элементами.

Пример: в кольце элементы 2, 3, 4 — делители нуля.

Ассоциативное и коммутативное кольцо с единицей 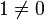без делителей нуля называется областью целостности.

Внешние ссылки

Смотреть что такое «Делители нуля» в других словарях:

Делитель нуля — В абстрактной алгебре ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0. Аналогично, ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0 … Википедия

АЛГЕБРА АБСТРАКТНАЯ — (общая алгебра), раздел современной математики, выросший из исследования уравнений и теории чисел. Свою теперешнюю форму абстрактная алгебра начала приобретать лишь в двадцатом веке. Занимается главным образом изучением систем, элементы которых… … Энциклопедия Кольера

ДВОЙНЫЕ И ДУАЛЬНЫЕ ЧИСЛА — гиперкомплексные числа вида a+bе, где аи b действительные числа, и для двойных чисел е 2= + 1, а для дуальных чисел е 2=0. Сложение Д. и д. ч. определяется формулой Умножение двойных чисел производится по формуле а дуальных чисел по формуле… … Математическая энциклопедия

Двойные числа — О гиперкомплексных числах параболического типа см. дуальные числа Двойные числа или паракомплексные числа, расщепляемые комплексные числа, комплексные числа гиперболического типа гиперкомплексные числа вида « », где и вещественные… … Википедия

Процедура Кэли — Диксона (процедура удвоения) это рекурсивная процедура построения алгебр над полем вещественных чисел, с удвоением размерности на каждом шагу. Названа в честь Артура Кэли и Леонарда Диксона. Эта процедура позволяет построить комплексные числа,… … Википедия

АЛЬТЕРНАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — Альтернативным кольцом (А. к.) наз. кольцо, в к ром каждые два элемента порождают ассоциативное подкольцо; альтернативной алгеброй (А. а.) наз. линейная алгебра, являющаяся А. к. Согласно теореме Артина класс всех А. к. задается системой тождеств … Математическая энциклопедия

АССОЦИАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ — кольца и алгебры с ассоциативным умножением, т. е. множества с двумя бинарными операциями сложением + и умножением Х, являющиеся абелевой группой по сложению и полугруппой по умножению, причем умножение дистрибутивно (слева и справа) относительно … Математическая энциклопедия

ВИТТА КОЛЬЦО — поля k, кольцо типов квадратичных форм над k, кольцо W(k).классов невырожденных квадратичных форм на конечномерных векторных пространствах над kпо следующему отношению эквивалентности: форма f1 эквивалентна форме тогда и только тогда, когда для… … Математическая энциклопедия

ГРУППОВАЯ АЛГЕБРА — группы G над полем K ассоциативная алгебра над полем К, элементами к рой являются всевозможные формальные конечные суммы вида а операции определяются формулами: (в правой части второй формулы сумма также конечна). Эта алгебра обозначается… … Математическая энциклопедия

Источник

О том, как правильно понимать определитель матрицы

Расшифровывается это дело следующим образом: если у нас есть матрица

над некоторым полем , то определителем этой матрицы называют сумму всевозможных произведений, состоящих изэлементов этой матрицы, взятых по одному из каждой строки и из каждого столбца, причем каждое произведение входит в эту сумму с тем знаком, который имеет соответствующая перестановка индексов этих элементов в этом произведении.

Другой способ введения определителя связан с его характеристическим свойством. Напомним, полилинейной формой называется функция , определенная на декартовом произведении некоторых векторных пространств (заданных над одним и тем же полем), принимающая значения в поле и линейная по каждому аргументу: . Форма называется кососимметрической, если при инверсии любых двух (не обязательно соседних) аргументов она меняет знак.

Можно конечно всюду далее рассматривать исключительно поля характеристики 2 и пользоваться «слабым» определением кососимметричности, а можно поступить умнее и немного усилить определение кососимметричности специально для полей характеристики 2 так, чтобы обычная кососимметричность следовала из «сильной». Для этого достаточно потребовать 2 вещи: во-первых, форма должна быть полилинейна, а во-вторых она должна принимать значение ноль всегда, когда среди ее аргументов есть равные. Свойство, которое вытекало из «наивной» кососимметричности для полей характеристики 2 само теперь является составной частью определения кососимметричности (правда только для полей характеристики 2).

Из полилинейности и равенства формы нулю на строках с равными аргументами следует, что если к одному вектору прибавить другой, умноженный на число, то значение формы не изменится. При умножении какого-либо вектора на число 0 сама форма умножается на это число (в частности, если обратить знак какого-либо вектора из набора, то знак самой формы тоже поменяется.

Произвести инверсию векторов в наборе аргументов можно с помощью преобразований этих двух типов. И если внимательно проследить цепочку преобразований, то в конце концов окажется, что форма поменяла знак.

Далее под кососимметричностью будем понимать кососимметричность в «сильном» смысле.

Определение

Определитель матриц— это единственная кососимметрическая полилинейная форма строк матрицы, нормированная единицей на единичном наборе векторов.

Надо сказать, это не самое плохое определение. Но и оно не лишено недостатков. Основные вопросы здесь возникают по поводу кососимметричности. В первую очередь непонятно, почему это свойство вообще важно. Ну меняет функция знак при перестановке двух аргументов и пусть меняет, почему мы так стремимся исследовать именно это свойство, а не какое-нибудь другое. Но здесь все еще хуже. Мы хотим, чтобы форма еще и принимала нулевое значение на наборе, содержащем равные вектора. И в некотором смысле для нас это даже важнее самой кососимметричности, раз мы стали подгонять определение последней под выполнение этого свойства. Все эти экзерсизы с характеристиками выглядят довольно искусственно.

В действительности есть очень простой и естественный пусть построения определителя, при котором все эти вопросы отпадают сами собой. И я постараюсь по возможности максимально последовательно описать этот способ.

Начнем с некоторых предварительных замечаний. Основным объектом изучения линейной алгебры являются конечномерные векторные пространства. Неформально говоря, на любое — мерное векторное пространство над полемможно смотреть как на «координатное» пространство, состоящее из упорядоченных наборов длины элементов поля. Более строго, пусть у нас есть— мерное векторное пространство над полем . Выбор (упорядоченного) базиса этого пространства индуцирует изоморфизм , ставящий в соответствие каждому вектору набор его координат в базисе . Таким образом, во всех дальнейших построениях речь пойдет по большей части про вектора координатного пространства.

Очевидно, некоторый набор векторов пространства является линейно (не)зависимым, тогда и только тогда, когда соответствующий ему набор векторов пространства будет линейно (не)зависимым.

Свойство линейной зависимости/независимости действительно очень важно. Дело в том, что система из 1″ alt=»n>1″ src=»https://habrastorage.org/getpro/habr/upload_files/4e1/89f/e1d/4e189fe1dc9b6260122146ddfd0031b7.svg»/>векторов пространства будет линейно зависимой тогда и только тогда, когда найдется вектор в этой системе, который можно линейно выразить через остальные.

Довольно естественным выглядит желание иметь некоторую функцию— индикатор линейной зависимости векторов. Учитывая, что любое векторное пространство «оцифровывается» своим координатным пространством, достаточно иметь такую функцию, определенную на декартовом произведениикопий пространстваи принимающую значения в поле. Таким образом, мы предъявляем к функциивсего лишь 2 очень естественных требования:

Она должна принимать нулевое значение на любой линейно зависимой системе векторов.

На аргументы этой функции удобно смотреть как на строки матрицы

Заметим, на данном этапе мы еще даже не знаем, существует ли такая функция или нет. Но мы можем в предположении ее существования посмотреть на ее поведение.

. Действительно, строка аргументов, содержащая пару равных значений, очевидно, линейно зависима, а значит функциябудет принимать на ней нулевое значение.

кососимметрична (в любом смысле, учитывая полилинейность + п.1). Доказательство абсолютно аналогично тому, которое находится выше под спойлером.

Рассмотрим, чему равнана некотором наборе строк :

Здесь мы просто выразили векторы через единичные, затем по полилинейности получили сумму по всем упорядоченным наборам соответствующих произведений, выкинули из них те, которые содержат повторяющиеся аргументы (тем самым получив сумму по всем перестановкам), а затем применили обратные перестановки к единичным векторам.

Смотрим на последнюю строчку в получившейся формуле и видим множитель . Чтобы упростить формулу и не таскать лишний множитель, добавим к тем 2 требованиям к функциитретье требование: .

Таким образом, если интересующая нас функциясуществует, то она имеет вид:

Нарисовалась знакомая нам формула Лейбница. Самое замечательное то, что в ней нет свободных переменных, а это значит, что мы бесплатно получили единственность интересующей нас функции.

Осталось лишь доказать существование. Капитан намекает, что для этого достаточно взять ту функцию, которая у нас получилась.

А дальше дело техники. Проверяем, что получили мы действительно, что хотели и даже больше. Полученную функцию называем определителем и спокойно приступаем к доказательству основных его свойств.

Источник