Под весом n 1 ой акции портфеля в модели у шарпа подразумевается
Модель У. Шарпа как альтернатива модели Марковица
Добрый день, уважаемое сообщество трейдеров, инвесторов и всех кто интересуется рынком ценных бумаг!
Модель У. Шарпа или как её ещё называют часто рыночная модель была впервые предложена американским экономистом, лауреатом Нобелевской премии Уильямом Форсайтом Шарпом в середине 60-х годов прошлого столетия.

Уильям Ф. Шарп является в настоящее время почетным профессором Высшей школы бизнеса Стэнфордского университета.
В 1990 г. он получил Нобелевскую премию по экономике, которую он получил за развитие теории оценки финансовых активов.
Он является одним из трех авторов одного из самых популярных в мире фундаментального учебника по курсу «ИНВЕСТИЦИИ«.
В модели Шарпа представлена зависимость между ожидаемой доходностью актива и ожидаемой доходностью рынка. Предполагается, что доходность обыкновенной акции за определенный период связанна с доходностью за аналогичный период с доходностью рыночного индекса. В этом случае с ростом рыночного индекса, вероятно, будет расти и цена акции и наоборот.
Таким образом данная модель предполагается линейной. А уравнение предложенной модели имеет следующий вид:
Главное отличие модели У. Шарпа от модели Г. Марковица состоит в следующем:
Модель Шарпа рассматривает взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом, в то время как модель Марковица — рассматривает взаимосвязь доходностей ценных бумаг между собой.
Именно для того, чтобы избежать высокую трудоемкость модели Марковица Уильям Шарп предложил рыночную (индексную) модель. При этом модель Шарпа это не новый метод составления портфеля ценных бумаг — это упрощенная модель Марковица, где решение проблемы выбора оптимального портфеля осуществляется с меньшими усилиями. Модель Шарпа обычно применяют при рассмотрении большого количества ценных бумаг, которые представляют значительную часть рынка.
Весьма интересным представляется сравнение результатов полученных по модели Марковица и модели Шарпа.
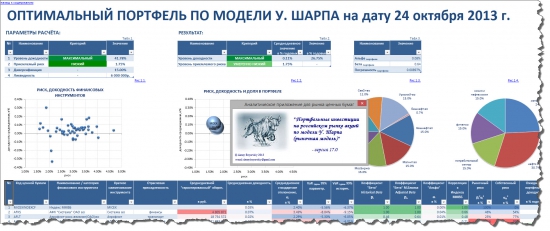
Для этого мной было разработано приложение, в Microsoft Office Excel*, под названием — «Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)«.
Полученный результат по указанным моделям Вы можете видеть ниже:
Итоговые параметры следующие:
Модель Марковица: 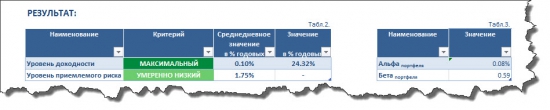
Модель Шарпа:
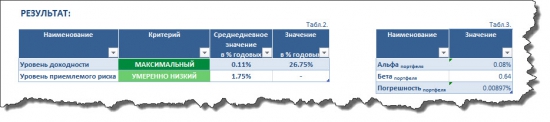
Здесь мы наблюдаем, что при одинаковом уровне риска доходность портфеля Шарпа оказывается несколько выше доходности по модели Марковица — 26,75% против 24,32% годовых, соответственно. При этом мы видим, что бета портфеля по модели Шарпа также выше беты получаемой по модели Марковица (0,64 против 0,59), а это, в свою очередь говорит о том, что портфель Шарпа является чуть менее оборонительным (защитным), чем портфель Марковица.
Рыночная модель У. Шарпа оптимального портфеля в итоге выглядит следующим образом:
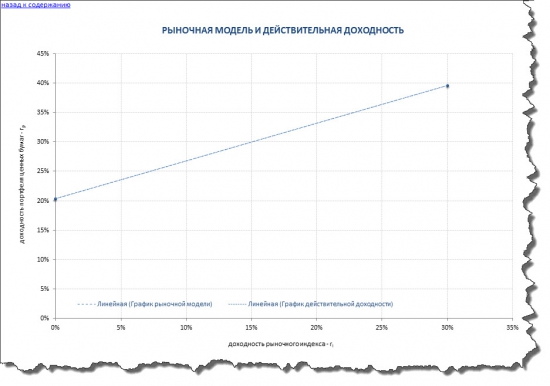
Все остальные расчетные показатели в представленном приложении «Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)» являются такими же как и в модели Марковица.
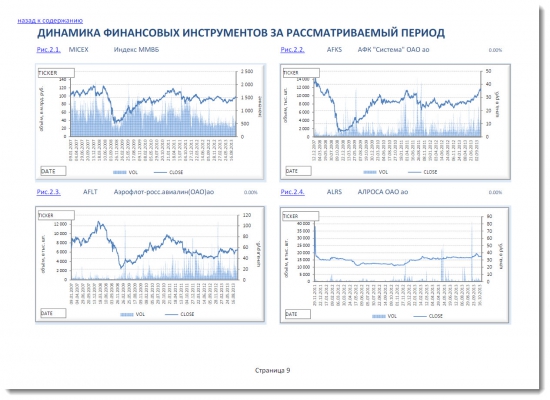
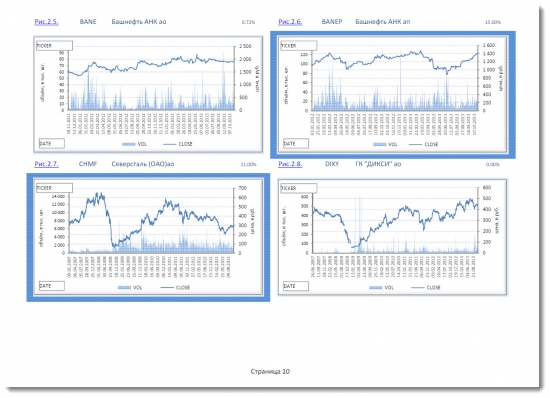
Приложение «Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)» содержит также те же технические характеристики, что и приложение «Портфельные инвестиции на российском рынке акций по модели Марковица»
Приложение настроено так, что Вы легко сможете распечатать все листы (нет необходимости специально форматировать их), чтобы делать для себя специальные папки куда вы можете подшивать Ваши расчеты и т.д. и т.п. Все страницы пронумерованы.
Также Вы сможете, при желании, преобразовать его в удобный, читаемый PDF формат (при наличии специальной программы для создания PDF файлов).
Для наглядности я выложил итоговый файл с данными, преобразованный в PDF формат, на общем диске. Вы можете пройти по ссылке и посмотреть либо скачать:
Все формулы в приложении открыты так, что Вы можете заглянуть в глубь самих расчетов в части использованных в приложении различных показателей.
При желании исходную базу данных приложения о ценовых параметрах, уже включенных в него финансовых инструментов, можно изменить, расширить (как по перечню рассматриваемых бумаг, так и по горизонту их исследования) и конечно же периодически обновлять приложение на текущую дату.
В условиях развитых и стабильно функционирующих фондовых рынков вышеупомянутые классические модели Марковица и Шарпа работают вполне эффективно. При этом в современных условиях применение лишь отдельно взятой модели не является правильным. Модели У. Шарпа и Г. Марковица могут являться хорошим дополнением к другим факторам при составлении оптимального портфеля ценных бумаг.
«Портфельные инвестиции на российском рынке акций по модели У. Шарпа (рыночная модель)» — это отличный инструмент для профессионального подхода к инвестированию на рынке ценных бумаг.
Если Вас заинтересовало приложение, то его можно приобрести либо на сайте:
Либо в качестве альтернативного варианта для приобретения Вы можете обратиться ко мне письмом на адрес alexeyboyarskiy@gmail.com
Всем удачной торговли!
* Для корректной работы журнала необходима версия Excel 2010 и выше.
Как оценить инвестиционный портфель по модели Шарпа?
Научитесь строить финансовые модели компаний из разных отраслей, отбирать эффективные инвестиционные инициативы и осуществлять сделки.
Основной целью любого инвестора является получение прибыли. Однако, чтобы достичь эту цель, следует грамотно составить инвестиционный портфель.
Для начала необходимо иметь четко представление, что из себя представляет инвестиционный портфель. Прежде всего, это совокупность ценных бумаг, приобретаемых инвестором в ходе активных операций по вложению капитала в прибыльные объекты. Инвестиционные активы могут быть разными: начиная от акций и облигаций, заканчивая недвижимостью и автомобилями
Каждый инвестор самостоятельно выбирает свою инвестиционную стратегию. Кто-то вкладывается в проверенные и менее рискованные проекты, жертвуя высокой прибыльностью. Другие же, наоборот, предпочитают вкладывать свои средства в краткосрочные и прибыльные дела, рискуя потерять их в случае провала.
Многие начинающие инвесторы задаются вопросом, из каких ценных бумаг можно сформировать свой инвестиционный портфель и каким образом оценить правильность этого составления. Одним из способов оценки инвестиционного портфеля является модель Шарпа. Познакомиться с другими концепциями, которые применяются в финансовом анализе, можно на нашем открытом онлайн-курсе «Финансы с нуля».
Как известно, чем выше риск, тем выше прибыльность от использования инвестиционной стратегии. Иногда существует грань, за которой риск получить убыток выше вероятности получения прибыли. Именно для этого и применяют модель Шарпа.
Коэффициент Шарпа — это параметр, который показывает, насколько доход от стратегии соотносится к потенциальному риску.
rp — доход за фиксированный период
rf — безрисковый доход
σp — стандартное отклонение доходности портфеля
Доходность портфеля представляет собой взвешенную сумму среднеарифметических дневных доходностей, а риск портфеля равен взвешенной сумме стандартных отклонений доходностей акций.
За безрисковую доходность часто берут среднюю ставку доходности 10 летних облигаций федерального займа. Используя эти показатели, можно определить коэффициент Шарпа.
Если значение данного индекса больше 1, то выбранная стратегия является хорошей, а результативность управления портфелем — высокая.
Если же значение показателя Шарпа колеблется в интервале от 0 до 1, то уровень риска выше, чем достаточная доходность. Инвестировать в такой проект можно, но он не принесет достаточной прибыльности.
И, наконец, если значение показателя Шарпа будет меньше 0, то целесообразнее пересмотреть активы в инвестиционном портфеле или вложить их в безрисковый актив, например, облигации федерального займа.
Для знакомства с моделью Шарпа я составила инвестиционный портфель из акций пяти известных российских компаний: Сбербанк, ВТБ, Алроса, Росбанк, Московский кредитный банк. Вы можете составить портфель любым способом, каким захотите, с любым количеством компаний.
Для анализа я решила использовать данные за 3 года по месяцам (табл. 1), однако для более точного анализа можно увеличить рассматриваемый диапазон и частоту.
Выгружаем данные в Excel. Подробное руководство по правильной выгрузке данных смотрите в файле, который прикреплен к посту («Алгоритм действий»).
Далее необходимо рассчитать доли акций каждой компании в общем портфеле (табл. 2).
А затем следует рассчитать доходность по каждой ценной бумаге портфеля (табл.3). Для этого воспользуемся формулой в Excel:
Доходность акции = LN (Предыдущий период/Отчетный период)
Доходность акции Сбербанка = LN(B3/B2) = 8,8%
Доходность акции ВТБ= LN(С3/С2) = 6,4%
Доходность акции МКБ = LN(D3/D2) = 0,6%
Доходность акции Алросы= LN(Е3/Е2) = 7,5%
Доходность акции Росбанка= LN(F3/F2) = 8,2%
Далее рассчитаем доходность портфеля, риск портфеля и безрисковую доходность (табл.4). Безрисковая доходность была взята как средняя доходность по 10-летним ОФЗ и составляет 8,7%. Для расчета использованы следующие формулы:
Доходность портфеля = Сумма (СРЗНАЧ(Диапазон доходности i-ой компании) × Доля i-ой компании в портфеле)
Риск портфеля = Сумма (СТАНДОТКЛОН(Диапазон доходности i-ой компании) × Доля i-ой компании в портфеле
Коэффициент Шарпа = (Доходность портфеля — Безрисковая доходность) / Риск портфеля
Следует заметить, что индекс получился отрицательным за счет того, что доходность каждой ценной бумаги, а следовательно, и самого портфеля, намного меньше безрисковой доходности.
Чтобы получить положительный показатель Шарпа, следует на ранней стадии выбора состава инвестиционного портфеля отобрать такие ценные бумаги, чтобы уровень доходности портфеля превышал безрисковую доходность.
Также, для более точного анализа следует взять котировки акций за большой промежуток времени и периодичность. В этом случае можно в полной мере выявить эффективность инвестиционного портфеля.
Основным преимуществом анализа инвестиционного портфеля индексом Шарпа является наглядность прибыльности той или иной ценной бумаги. Данный метод позволяет рассмотреть характер доходности портфеля – плавную или скачкообразную.
Однако и такой анализ не лишен недостатков:
Но несмотря на наличие некоторых недостатков, коэффициент Шарпа позволяет выявить наиболее доходные инвестиционные стратегии при составлении портфеля. Данный метод можно комбинировать с другими видами инвестиционного анализа для составления более точного представления о сформированном портфеле.
Автор: Дарина Есенгулова, Mazars, consulting
Научитесь строить финансовые модели компаний из разных отраслей, отбирать эффективные инвестиционные инициативы и осуществлять сделки.
Оптимизация инвестиционного портфеля по модели Шарпа
Выведенные Марковицем правила построения границы эффективных портфелей позволяет находить оптимальный (с точки зрения инвестора) портфель для любого количества ценных бумаг в портфеле. Основной сложностью применения метода Марковица является большой объем вычислений, необходимый для определения весов Wi каждой ценной бумаги. Действительно, если портфель объединяет n ценных бу маг, то для построения границы эффективных портфелей необходимо предварительно вычислить n значений ожидаемых (средних арифметических) доходностей E ( ri ) каждой ценной бумаги, n величин с 2 i диспер сий всех норм отдачи и n(n1)/2 выражений попарных ковариаций ai j ценных бумаг в портфеле.
В 1963 г. американский экономист У. Шарп ( William Sharpe ) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как однондексная модель Шарпа ( Sharpe singleindex model ).
где: ri t доходность i ой ценной бумаги в момент времени t (например, 31 декабря 2000 года);
P i параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i ой ценной бумаги к изменениям рыночной доходности;
rm t доходность рыночного портфеля в момент t ;
sit случайная ошибка, свидетельствующая о том, что реальные, действующие значения ri t и rm t порою отклоняются от линейной зависимости.
Оценка результатов регрессии. Параметры α i и β i регрессионной модели дают представление об общих тенденциях взаимосвязей между
Определение параметров ai и № регрессионной модели. Для на хождения параметров a i и P i по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров a i и P i берутся такие значения, которые минимизируют сумму квадратов ошибок в. Если провести необходимые вычисления, то окажется, что параметры a i и P i принимают следующие значения:
Кроме того, точность регрессии можно определить, оценивая, сколь точно регрессионная модель определяет дисперсию а] ценных бумаг, для
которых составляется регрессионная модель.
Дисперсию ценной бумаги а] можно представить в виде двух слагаемых:
В этом случае первое слагаемое будет показывать, какую долю в общем риске ценной бумаги можно описать с помощью регрессионной модели ( ri t = a i + P irm t ), а второе слагаемое степень неточности регрессионной модели. Значит, чем ближе величина ^а 2 /а] ближе к единице, тем более точная регрессионная модель.
Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значения дисперсий ^ случайных
ошибок, mo вычислим их. Общая формула для вычисления дисперсии случайной ошибки имеет вид:
В данном случае средняя арифметическая величина вычисляется делением на ( N 2), поскольку две степени свободы были утеряны при вычислении a i и P i.
Использование рыночной модели Шарпа для построения границы эффективных портфелей. Одно из главных достоинств модели Шарпа состоит в том, что она позволяет значительно сократить объемы вычислений при определении оптимального портфеля, давая при этом результаты, близко совпадающие с получаемыми по модели Марковица. Поскольку в основу модели Шарпа положена линейная регрессия, то для ее применения необходимо ввести ряд предварительных условий. Если предположить, что инвестор формирует портфель из ценных бумаг, то будем считать, что:
2) Дисперсия случайных ошибок σε 2 , i для каждой ценной бумаги постоянна.
3) Для каждой конкретной ценной бумаги отсутствует корреляция между наблюдаемыми в течение N лет величинами случайных ошибок.
4) Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле.
5) Отсутствует корреляция между случайными ошибками ε i и рыночной доходностью.
Используя эти упрощения, можно получить выражения E ( ri ), σ i 2 и
Подведем итог: если инвестор формирует портфель из n ценных бумаг, то использование параметров линейной регрессии a i и P i позволя ет выразить с их помощью все начальные элементы ожидаемую доход ность E( ri ) каждой ценной бумаги в портфеле, дисперсии а 2 и ковариа
6) Подставить эти значения в уравнения (7.15 – 7.18)
После такой подстановки выяснится, что неизвестными величина ми являются веса Wi ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля E *, можно найти веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.
Инвестиционная деятельность. Вопрос 1 й в линейном регрессионном анализе предполагается, что средняя арифметическая величина случайной ошибки
В линейном регрессионном анализе предполагается, что средняя арифметическая
величина случайной ошибки …
В модели Г. Марковица предполагается, что …
цены акций изменяются случайным образом
В общем случае в инвестиционный портфель могут входить…
ценные бумаги и нефинансовые активы
В общем случае ожидаемая доходность случайной ошибки любой акции портфеля E(i) = 0.
Тогда утверждать, что и дисперсия случайной ошибки для любой акции портфеля в
модели Шарпа также равна нулю в общем случае …
В общем случае ставка дисконта определяет:
В процессе формирования инвестиционного портфеля может использоваться…
Выбрать тип ценных бумаг для их включения в портфель можно по степени риска и …
в зависимости от источника доходов по ценным бумагам портфеля
Выделяют следующие виды управления инвестиционным портфелем:
активное и пассивное
Глобальный проект с положительной общественной эффективностью был, в конечном
итоге, отвергнут фирмой. Причиной этому могли послужить следующие обстоятельства,
связанные с оценкой эффективности проекта:
отрицательная коммерческая эффективность даже с учетом поддержки проекта
Дисперсия портфеля принимать отрицательное значение …
Для локальных проектов оценка их эффективности по правилу NPV может быть
Для нахождения коэффициентов и регрессионной модели используется метод
наименьших квадратов. Это означает, что при вычислении данных коэффициентов
была минимальной сумма квадратов случайной ошибки
Для придания компактности формулам, с помощью которых строится граница
эффективных портфелей, У. Шарп предложил ввести понятие (n+1)-ой акции портфеля.
Под этой акцией понимается …
рыночный портфель в целом
Если NPV проекта положительная, то сальдо накопленных денег В(k) на любом шаге
может быть и положительным, и отрицательным
Если веса акций портфеля положительные, то ожидаемая доходность портфеля…
может быть и положительной, и отрицательной
Если для какой-то акции коэффициент «бета» оказывается меньше нуля, то коэффициент
«альфа» в этом случае…
может быть как больше нуля, так и меньше нуля
b= 1,1, то можно утверждать, что …
более чувствительной к изменениям рынка является акция B
Если инвестор располагает 25 акциями «Газпрома», 10 векселями Сбербанка и 15
облигациями сберегательного займа, то считать, что он сформировал портфель ценных
можно, если совокупностью этих ценных бумаг он управляет как единым целым
Если инвестор сформировал «портфель роста», то …
он рассчитывает на рост курсовой стоимости ценных бумаг портфеля
Если инвестор сформировал портфель из государственных облигаций с целью получения
стабильного дохода, то по склонности к риску такого инвестора, скорее всего, можно
Если ожидаемая доходность портфеля является средневзвешенной величиной доходности
входящих в портфель ценных бумаг, то в общем случае риск портфеля взвешенной
средней величине дисперсий доходности ценных бумаг портфеля …
не равен, поскольку на риск портфеля оказывают влияние ковариации доходностей
Если при вычислении NPV проекта начальные инвестиционные затраты C0 складываются
с величиной PV проекта, а не вычитаются, то:Ответ:
такого не может быть
Если принятие проекта А не воздействует на потоки денег по другому проекту В, то такие
Если произойдет одновременное увеличение дебиторской задолженности и уменьшение
кредиторской задолженности, то это будет учитываться как:
отток от инвестиционной деятельности
Если случайная ошибка в регрессионном уравнении является случайной величиной, то
ее средняя арифметическая величина принимать отрицательное значение …
Если фирма при оценке NPV проекта выберет шаги расчета разной длительности, то:
необходимо провести коррекцию ставок дисконта и вычислить NPV
Заданному уровню риска единственная точка на границе эффективных портфелей
не всегда, поскольку одному уровню риска могут соответствовать две точки на границе
Из перечисленного ниже можно отнести к объектам капитальных вложений:
Известно, что в основе метода У. Шарпа лежит метод линейного регрессионного анализа.
Уравнение линейной регрессии в данной модели связывает …
доходности конкретной акции портфеля и доходности рыночного портфеля
Имеется инвестиционный проект, рассчитанный на 1 год, с начальными
инвестиционными затратами С0, осуществляемыми 09 марта. Через год от этого проекта
ожидается доход С1. Можно оценить экономическую эффективность данного проекта,
приведя обе суммы С0 и С1 к какой-нибудь промежуточной дате, например, 25 июля:
Имеется инвестиционный проект, рассчитанный на 1 год, с начальными
инвестиционными затратами С0. Через год от этого проекта ожидается доход С1. Если
предположить, что за год общий уровень цен не изменится, то есть инфляции не будет, то
можно оценить эффективность этого проекта путем прямого сравнения сумм С0 и С1 без
их приведения к одной дате:
нет, поскольку на временную стоимость денег оказывает воздействие не только инфляция,
поэтому и без учета инфляции суммы С0 и С1 будут выражаться в разных рублях
Имеется общественно значимый проект. Проведенные вычисления показывают, что его
общественная эффективность отрицательная. Проектоустроителям в этом случае
Имеется проект длительностью 2 шага расчета, инвестиционные затраты С0=100 тыс.
рублей, а потоки денег по шагам расчета С1=(+50 тыс. рублей) и С2=(+80 тыс. рублей).
Если ставка дисконта не изменится, а потоки денег поменяются местами: С1=(+80 тыс.
рублей) и С2=(+50 тыс. рублей), то величина NPV:
Имеются два инвестиционных проекта А и В. Пусть для проекта А ставка дисконта
два проекта, то NPV совместного проекта равнялась:
— Какой из этих проектов следует принимать при оценке по правилу IRR?
Имеются два проекта А и В, потоки денег по которым приведены ниже:
Если приемлемая ставка дисконта составляет 19%, то какой из проектов можно принять
на основании правила IRR?
Инвестиционная фаза проекта может предшествовать прединвестиционной фазе:Ответ:
Инвестор выбрал n акций и путем перебора их весов построил зону существования
портфелей. Ситуация, чтобы для какого-то портфеля, сформированного из этих акций,
соответствующая точка на координатной плоскости [; E(r)] лежала вне данной зоны …
Инвестор может выполнять функции подрядчика:
да, если это не запрещено законом или контрактом
Инвестор намерен оценить доходность акции за будущий холдинговый период с помощью
ожидаемой доходности E(r). С этой целью он выбрал 8 шагов расчета в прошлом, за
которые намерен вычислить доходность rt этой акции. Для вычисления E(r) брать шаги
расчета различной длительности …
нельзя, поскольку шаги расчета должны быть одинаковой длительности, равной
Инвестор намерен оценить ожидаемую доходность E(r) акции за холдинговый период.
Для этого он выбрал N = 10 шагов в прошлом, высчитал доходность акции за каждый шаг
расчета и нашел E(r). Ситуация в которой E(r) будет отрицательной величиной …
возможна, E(r) может быть 0:
да, такое может произойти
Может сложиться ситуация, что для одного проекта возрастание темпов инфляции
повысит его эффективность, а для другого – понизит:
да, это может наблюдаться при различном воздействии инфляции на оборотные средства
Можно оценить по правилу срока окупаемости приемлемость двух проектов А и В,
да, это можно делать
На графике граница эффективных портфелей в модели Шарпа строится в координатах,
Ответ: теми же, что и в модели Марковица
Несколько физических лиц решили создать Общественное объединение любителей театра.
Данное Объединение не имеет статуса юридического лица и представляет «клуб по
интересам». Данное объединение выступать в качестве инвестора …
Облигации могут являться капитальными вложениями:
могут, если они вкладываются в объекты капитальных вложений
Общественно значимый проект может иметь отрицательную общественную
Одним из условий эффективности рынка ценных бумаг по теории Марковица является:
отсутствие ассиметрии информации
Отдельные методы оценки эффективности инвестиционных проектов основываются на
методе приведения потоков денег к одной дате, поскольку:
приведенная стоимость позволяет учесть распределение во времени потоков денег
Оттоки от операционной деятельности связаны с затратами на:Ответ:
оплату арендной платы используемого оборудования
Оценивать эффективность участия конкретной фирмы в проекте необходимо:
только в том случае, если этот проект эффективен в целом
Оцениваются два проектаА и В, причем проект А является общественно значимым, а
Учитывается ли в этом случае ставка дисконта, и каким образом?
никак не учитывается
Оценка экономической эффективности инвестиционного проекта осуществляется на
Под «ожидаемой доходностью E(r)» отдельной акции в модели Г. Марковица понимается
средняя арифметическая величина наблюдавшихся ранее значений доходности акций
Под весом (n+1)-ой акции портфеля в модели У. Шарпа подразумевается …
соответствие затрат на проект и полученных от него результатов
может быть отрицательной величиной
Поступающая на рынок ценных бумаг информация …
воздействует на цены акций поскольку она определяет спрос на акции и их предложение,
изменение которых воздействует на цены акций
Представим, что руководство компании решило возвести новый цех и столовую для своих
рабочих. Эти проекты, скорее всего:
При вычислении NPV денежные суммы следует брать после уплаты соответствующих
да, денежные суммы берутся после уплаты налогов
При вычислении NPV первоначальные затраты на проект:
При оценке денежных потоков от ИП необходимо всегда учитывать фактор инфляции:
да, это общее правило
При оценке коммерчески эффективного проекта эффективность участия фирмы в проекте
оказалась отрицательной. Тогда необходимо:
При оценке реальных проектов ставка дисконта r определяет издержки упущенной
При оценке эффективности локального проекта установлено, что его NPV При какой ставке дисконта можно начинать реализовывать проект?
Проект имеет длительность 2 шага расчета. Тогда может сложиться ситуация, что за
да, такая ситуация может сложиться
Проект рассчитан на 10 шагов и для пятого шага сальдо накопленных денег В(5)