поле создано равномерно заряженной сферической поверхностью

Поле равномерно заряженной сферической поверхности

Поле равномерно заряженной сферической поверхности. Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью о. Поле в данном случае будет центрально-симметричным: Ё в любой точке проходит через центр шара; Е = Е(г) и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара сферу радиуса г (рис. 1.2.14).

Если г > R, то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда

Но внутри шара, при г q 4ле₀/* 2

Бесконечная равномерно заряженная плоскость (а — поверхностная плотность заряда)

Шар радиуса /?, заряженный равномерно с объемной плотностью р

Сфера радиуса R, заряженная равномерно с поверхностной плотностью заряда о

Бесконечно длинный цилиндр (нить), заряженный равномерно с объемной плотностью р (А, — линейная плотность заряда)

Формулы для расчета напряженности

График зависимости напряженности от координаты

Две бесконечно длинные паралель- ные плоскости, заряженные разноименно с одинаковой с

Бесконечно длинная тонкая равномерно заряженная прямая нить ( X = const)

Бесконечная равномерно заряженная по объему зарядом с р = const плоскопараллельная пластина толщиной d

Е =— при — р g d d Е =- при х —

Пондермоторные силы. Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин)

Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора равна F = 2 S/2e₀, где S — площадь обкладок конденсатора. Так как а = q/S = Ег₀, то формула для расчета пондермоторной силы имеет вид:

Источник

Применение теоремы Гаусса к расчету поля равномерно заряженной сферической поверхности

Рассмотрим сферическую поверхность (рис. 19) радиусом R (общий заряд Q), заряженную равномерно с поверхностной плотностью +ст [см. (12.1)]. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (см. рисунок).

Мысленно построим сферу радиусом г, имеющую общий центр с заряженной сферой. Поле является центрально-симметричным относительно центра сферы. Величина напряженности является функцией расстояния гот центра сферы и одинакова во всех точках, равноудаленных от ее сферы (одинакова во всех точках воображаемой сферы радиусом г).

Если г > Л, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (11.2),

Если г’ R поле убывает с расстоянием г по такому же закону, как у точечного заряда |см. (3.2)], а при г’ R, r_:> R, г, > г,), равна [см. (9.3)]

Если принять г, = г и г, = °°, то потенциал поля вне сферической поверхности, согласно формуле (14.2), задается выражением

[ср. с формулой (8.6)]. Внутри сферической поверхности потенциал всюду одинаков и равен

График зависимости ср от г приведен на рис. 21.

Применение теоремы Гаусса к расчету поля объемно-заряженного шара

Рассмотрим шар радиусом R (общий заряд Q), заряженный с объемной плотностью р |см. (11.3)| (рис. 22). Мысленно построим сферу радиусом г, имеющую общий центр с заряженным шаром. Поле — центрально-симметрично (центр шара — центр симметрии поля).

Как и в случае сферы [см. § 14],

Е одинакова во всех точках воображаемой сферы радиусом г.

Если г > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (11.2),

Таким образом, напряженность поля вне объемно-заряженного шара такая же, как и вне заряженной сферической поверхности [см. формулу (14.1)), что можно было и ожидать исходя из соображений симметрии.

Внутри шара напряженность поля будет другая. Сфера радиусом г’ R) вычисляется по формуле (15.1), совпадающей с формулой (14.1), поэтому разность потенциалов между двумя точками, лежащими на расстояниях г, и г, от центра шара (г, > R, г, > R, г, > г₍), определяется формулой (14.2):

Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях г <и г[ от центра шара (/?’ г,’), равна

Применение теоремы Гаусса к расчету поля равномерно заряженного бесконечного цилиндра

Рассмотрим бесконечный цилиндр радиусом R (рис. 24), равномерно заряженный с линейной плотностью т.

Линейная плотность заряда

— физическая величина, определяемая зарядом, приходящимся на единицу длины.

Из соображений симметрии следует, что линии напряженности будут направлены с одинаковой густотой вдоль радиальных прямых, перпендикулярных оси цилиндра. Напряженность Е может зависеть только от расстояния г от оси цилиндра.

В качестве замкнутой поверхности мысленно построим коаксиальный цилиндр радиусом г и

высотой / (см. рис. 24). Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2nrlE. По теореме Гаусса (11.2), при г > R

откуда

Если г R, г, > Л, г, > равна [см. (9.3)1

Источник

Учебники

Журнал «Квант»

Общие

§9. Электрическое поле и его свойства

9.7. Поле равномерно заряженной сферы

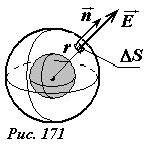
Рассмотрим теперь с помощью теоремы Гаусса, поле, создаваемое равномерно заряженной тонкой сферической оболочки. Опять начнем с рассмотрения симметрии поля. Очевидно, что поле, также как распределение зарядов имеет сферическую симметрию. Это означает, что модуль вектора напряженности зависит только от расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном расстоянии, модуль напряженности постоянен), а направление — радиальное, от центра сферы к точке наблюдения. Выберем в качестве замкнутой поверхности, к которой применим теорему Гаусса, сферу, концентрическую с заряженной оболочкой (рис. 171).

Пусть радиус сферы r больше радиуса оболочки. Тогда во всех точках этой сферы вектор напряженности направлен вдоль нормали к поверхности, а его модуль постоянен. Поэтому поток вектора напряженности через сферу равен произведению модуля напряженности на площадь сферы \(

Полученная формула, соответствует формуле закона Кулона для точечного заряда, следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем точечного заряда, помещенного в центре сферы. Таким образом, результат, на доказательство которого И. Ньютон затратил несколько лет, получен нами почти автоматически. Подчеркнем, что для доказательства формулы (1) помимо теоремы К. Гаусса, потребовалось рассмотреть симметрию поля.

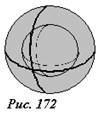
Поле внутри заряженной сферической оболочки также должно обладать сферической симметрией. Поэтому, поток вектора напряженности электрического поля через сферу, концентрическую с заряженной оболочкой и расположенную внутри нее (рис. 172) также выражается формулой \(

Однако внутри этой сферы электрических зарядов нет, поэтому, из теоремы К. Гаусса следует, что напряженность поля внутри сферы равна нулю. Подчеркнем, если бы теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки существовало бы электрическое поле.

Таким образом, функция, описывающая напряженность поля равномерно заряженной сферы радиуса R, имеет вид (график этой функции показан на рисунке 173)

Источник

§ 1.12. Поле заряженной плоскости, сферы и шара

Поле равномерно заряженной бесконечной плоскости

Когда заряд распределен по какой-либо поверхности, то для расчета полей удобно ввести поверхностную плотность заряда с. Выделим на плоской поверхности маленький участок площадью ΔS. Пусть заряд этого участка равен Δq. Поверхностной плотностью заряда называют отношение заряда Δq к площади поверхности, по которой он распределен:

Эта плотность может непрерывно изменяться вдоль поверхности. Конечно, электрический заряд имеет дискретную (прерывную) структуру, так как сосредоточен в элементарных частицах. Но если на поверхности площадью ΔS содержится огромное число элементарных зарядов, то дискретную структуру заряда можно не принимать во внимание. Мы ведь пользуемся понятием плотности, считая, что масса непрерывно распределена в пространстве. А на самом деле все тела состоят из дискретных образований — атомов.

В случае равномерного распределения заряда q по поверхности площадью S поверхностная плотность заряда постоянна и равна:

Рассмотрим бесконечную равномерно заряженную плоскость. Поверхностная плотность заряда σ известна. Из соображений симметрии очевидно, что линии напряженности представляют собой прямые, перпендикулярные плоскости. Поле бесконечной плоскости — однородное поле. Во всех точках пространства, независимо от расстояния до плоскости, напряженность поля одна и та же.

Для применения теоремы Гаусса нужно выбрать замкнутую поверхность таким образом, чтобы можно было легко вычислить поток напряженности электрического поля через эту поверхность. В данном случае удобнее всего выбрать цилиндр, образующие которого параллельны линиям напряженности электрического поля, а основания параллельны плоскости (рис. 1.43).

Тогда поток через боковую поверхность цилиндра будет равен нулю. Поэтому полный поток равен потоку через основания цилиндра А и В:

где Е_n — проекция вектора напряженности на нормаль к основанию цилиндра. Полный заряд внутри цилиндра равен σS. Согласно теореме Гаусса

Отсюда модуль напряженности равен:

В СИ эта формула принимает вид:

а в абсолютной системе

Поле равномерно заряженной сферы

Поток напряженности электрического поля через любую замкнутую поверхность внутри сферы равен нулю, так как равен нулю заряд. Это может быть лишь в том случае, когда напряженность поля внутри сферы равна нулю.

Найдем напряженность поля вне сферы. Из соображений симметрии ясно, что линии напряженности начинаются на поверхности сферы (в случае положительного заряда), направлены по радиусам сферы и перпендикулярны ее поверхности (рис. 1.44). Поэтому модуль напряженности поля одинаков во всех точках, лежащих на одинаковых расстояниях от центра сферы.

Проведем сферическую поверхность радиусом r > R, где R — радиус заряженной сферы. Поток напряженности через эту поверхность равен:

Если заряд сферы q, то по теореме Гаусса

Следовательно, модуль напряженности поля при r > R равен:

Таким образом, поле заряженной сферы совпадает вне сферы с полем точечного заряда, расположенного в центре сферы. График зависимости Е(r) изображен на рисунке 1.45.

Поле равномерно заряженного шара

Для характеристики распределения заряда по объему используется понятие объемной плотности заряда. Объемной плотностью заряда называется отношение заряда Δq к объему ΔV, в котором он распределен:

Эта плотность может непрерывно изменяться внутри заряженного тела. Если заряд q равномерно распределен по объему V, то объемная плотность заряда постоянна и равна:

Будем считать, что шар радиусом R равномерно заряжен; плотность заряда ρ известна. Полный заряд шара

Напряженность электрического поля вне шара можно найти с помощью теоремы Гаусса точно так же, как и напряженность равномерно заряженной сферы [см. формулу (1.12.9)]:

(при условии, что r > R). Поле аналогично полю точечного заряда q, расположенного в центре шара.

Для нахождения поля внутри шара нужно применить теорему Гаусса к потоку напряженности через сферическую поверхность радиусом к

Напряженность электрического поля линейно растет с увеличением расстояния вплоть до u = R. При r > R она определяется формулой (1.12.12). График модуля напряженности поля в зависимости от расстояния до центра представлен на рисунке 1.47.

Теорема Гаусса позволяет сравнительно просто определить напряженность электрического поля, если распределение заряда обладает определенной симметрией. Формулы (1.12.5), (1.12.9) и (1.12.15) следует запомнить. Их придется часто использовать.

Вопрос для самопроверки

* Мы предполагаем, что диэлектрическая проницаемость среды одинакова внутри и вне шара.

Источник

Элементарная физика

1.4 теорема остроградского-гаусса и применение ее для расчета электростатических полей

В соответствии с формулой (3.6) поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре (рис. 4.1), равен

Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 4.1) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

рис 4.1	рис 4.2

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 4.2), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока, в конечном счете, сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линий, входящих в поверхность. Если замкнутая поверхность не охватывает заряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

(4.1)

Знак потока совпадает со знаком заряда q.

Согласно (4.1), каждый из интегралов, стоящий под знаком суммы, равен . Следовательно,

(4.2)

При рассмотрении полей, создаваемых макроскопическими зарядами (т. e. зарядами, образованными огромным числом элементарных зарядов), отвлекаются от дискретной (прерывистой) структуры этих зарядов и считают их распределенными в пространстве непрерывным образом с конечной всюду плотностью. Объемная плотность заряда определяется по аналогии с плотностью массы как отношение заряда dq к физически бесконечно малому объему dV, в котором заключен этот заряд:

(4.3)

B данном cлyчае под физически бесконечно малым объемом нужно понимать такой объем, который с одной стороны, достаточно мал для того, чтобы плотность в пределах его можно было считать одинаковой, а с другой стороны, достаточно велик для того, чтобы не могла проявиться дискретность заряда.

Зная плотность заряда в каждой точке пространства, можно найти суммарный заряд, заключенный внутри замкнутой поверхности S. Для этого нужно вычислить интеграл ограниченному поверхностью:

(4.4)

Используя формулу (4.4), теорему Гаусса (4.2) можно записать так:

Теорема Гаусса позволяет в ряде случаев найти напряженность поля гораздо более простыми средствами, чем с использованием формулы (3.2) для напряженности поля точечного заряда и принципа суперпозиции полей. Рассмотрим применение теоремы Остраградского-Гаусса для расчета некоторых электростатических полей.

(4.5)

Здесь dq – заряд, заключенный в слое площади dS. Под dS подразумевается физически бесконечно малый участок поверхности.

Если заряд распределен по объему или поверхности цилиндрического тела (равномерно в каждом сечении), используется линейная плотность заряда

(4.6)

(dl – длина физически бесконечно малого отрезка цилиндра, dq – заряд, сосредоточенный на этом отрезке).

4.1. Поле равномерно заряженной бесконечной плоскости.

Бесконечная плоскость (рис. 4.3) заряжена с постоянной поверхностной плотностью +

. Согласно теореме Гаусса (4.2), (4.7) Из формулы (4.7) вытекает, что Е не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю и направлению, иными словами, поле бесконечно равномерно заряженной плоскости однородно. 4.2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 4.4). (4.8) Таким образом, результирующая напряженность поля между бесконечными разноименно заряженными плоскостями описывается формулой (4.8), а вне объема, ограниченного плоскостями, равна нулю. 4.3. Поле равномерно заряженной сферической поверхности. () (4.9) При r > R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 4.6. (Е = 0). 4.4. Поле объемно заряженного шара. () (4.10) Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (4.9), а внутри его изменяется линейно с расстоянием согласно выражению (4.10). График зависимости Е от r для рассмотренного случая приведен на рис. 4.7. 4.5. Поле равномерно заряженного бесконечного цилиндра (нити). Источник ← квартиры в орле северный район двухкомнатные Простор на дзержинского акции → Вам также понравится что означает татуировка бог 12.11.202303.04.2023 admin 0 Turn down for what slowed down 04.11.202321.08.2022 admin 0 что означает фамилия батухтин 10.11.202307.04.2023 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.