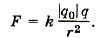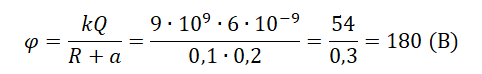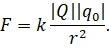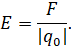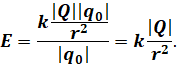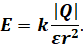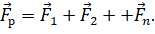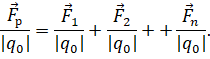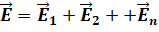поле точечного заряда и заряженного шара

§ 90. Поле точечного заряда и заряженного шара. Принцип суперпозиции полей

Что показывают силовые линии?

Для чего они используются?

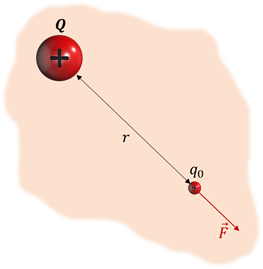
Напряжённость поля точечного заряда. Найдём напряжённость электрического поля, создаваемого точечным зарядом q₀. По закону Кулона этот заряд будет действовать на положительный заряд q с силой

Модуль напряжённости поля точечного заряда q₀ на расстоянии г от него равен:

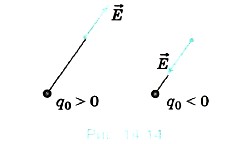
Вектор напряжённости в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис. 14.14), и совпадает с силой, действующей на точечный положительный заряд, помещённый в данную точку. Силовые линии электрического поля точечного заряда, как следует из соображений симметрии, направлены вдоль радиальных линий (рис. 14.15, а).

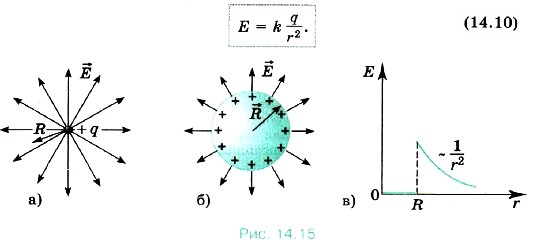
Поле заряженного шара. Рассмотрим теперь вопрос об электрическом поле заряженного проводящего шара радиусом R. Заряд q равномерно распределён по поверхности шара. Силовые линии электрического поля, также из соображений симметрии, направлены вдоль продолжений радиусов шара (рис. 14.15, б).

Распределение в пространстве силовых линий электрического поля шара с зарядом q на расстояниях r ≥ R от центра шара аналогично распределению силовых линий поля точечного заряда q (см. рис. 14.15, а). Следовательно, на расстоянии r ≥ R от центра шара напряжённость поля определяется той же формулой (14.9), что и напряжённость поля точечного заряда, помещённого в центре сферы:

Важно
Внутри проводящего шара (r Принцип суперпозиции полей

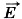
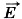
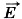
Если в данной точке пространства различные заряженные частицы создают электрические поля, напряжённости которых ₁, ₂, ₃ и т. д., то результирующая напряжённость поля в этой точке равна сумме напряжённостей этих полей:

Напряжённость поля, создаваемого отдельным зарядом, определяется так, как будто других зарядов, создающих поле, не существует.

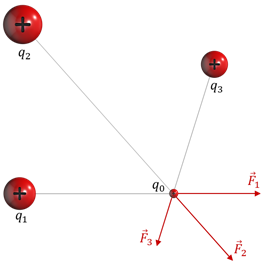
Согласно принципу суперпозиции полей для нахождения напряжённости поля системы заряженных частиц в любой точке достаточно знать выражение (14.9) для напряжённости поля точечного заряда. Для определения направления векторов напряжённостей полей отдельных зарядов мысленно помещаем в выбранную точку положительный заряд.

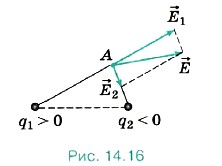
На рисунке 14.16 показано, как определяется напряжённость поля 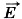в точке А, созданного двумя точечными зарядами q₁ и q₂.

Ключевые слова для поиска информации по теме параграфа.
Напряжённость. Силовые линии. Принцип суперпозиции полей

Вопросы к параграфу

1. Чему равна напряжённость поля заряженного проводящего шара?

2. Чему равна напряжённость поля точечного заряда?

3. Как направлена напряжённость поля заряда q₀, если q₀ > 0? если q₀

Источник

Поле точечного заряда и заряженного шара

Что показывают силовые линии?
Для чего они используются?

Напряжённость поля точечного заряда.

Найдём напряжённость электрического поля, создаваемого точечным зарядом q₀. По закону Кулона этот заряд будет действовать на положительный заряд q с силой

Модуль напряжённости поля точечного заряда q₀ на расстоянии г от него равен:

Вектор напряжённости в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис. 14.14), и совпадает с силой, действующей на точечный положительный заряд, помещённый в данную точку.

Силовые линии электрического поля точечного заряда, как следует из соображений симметрии, направлены вдоль радиальных линий (рис. 14.15, а).

Поле заряженного шара.

Рассмотрим теперь вопрос об электрическом поле заряженного проводящего шара радиусом R. Заряд q равномерно распределён по поверхности шара. Силовые линии электрического поля, также из соображений симметрии, направлены вдоль продолжений радиусов шара (рис. 14.15, б).

Распределение в пространстве силовых линий электрического поля шара с зарядом q на расстояниях r ≥ R от центра шара аналогично распределению силовых линий поля точечного заряда q (см. рис. 14.15, а). Следовательно, на расстоянии r ≥ R от центра шара напряжённость поля определяется той же формулой (14.9), что и напряжённость поля точечного заряда, помещённого в центре сферы:

Внутри проводящего шара (r

На рисунке 14.16 показано, как определяется напряжённость поля в точке А, созданного двумя точечными зарядами q₁ и q₂.

Источник

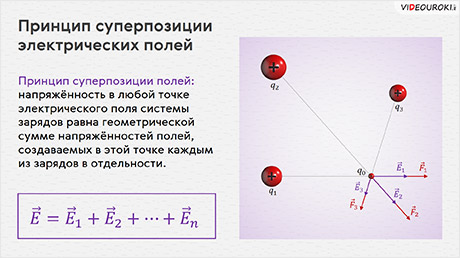
Принцип суперпозиции электрических полей.

Принцип суперпозиции (наложения) полей формулируется так:

Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых и т. д., то результирующая напряженность поля в этой точке равна: .

Принцип суперпозиции полей справедлив для случая, когда поля, созданные несколькими различными зарядами, не оказывают никакого влияния друг на друга, т. е. ведут себя так, как будто других полей нет. Опыт показывает, что для полей обычных интенсивностей, встречающихся в природе, это имеет место в действительности.

Благодаря принципу суперпозиции для нахождения напряжен­ности поля системы заряженных частиц в любой точке достаточно воспользоваться выражением напряженности поля точечного заряда.

На рисунке ниже показано, как в точке A определяется напряжен­ность поля , созданная двумя точечными зарядами q₁ и q₂.

Силовые линии электрического поля.

Электрическое поле в пространстве принято представлять силовыми линиями. Понятие о силовых линиях ввел М. Фарадей при исследовании магнетизма. Затем это понятие было развито Дж. Максвеллом в исследованиях по электромагнетизму.

Силовая линия, или линия напряженности электрического поля, — это линия, касательная к которой и каждой ее точке совпадает с направлением силы, действующей на положительный точечный заряд, находящийся в этой точке поля.

На рисунках ниже изображены линии напряженности положительно заряженного шарика (рис. 1); двух разноименно заряженных шариков (рис. 2); двух одноименно заряженных ша­риков (рис. 3) и двух пластин, заряженных разными по знаку, но одинаковыми по абсолютной величине зарядами (рис. 4).

Линии напряженности на последнем рисунке почти параллельны в пространстве между пластинами, и плотность их одинакова. Это говорит о том, что поле в этой области пространства одно­родно. Однородным называется электрическое поле, напряженность которого одинакова во всех точках пространства.

В электростатическом поле силовые линии не замкнуты, они всегда начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Они нигде не пересекаются, пересе­чение силовых линий говорило бы о неопределенности направления напряженности поля в точке пересечения. Плотность силовых линий больше вблизи заряженных тел, где напряженность поля больше.

Поле заряженного шара.

Напряженность поля заряженного про­водящего шара на расстоянии от центра шара, превышающем его радиус r ≥ R. определяется по той же формуле, что и поля точечного заряда . Об этом свидетельствует распределение силовых линий (рис. а), аналогичное распределению линий напряженности то­чечного заряда (рис. б).

Заряд шара распределен равномерно по его поверхности. Внутри проводящего шара напряженность поля равна нулю.

Источник

Электростатическое поле точечного заряда и заряженной сферы

теория по физике 🧲 электростатика

Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.

Электростатическое поле точечного заряда

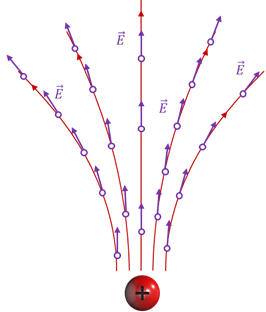
Направление силовых линий электростатического поля точечного заряда

Положительный заряд +Q	Отрицательный заряд –Q
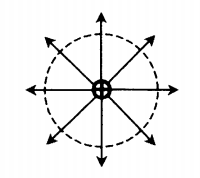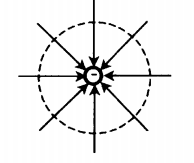У положительного заряда силовые линии направлены по радиальным линиям от заряда.	У отрицательного заряда силовые линии направлены по радиальным линиям к заряду.

Модуль напряженности не зависит от значения пробного заряда q₀:

Модуль напряженности точечного заряда в вакууме:

Модуль напряженности точечного заряда в среде:

Сила Кулона:

Потенциал не зависит от значения пробного заряда q₀:

Потенциал точечного заряда в вакууме:

Потенциал точечного заряда в среде:

Внимание! Знак потенциала зависит только от знака заряда, создающего поле.

Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.

Работа электрического поля по перемещению точечного заряда:

A 12 = ± q ( φ 1 − φ 2 )

Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз? Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:

Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.

Электростатическое поле заряженной сферы

Направление силовых линий электростатического поля заряженной сферы:

Положительно заряженная сфера +Q	Отрицательно заряженная сфера –Q
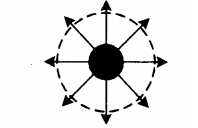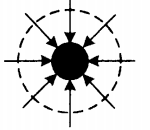У положительно заряженной сферы силовые линии — это радиальные линии, которые начинаются из этой сферы.	У отрицательно заряженной сферы силовые линии — это радиальные линии, которые заканчиваются в этой сфере.

Модуль напряженности электростатического поля заряженной сферы:

Сила Кулона:

Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.

Так как сфера заряжена положительно, то потенциал тоже положителен:

Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?

Алгоритм решения

Решение

Запишем исходные данные:

Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:

Закон Кулона для второй пары:

Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:

После изменения зарядов модуль силы взаимодействия между ними останется равным F.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В трёх вершинах квадрата размещены точечные заряды: +q, – «>– q, +q (q >0) (см. рисунок). Куда направлена кулоновская сила, действующая со стороны этих зарядов на точечный заряд +2q, находящийся в центре квадрата?

Алгоритм решения

Решение

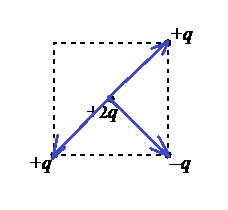
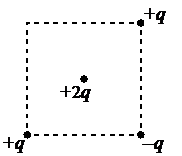
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:

Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.

Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).

pазбирался: Алиса Никитина | обсудить разбор | оценить

На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?

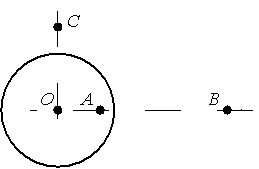
Установите соответствие между физическими величинами и их значениями.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Источник

Поле точечного заряда и заряженного шара. Принцип суперпозиции полей

Урок 44. Физика 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Поле точечного заряда и заряженного шара. Принцип суперпозиции полей»

Вам известно, что электрическое поле не действует на наши органы чувств, его невозможно увидеть. Но мы можем получить некоторое представление о распределении поля в пространстве. Для этого давайте изобразим векторы напряжённости поля, создаваемого неподвижным зарядом, в нескольких точках пространства.

Впервые этот способ изображения электрических полей в виде воображаемых линий, называемых линиями напряжённости (или силовыми линиями), был предложен в 1845 году Майклом Фарадеем.

Под линиями напряжённости мы с вами будем понимать воображаемые направленные линии, касательные к которым в каждой точке поля совпадают по направлению с напряжённостью электрического поля в той же точке.

Интересно, но сам Фарадей считал, что силовые линии существуют в действительности и похожи на растянутые упругие нити. Сейчас же мы точно знаем, что они не более реальны, чем земные меридианы и параллели, изображаемые на глобусах.

При построении линий напряжённости необходимо придерживаться следующих правил. Во-первых, касательная к линии напряжённости в каждой точке должна совпадать с направлением вектора напряжённости.

Во-вторых, следует помнить, что линии напряжённости электростатического поля — это незамкнутые линии: они начинаются на поверхности положительных зарядов и оканчиваются на поверхности отрицательных зарядов (или в бесконечности). В-третьих, линии напряжённости не должны пересекаться, так как в каждой точке поля вектор напряжённости имеет лишь одно направление.

И, наконец, чтобы линии напряжённости отображали не только направление, но и модуль напряжённости поля, на рисунках их условились проводить с определённой густотой: их рисуют гуще там, где модуль напряжённости поля больше, и реже — где он меньше.

На рисунке вы видите пример линий напряжённости двух пластин, заряды которых равны по модулю и противоположны по знаку.

Обратите внимание, что в пространстве между пластинами линии напряжённости практически параллельны друг другу (за исключением пространства вблизи краёв пластин и вне области их перекрытия) и находятся на равных расстояниях друг от друга: здесь электростатическое поле одинаково во всех точках. Так вот, если напряжённость поля одинакова во всех его точках, то такое поле называется однородным.

Теперь давайте посмотрим, как рассчитывается напряжённость электростатического поля, созданного точечным зарядом, модуль которого равен |Q|. Для этого поместим в некоторую точку поля положительный пробный заряд q₀.

Согласно закону Кулона, на пробный заряд со стороны поля будет действовать сила, модуль которой прямо пропорционален произведению модулей обоих зарядов и обратно пропорционален квадрату расстояния между зарядом, создающим поле, и точкой, в которую помещён пробный заряд:

Далее вспомним, что по определению, модуль напряжённости в данной точке поля равен отношению модуля силы, с которой поле действует на пробный заряд, находящийся в выбранной точке, к величине этого заряда:

Подставим выражение для модуля кулоновской силы в формулу для модуля напряжённости поля:

По полученной формуле мы с вами можем рассчитать напряжённость в любой точке поля, созданного неподвижным точечным зарядом.

Если же точечный заряд, создающий поле, находится в какой-либо проводящей среде, то в знаменатель формулы следует добавить множитель значения её диэлектрической проницаемости ε:

По этой же формуле можно рассчитывать напряжённость поля, образованного равномерно заряженным шаром в точках, которые находятся на его поверхности и вне его. Внутри же заряженного шара (или проводящей сферы), как мы увидим дальше, напряжённость поля равна нулю:

А теперь давайте подумаем, как найти напряжённость в некоторой точке поля, если оно создано не одним, а несколькими зарядами.

Очевидно, что если поместить в исследуемую точку такого поля пробный заряд, то на него будут действовать кулоновские силы со стороны каждого из зарядов в отдельности, создающих поле. Из механики мы знаем, что если на тело действует несколько сил, то результирующая сила равна их геометрической сумме. То же самое справедливо и для электрических сил:

Разделим записанное равенство на величину пробного заряда:

И учтём, что отношение силы, действующей на пробный заряд со стороны электрического поля, к величине этого заряда, есть напряжённость:

Последнее равенство выражает принцип суперпозиции полей: напряжённость в любой точке электрического поля системы зарядов равна геометрической сумме напряжённостей полей, создаваемых в этой точке каждым из зарядов в отдельности:

При этом напряжённость поля, создаваемого отдельным зарядом, определяется так, как будто других зарядов вокруг не существует.

А теперь для закрепления материала решим с вами несколько задач. Задача 1. Заряженный шарик радиусом 5 сантиметров находится в среде, диэлектрическая проницаемость которой равна 2. Найдите напряжённость поля в точке, удалённой от поверхности шарика на 3 сантиметра, если заряд шарика равен 3 пКл.

Задача 2. Электрическое поле создаётся двумя точечными зарядами 30 нКл и – 10 нКл, находящимися в вакууме на расстоянии 5 см друг от друга. Определите напряжённость поля в точке, находящейся на расстоянии 3 см от первого заряда и 4 см от второго.

Источник