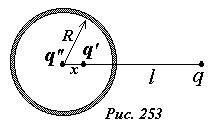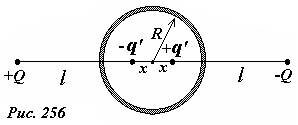поле точечного заряда вблизи проводящей плоскости

Точечный заряд у проводящей плоскости

В качестве простейшего применения этого метода используем плоскую эквипотенциальную поверхность В (см. фиг. 6.8). Она поможет нам решить задачу о заряде вблизи проводящей плоскости. Для этого зачеркнем просто левую часть фигуры. Линии поля нашего решения показаны на фиг. 6.10. Заметьте, что плоскость обладает нулевым потенциалом, потому что она находится как раз на полпути между зарядами. Мы решили задачу о положительном заряде вблизи заземленной проводящей плоскости.

Так мы узнали суммарное поле, но что можно сказать о том, каковы те реальные заряды, которые создали его? Кроме нашего положительного точечного заряда, ими являются какие-то отрицательные заряды, наведенные на проводящей плоскости и притянутые положительным зарядом (с каких-то далеких расстояний). Но теперь пусть вам захотелось узнать (то ли для технических целей, то ли просто из любопытства), как распределены эти отрицательные заряды по поверхности. Поверхностную плотность заряда вы сможете узнать, использовав результат, полученный в гл. 5, § 6 при помощи теоремы Гаусса. Нормальная составляющая электрического поля возле самого проводника равна плотности поверхностного заряда σ, деленной на ε₀. Мы можем узнать плотность заряда в каждой точке поверхности, отправляясь назад от нормальной составляющей электрического поля на поверхности. А ее мы знаем, потому что вообще нам известно поле в любой точке.

Рассмотрим точку поверхности на расстоянии ρ от той точки, которая расположена прямо против положительного заряда (см. фиг. 6.10). Электрическое поле в этой точке нормально к поверхности и направлено внутрь нее. Составляющая поля положительного точечного заряда, нормальная к поверхности, равна

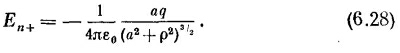К ней мы должны добавить электрическое поле, созданное отрицательным зеркальным зарядом. Это удвоит нормальную составляющую (и уничтожит все прочие), так что плотность заряда σ в произвольной точке поверхности будет равна

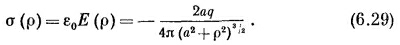Проинтегрировав σ по всей поверхности, мы сможем проверить наши расчеты. Мы должны получить весь наведенный заряд, т. е. —q.

Еще один вопрос: действует ли на точечный заряд сила? Да, потому что наведенные на плоскости отрицательные заряды должны его притягивать. А раз мы знаем, каковы эти поверхностные заряды [по формуле (6.29)], то можем с помощью интегрирования подсчитать силу, действующую на наш положительный заряд. Но мы ведь знаем также, что сила, действующая на него, в точности такая, какой она была бы, если бы вместо плоскости был один только отрицательный зеркальный заряд, потому что поля поблизости от них в обоих случаях одинаковы. Точечный заряд тем самым испытывает силу притяжения к плоскости, равную

Мы определили эту силу очень легко, без интегрирования по отрицательным зарядам.

Источник

Метод изображений в электростатике

Метод изображений в электростатике

Задачи о нахождении электрического поля системы нескольких точечных зарядов или системы зарядов, равномерно распределенным по каким-либо поверхностям, решаются в электростатике без особых сложностей. В самой худшей ситуации от Вас потребуется знание формулы Гаусса и, может быть, умение интегрировать. Решение этих задач существенно облегчено тем, что мы заранее знаем величины зарядов и то, как они распределены в пространстве.

Гораздо хуже дело обстоит в том случае, если мы имеем систему заданных точечных зарядов и каких-либо проводящих или диэлектрических поверхностей, расположенных вблизи них. Предположим, что мы хотим найти электрическое поле в такой задаче. Система зарядов вызовет перераспределение зарядов на поверхностях, в результате мы получим индуцированные заряды на поверхностях. Очевидно, что индуцированные заряды будут распределены по поверхностям неравномерно, особенно большая плотность заряда будет в тех точках поверхностей, которые расположены ближе всего к зарядам. Но как именно заряды распределены по поверхностям? Подобные задачи, как правило, не могут быть решены без использования численных методов, и такие расчеты проводят обычно на компьютерах.

Но есть достаточно большое количество частных случаев, в которых можно обойтись без использования вычислительной техники. Одним из методов решения таких задач является метод изображений, который заключается в сведении исходной задачи, в которой рассматриваются заряды и граничные поверхности, к задаче, в которой есть те же заряды и добавочные (фиктивные) заряды-изображения в безграничной среде. Эти заряды-изображения помещаются вне той области, в которой определяется поле. Правила построения зарядов-изображений полностью аналогичны тем, по которым строятся изображения точечных источников в оптике в системе зеркал. Зеркала имеют ту же форму, что и граничные поверхности. Величины зарядов-изображений определяются граничными условиями на поверхностях, а также требованиями одинаковости поля, создаваемого реальной системой зарядов и поверхностей, и системой, составленной из действительных зарядов и фиктивных зарядов-изображений в пространстве вблизи действительных зарядов.

В этой статье мы рассмотрим примеры использований метода изображений в электростатике.

Точечный заряд и проводящая плоскость

Пусть точечный заряд +q находится на расстоянии a от бесконечной проводящей, например, металлической плоскости с нулевым потенциалом (рис. 1 ). Какая сила действует на него?

Источник

§ 8. Точечный заряд у проводящей плоскости

В качестве простейшего применения этого метода используем плоскую эквипотенциальную поверхность В (см. фиг. 6.8). Она поможет нам решить задачу о заряде вблизи проводящей плоскости. Для этого зачеркнем просто левую часть фигуры. Линии поля нашего решения показаны на фиг. 6.10. Заметьте, что плоскость обладает нулевым потенциалом, потому что она находится как раз на полпути между зарядами. Мы решили за­дачу о положительном заряде вблизи заземленной проводящей плоскости.

Так мы узнали суммарное поле, но что можно сказать о том, каковы те реальные заряды, которые создали его? Кроме нашего положительного точечного заряда, ими являются какие-то отри­цательные заряды, наведенные на проводящей плоскости и при­тянутые положительным зарядом (с каких-то далеких расстоя­ний). Но теперь пусть вам захотелось узнать (то ли для техни­ческих целей, то ли просто из любопытства), как распределены эти отрицательные заряды по поверхности. Поверхностную плотность заряда вы сможете узнать, использовав результат, полученный в гл. 5, § 6 при помощи теоремы Гаусса. Нормаль­ная составляющая электрического поля возле самого провод­ника равна плотности поверхностного заряда а, деленной на ₀. Мы можем узнать плотность заряда в каждой точке поверхности, отправляясь назад от нормальной составляющей электриче­ского поля на поверхности. А ее мы знаем, потому что вообще нам известно поле в любой точке.

Фиг. 6.10. Поле заряда, помещенного близ плоской проводящей поверхности, найденное методом изображений.

Рассмотрим точку поверхности на расстоянии от той точки, которая расположена прямо против положительного заряда (см. фиг. 6.10). Электрическое поле в этой точке нор­мально к поверхности и направлено внутрь нее. Составляющая поля положительного точечного заряда, нормальная к поверх­ности, равна

Кней мы должны добавить электрическое поле, созданное отри­цательным зеркальным зарядом. Это удвоит нормальную со­ставляющую (и уничтожит все прочие), так что плотность за­ряда 0 в произвольной точке поверхности будет равна

Еще один вопрос: действует ли на точечный заряд сила? Да, потому что наведенные на плоскости отрицательные заряды должны его притягивать. А раз мы знаем, каковы эти поверх­ностные заряды [по формуле (6.29)], то можем с помощью интег­рирования подсчитать силу, действующую на наш положитель­ный заряд. Но мы ведь знаем также, что сила, действующая на него, в точности такая, какой она была бы, если бы вместо плоскости был один только отрицательный зеркальный заряд, потому что поля поблизости от них в обоих случаях одинаковы. Точечный заряд тем самым испытывает силу притяжения к пло­скости, равную

Мы определили эту силу очень легко, без интегрирования по отрицательным зарядам.

§ 9. Точечный заряд у проводящей сферы

А какие еще поверхности, кроме плоскости, имеют простое решение? Самая простая из них — сфера. Попробуем определить поля вокруг металлической сферы с точечным зарядом q вблизи нее (фиг. 6.11). Придется поискать простую физическую задачу, для которой сфера есть эквипотенциальная поверхность. Если мы просмотрим те задачи, которые уже решены, то увидим, что у поля двух неравных точечных зарядов одна из эквипотен­циальных поверхностей как раз и есть сфера. Отметим себе это! Если мы как следует подберем положение заряда-изображения и нужную его величину, может быть, тогда мы и сможем подо­гнать эквипотенциальную поверхность к нашей сфере.

Фиг. 6.11. Точечный заряд q наводит на за­земленной проводящей сфере заряды, которые создают поле, такое же, как у заряда-изображе­ния, помещенного в ука­занной точке.

Это и впрямь может быть сделано, если действовать по следующему рецепту.

Положим, что вы хотите, чтобы эквипотенциальная поверх­ность была сферой радиуса а с центром, отстоящим от заряда q на расстояние b. Поместите изображение заряда величины q’=-q(a/b) на радиусе, проходящем через заряд на расстоянии a 2 /b от центра. Потенциал сферы пусть будет нуль.

Математически причина состоит в том, что сфера есть гео­метрическое место точек, отношение расстояний которых от двух данных точек постоянно. Как следует из фиг. 6.11, потен­циал в точке Р от зарядов q и q’ пропорционален сумме

ибудет равен нулю во всех точках, для которых

Если мы помещаем q’ на расстоянииа 2 !b от центра, то отноше­ниеr₂/r₁равно постоянной величинеa/b. Тогда если

то сфера станет эквипотенциалью. Потенциал ее на самом деле будет равен нулю.

Ачто, если нам понадобится сфера с ненулевым потенциалом? Ведь он равен нулю только тогда, когда ее суммарный заряд слу­чайно окажется равнымq’! Конечно, если ее заземлить, то наведенные на ней заряды окажутся в точности такими, как на­до. Ну, а если она заизолирована и мы не снабдили ее никаким зарядом? Или снабдили ее зарядом Qq’? Или она находится под напряжением, не равным нулю? Такие вопросы разрешаются сходу. Всегда ведь можно добавить в центр сферы точечный заряд q». По принципу наложения сфера всегда останется эк­випотенциальной, а изменится только величина потенциала. Если у нас, скажем, есть проводящая сфера, предваритель­но разряженная и изолированная от всего, и мы поднесли к ней положительный заряд q, то суммарный заряд сферы останется равным нулю. Решение можно найти, взяв тот же, что и прежде, заряд-изображение q’ и вдобавок к нему заряд в центре сферы, такой, что

Поля повсюду вне сферы будут получаться наложением полей от q, q’ и q«. Задача решена.

Теперь ясно, что между сферой и точечным зарядом q долж­на существовать сила притяжения. Она не пропадает, даже если сфера нейтральна, на ней нет никакого заряда. Откуда же берется притяжение? Когда вы подносите к проводящей сфере положительный заряд, то он притягивает отрицательные за­ряды на ближний конец сферы, положительные же оставляет на дальнем. А притяжение отрицательными зарядами пере­вешивает отталкивание положительными; в итоге остается при­тяжение. Силу его можно прикинуть, подсчитав силу, действую­щую на q в поле, созданном q’ и q«. Суммарная сила равна силе притяжения между зарядами q и q’ = -(a/b)q на расстоянии b-(а 2 /b) плюс сила отталкивания q и заряда q» = +(a/b)q на расстоянии b.

Источник

Учебники

Журнал «Квант»

Общие

§10. Проводники и диэлектрики в электростатическом поле

10.4 Расчет поля в присутствии проводников. Метод изображений.

Мы уже подчеркивали, что основная проблема расчета полей в присутствии проводников заключается в появлении индуцированных зарядов, распределение которых заранее не известно. В связи с этим рассмотренные ранее методы, основанные на законе Кулона и принципе суперпозиции, в данном случае оказываются непригодными. Принципиально иной подход к решению данной задачи заключается в расчете распределения потенциала электростатического поля. Действительно, на поверхности проводника распределение заряда не известно, но ведь потенциал проводника постоянен!

Сам метод основан на решении уравнений [1] для потенциала поля. Сами эти уравнения довольно сложны и рассматриваются в курсе физики высшей школы, однако, их физический смысл основывается на законе Кулона и связи потенциала с напряженностью поля.

Однако в некоторых случаях можно рассчитать электрическое поле и распределение индуцированных на поверхности проводника зарядов, используя искусственный прием, который называется метод изображений.

Изложим кратко суть и дадим обоснование этого метода.

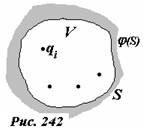
Пусть в некоторой области пространства V, ограниченной поверхностью S (в частном случае граница области может простираться до бесконечности), задано распределение зарядов q_i (рис. 242).

Электрическое поле в выделенной области определяется однозначно, если

Заметим, что на границе области могут существовать заряды, однако даже при неизвестном их распределении, задание потенциала на границе однозначно определяет поле внутри области. Поэтому две различные задачи, но с одинаковыми распределениями зарядов внутри области и одинаковыми потенциалами на границе имеют внутри области одинаковые решения. Иногда при неизвестном распределении индуцированных зарядов на границе удается подобрать такое распределение зарядов вне рассматриваемой области, что для нового распределения выполненяются граничные условия исходной задачи. В этом случае дополнительные заряды называются зарядами-изображениями. Поиск изображений имеет смысл вести тогда, когда новая задача оказывается проще исходной и имеет простое решение.

Помимо задания распределения потенциала, в качестве граничных условий могут использоваться и некоторые другие, например, значение напряженности поля. Формулировке граничных условий, по этой причине уделяется серьезное внимание в курсе электродинамики.

Точечный заряд над плоской проводящей поверхностью.

Рассмотрим простейшую задачу, допускающую решение с помощью метода изображений.

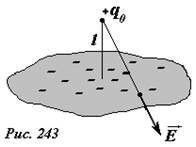
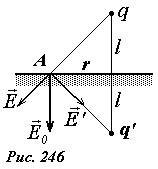
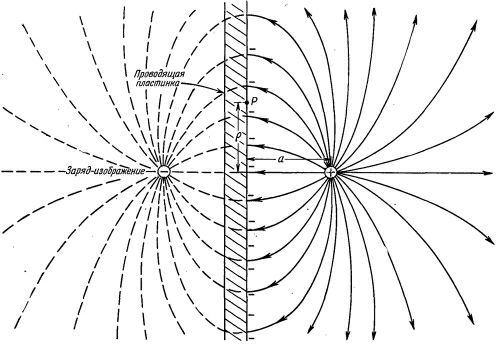
Пусть точечный заряд +q₀ находится на расстоянии l от бесконечной металлической пластины (рис. 243).

Очередной раз мы пользуемся моделями – в данном случае под бесконечной, понимается пластина, размеры которой значительно больше расстояния до заряда. Кроме того, можно считать, что пластина заземлена, так как она «касается бесконечности».

Под действием электрического поля заряда +q₀ электроны пластины придут в движения и начнут скапливаться под точечным зарядом, создавая отрицательный индуцированный заряд.

Если пластина реально заземлена, то эти заряды натекут из заземления. На большой незаземленной пластине возникнут положительные заряды на краях пластины, но так как эти края находятся далеко, то их полем в рассматриваемой области можно пренебречь.

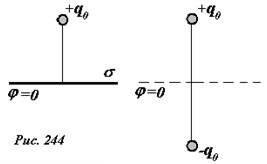
Распределение поверхностной плотности индуцированных зарядов на пластине σ не известно, но известно, что ее потенциал постоянен и равен нулю.

Сравним данную простую задачу (два точечных заряда) с исходной (точечный заряд и индуцированные им заряды σ на проводящей пластине): в полупространстве над пластиной распределения зарядов одинаковы (в обоих случаях – один точечный заряд), на граничной плоскости потенциалы равны; следовательно, в этом полупространстве электрические поля также одинаковы.

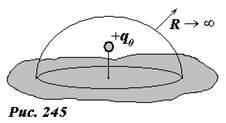
Строго говоря, мы должны рассматривать замкнутую область пространства, поэтому мысленно накроем заряд +q₀ полусферой, опирающейся на плоскость, положим ее потенциал равным нулю и устремим ее радиус к бесконечности, и таким образом придем к рассматриваемому полупространству (рис. 245).

Напряженность суммарного поля у границы \(

\vec E_0\) можно рассчитать по принципу суперпозиции как сумму полей, создаваемых исходным зарядом \(

\vec E\)и его изображением \(

Суммарный вектор направлен перпендикулярно границе и равен

Сила притяжения заряда к пластине определяется полем, создаваемым индуцированными зарядами, которое в свою очередь эквивалентно полю заряда изображения, поэтому равно силе взаимодействия двух точечных зарядов q и q’

Этот вывод можно пояснить следующим образом: при двух реальных точечных зарядах при перемещении одного из них второй остается неподвижным. Если же уносить заряд от проводящей границы, то его изображение также удаляется, поэтому совершаемая работа будет меньше.

Картина силовых линий также может быть рассчитана, как поле двух точечных зарядов (рис. 247). Обратите внимание, что во всех точках плоскости силовые линии перпендикулярны поверхности.

Продолжим развитие идей построения зарядов-изображений.

Совершенно аналогично можно построить поле заряда, помещенного на биссектрису двугранного угла, величина которого целое число раз укладывается в полном угле, например, в угле 60°. Шесть зарядов, знаки которых чередуются, расположенных в вершинах правильного шестиугольника, обеспечивают равенство нулю потенциала на гранях угла.

Изображение заряда в сфере.

Прежде, чем приступить к рассмотрению следующей группы задач, связанных с описанием взаимодействия точечного заряда и проводящей сферы, решим одну вспомогательную задачу.

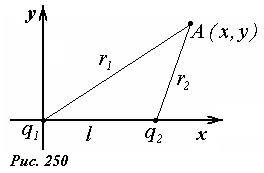
Пусть электростатическое поле создается двумя точечными зарядами, находящимися на расстоянии l друг от друга. Величины и знаки зарядов различны и равны q₁ и q₂. Покажем, что поверхность нулевого потенциала этого поля представляет собой сферу.

Выберем систему координат, так чтобы заряд q₁ находился в начале координат, а заряд q₂ на оси Ox (рис. 250). Так задача обладает осевой симметрией, то достаточно показать, что в плоскости xOy линия нулевого потенциала является окружностью. Запишем выражение для потенциала электростатического поля в произвольной точке A с координатами (x,y)

Полагая φ = 0, получим уравнение, определяющее линию нулевого потенциала. Обозначим \(

А это есть уравнение окружности радиуса \(

Итак, запомним – в поле создаваемом двумя точечными зарядами разными по знаку и величине, поверхность нулевого потенциала представляет собой сферу.

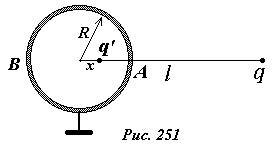
Рассмотрим теперь такую систему: точечный заряд q расположен на расстоянии l от центра металлической заземленной сферы радиуса R. Исследуем электрическое поле в этом случае.

На поверхности металлической заземленной сферы возникнут индуцированные заряды, распределение которых заранее не известно, однако потенциал сферы равен нулю. Мы показали, что поле двух точечных зарядов имеет в качестве поверхности нулевого потенциала сферу. Теперь мы можем использовать этот результат.

Для определения величины заряда-изображения q’ и его положения можно потребовать выполнения условия φ = 0 в двух точках сферы, например, A и B (рис. 251):

Решив эту систему относительно неизвестных q’ и x, получим

Для определения суммарного индуцированного заряда воспользуемся теоремой Гаусса. Окружим сферу замкнутой поверхностью. По теореме Гаусса, поток вектора напряженности электрического поля через эту поверхность равен суммарному заряду внутри поверхности, деленному на ε₀. Так поле индуцированных зарядов эквивалентно полю заряда изображения, то и суммарный индуцированный заряд равен величине заряда-изображения \(

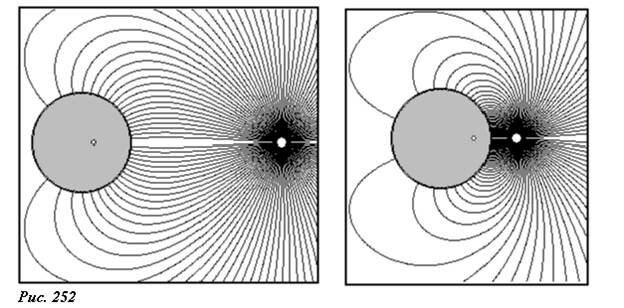
На рисунке 252 показаны силовые линии поля, при двух различных значениях расстояниях до точечного заряда. Обратите внимание, что при увеличении расстояния между зарядом и сферой искажения поля точечного заряда уменьшаются. Как всегда, у поверхности проводника силовые линии перпендикулярны границе, что соответствует условию равновесия индуцированных зарядов на поверхности проводника.

Силу взаимодействия между сферой и точечным зарядом можно найти как силу взаимодействия между двумя точечными зарядами q, q’ :

Заметим, что при l >> R сила взаимодействия становится равной

Итак, вне сферы поле, создаваемое точечным зарядом q и индуцированными зарядами на поверхности, эквивалентно полю трех точечных зарядов q, q’, q’’.

Обратите внимание, число зарядов изображений определяется только необходимостью выполнения граничных условий.

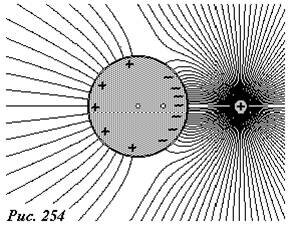
На рисунке 254 показана картина силовых линий электрического поля рассматриваемой системы зарядов. Обратите внимание, что имеются силовые линии, начинающиеся на положительных зарядах сферы. Незаземленная сфера гораздо меньше возмущает поле точечного заряда, чем заземленная. Действительно, на ней происходит только перераспределение зарядов.

Сила, действующая на заряд q, вычисляется как сумма сил, действующих со стороны двух изображений

При l >> R сила взаимодействия

убывает обратно пропорционально пятой степени расстояния, что также легко объяснимо: величина индуцированного дипольного момента пропорциональна величине внешнего поля (которое убывает обратно пропорционально квадрату расстояния), а величина поля диполя убывает обратно пропорционально кубу расстояния.

Заметим, что в данном случае можно вычислить потенциал сферы, не рассчитывая распределения зарядов на поверхности. По принципу суперпозиции, потенциал центра сферы равен сумме потенциалов заряда q и индуцированных зарядов на поверхности сферы. Все индуцированные заряды находятся на одном и том же расстоянии от центра и их сумма равна нулю, следовательно, равен нулю и потенциал, создаваемый ими в центре сферы. Поэтому потенциал в центре сферы, следовательно, и в любой ее точке, равен потенциалу поля точечного заряда \(

Суммарный заряд сферы остается равным нулю, но сфера приобретает индуцированный дипольный момент, который равен дипольному моменту двух зарядов-изображений

Перепишем эту формулу в виде

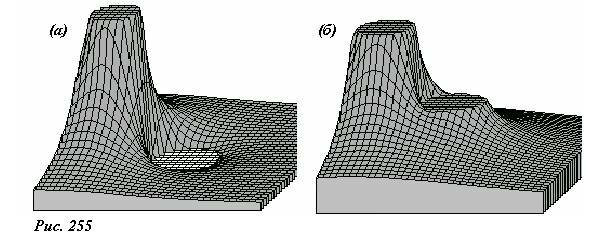
Достаточно интересно рассмотреть распределение потенциала в плоскости, проходящей через точечный заряд и центр сферы. Эти потенциальные функции для заземленной (а) и незаземленной (б) сфер изображены на рисунке 255. Функция, описывающая потенциал поля, вне сферы совпадает с потенциалом поля точечных зарядов (исходного и изображений), а внутри сферы равна нулю в случае (а) и постоянна в случае (б) – круглые горизонтальные площадки совпадает с сечением сферы. Резкое «возвышение» есть потенциал поля точечного заряда, который стремится к бесконечности, здесь, как и на других рисунках, он «обрезан».

Проводящий шар в однородном поле.

x = \frac\) от центра шара. Теперь мысленно начнем уносить заряды Q на бесконечность \(

При увеличении расстояния между зарядами поле в области шара становится практически однородным с напряженностью

Выразим индуцированный дипольный момент шара через напряженность поля

как видите, этот дипольный момент не зависит от «придуманных» зарядов Q и расстояния l, поэтому и в однородном поле шар будет иметь такой же дипольный момент. Обратите внимание, что и в данном случае поляризуемость шара равна его утроенному объему.

Таким образом, поле индуцированных на поверхности шара зарядов эквивалентно полю точечного диполя, находящегося в центре шара. Картину силовых линий такого поля мы уже использовали ранее.

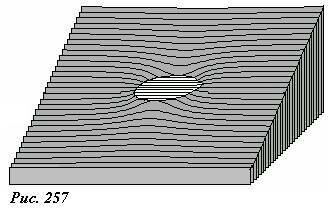
Неплохо также смотрится и распределение потенциала (рис. 257).

Заметим, что потенциал однородного поля изменяется по линейному закону, поэтому распределение потенциала в таком поле изображается наклонной плоскостью. При помещении в это поле проводящего шара на наклонной плоскости появляется горизонтальная площадка, постоянного потенциала на проводнике.

Задание для самостоятельной работы.

Источник