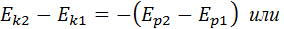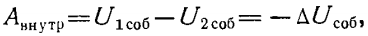потенциальная энергия частицы в поле консервативных сил

Беседа 2. Потенциальная энергия

Коллега, о потенциальной энергии, пожалуйста, поподробнее.

Вы, мой друг, совершенно правильно интересуетесь важнейшей составляющей полной энергии.

Принято считать, что потенциальная энергия является частью общей энергии системы, зависящей от взаимного расположения материальных частиц, составляющих эту систему, и от их положений во внешнем силовом поле (гравитационное, электрическое поле).

Силовым полем мы называем ту часть пространства, в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила.

Численно потенциальная энергия системы в данном её положении равна работе, которую произведут действующие на систему силы при её перемещении из этого положения в то, где потенциальная энергия равна нулю.

Коллега, энергией обладает только пробное тело в потенциальном поле или потенциальное поле тоже?

Для ответа на Ваш вопрос открываем БСЭ (Большая Советская Энциклопедия) и в разделе «Поля физические» читаем (дословно):
«Поля физические, особая форма материи; физическая система, обладающая бесконечно большим числом степеней свободы. Примерами полей физических могут служить электромагнитное и гравитационное поля. ».

Отсюда следует, что потенциальное поле является материальной средой. Значит, как и любая материальная среда, это поле обладает энергией (соответственно, и массой). Кстати, это подтверждается, к примеру, наличием в поле электромагнитных волн, которые являются колебаниями этой материальной среды.

Конкретные границы поля определить сложно, поэтому физики давно привыкли оперировать энергией, содержащейся в единице объёма, то есть – объёмной плотностью энергии потенциального поля (измеряется в Дж/м 3 ). Возьмём, к примеру, книгу Зильбермана «Электричество и магнетизм» (Наука, М., 1970) и на стр. 136 читаем (дословно):
«В плоском конденсаторе и вообще в однородном поле плотность энергии, т. е. энергия, содержащаяся в единице объёма, постоянна и равна полной энергии, делённой на объём».

Коллега, раз уж потенциальное поле является материальной средой, то оно должно характеризоваться конкретными параметрами, которые можно вычислить и измерить.

Вы совершенно правы. Мы уже выяснили, что электрическое (потенциальное) поле характеризуется таким параметром, как объёмная плотность энергии (далее – давление, Дж/м 3 или Н/м 2 ). Кроме этого, потенциальное поле характеризуется потенциалом и его градиентом – напряженностью поля. Причем, давление, потенциал и напряженность характеризуют потенциальное поле в данной его точке, независимо от наличия в этой точке пробного тела, ибо поле, как мы уже знаем, само обладает энергией и массой.

Если потенциальную энергию (W_П, Дж) отнести к единичной массе (m, кг) или к единичному электрическому заряду (q, Кл), то получим гравитационный (v 2 = W_П/m, Дж/кг) или электрический (U = W_П/q, Дж/Кл) потенциалы.

Градиентом потенциала в данной его точке является напряженность поля:
— для гравитационного поля: g = – grad v 2 ;
— для электрического: E = – grad U (о знаке речь пойдет ниже).

Градиент (от лат. gradiens, род. падеж gradientis – шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины от одной точки пространства к другой.

С удалением от центра поля изменяется не только потенциал, но и потенциальная энергия. И её градиентом является сила, которую мы называем силой тяготения.

Уравнение F = – grad W_П показывает, что работа сил вдоль замкнутой траектории в потенциальном поле всегда равна нулю.

Коллега, какие единицы измерения наиболее приемлемы для вышеназванных параметров?

Очень хороший вопрос. СИЛА измеряется в ньютонах (Н = кг*м/с 2 ) или в Дж/м. Второй вариант записи более приемлемый, ибо сразу даёт нам указание на то, что сила является всего лишь ГРАДИЕНТОМ ЭНЕРГИИ (Дж/м). Это важно, ибо упрощает дальнейшее понимание физических процессов. Кстати, это касается не только силы, но и таких параметров, как давление и потенциал.

ПОТЕНЦИАЛ измеряется в м 2 /с 2 или в Дж/кг (для гравитационного поля) и в (кг/Кл)*( м 2 /с 2 ) или Дж/Кл (для электрического поля). И здесь более приемлемым является второй вариант записи, ибо сразу указывает на значение потенциальной энергии, отнесенной к единице массы (Дж/кг) для гравитационного поля или отнесенной к единице электрического заряда (Дж/Кл) для электрического поля.

И наконец, коллега, давайте рассмотрим, как определяется значение потенциальной энергии.

Пожалуй, теперь мы готовы решать и эту проблему. Значение потенциальной энергии определяется двумя способами:
— упрощенный (приближенный) – для однородного поля;
— общий (истинный) – для неоднородного поля, которое нас реально и окружает.

Потенциальное поле можно условно считать однородным, если вектор напряженности во всех его точках имеет одно и то же значение и направление. К примеру, для гравитационного поля это правило можно применить только у поверхности Земли на небольшом её участке (скажем, в лабораторном опыте). В этом случае для упрощения расчетов значение потенциальной энергии пробного тела на поверхности Земли условно принимается равной нулю, а её значение в любой другой точке определяется из уравнения:

W_П = mgh, Дж,
где g – напряженность гравитационного поля (Н/кг), а h – вертикальное расстояние (м) от поверхности Земли до пробного тела массой m (кг).

Здесь знак перед значением потенциальной энергии принципиального значения не имеет.

Коллега, но ведь это и есть наиболее распространенный способ определения потенциальной энергии.

К сожалению, многие учебники физики на этом и завершают определение потенциальной энергии. Но не все. Взять, к примеру, Общий курс физики Сивухина (Москва, МФТИ, 2005) или американский курс Физики в переводе под редакцией Ахматова (Москва, Наука, 1974).

Здесь рассматривается:
— уже известный нам способ определения потенциальной энергии пробного тела в однородном поле тяжести у поверхности Земли (том 1, стр. 144-145 первого источника и часть III, стр.152-157 второго источника);
— и общий способ определения потенциальной энергии для неоднородного поля (том 1, стр. 145-146 первого источника и часть III, стр.157-159 второго источника).

Общий способ расчета дает уже отрицательное значение потенциальной энергии:
— уравнение (25.6) W(U) = – GMm/r в первом источнике и
— уравнение W(Ur) = – GMm/r – во втором.

Отрицательное значение потенциальной энергии здесь объясняется следующим образом:
— в первом источнике (цитата): «Максимальной энергией притягивающиеся массы обладают при бесконечном расстоянии между ними. В этом положении потенциальная энергия считается равной нулю. Во всяком другом положении она меньше, т. е. отрицательна»;
— во втором источнике дано доказательство правильности уравнения W(Ur) = – GMm/r.

И действительно, свободно падающее к центру поля тело теряет свою потенциальную энергию, которая переходит в кинетическую. Значит, потенциальная энергия с уменьшением расстояния между центрами масс (M и m) уменьшается и, наоборот, с увеличением расстояния – увеличивается.

Учитывая, что в уже известном нам уравнении W_П = – GMm/r символ радиуса находится в знаменателе, то предельно ясно, что с увеличением расстояния (значение радиуса стремится к бесконечности) потенциальная энергия увеличивается до… нуля. Такое возможно только в том случае, если потенциальная энергия во всяком другом положении отрицательна.

Вывод: потенциальная энергия для всех материальных частиц отрицательна.

Отсюда следует, что значение гравитационного потенциала v 2 = W_П/m = – GM/r тоже отрицательно. И подтверждением этому является уравнение (3) в разделе «Тяготение» (стр. 772) Физического Энциклопедического Словаря или аналогичного раздела Большой Советской Энциклопедии.

Аналогично определяется значение потенциальной энергии и электрического потенциала в электрическом поле. Причем далее мы убедимся в том, что потенциальная энергия и её объёмная плотность (давление) ОДИНАКОВЫ и для гравитационного, и для электрического полей.

Коллега, теперь попробуйте записать Ваше высказывание в виде формулы.

Формулы пишут математики, а физики пользуются уравнениями. Необходимые уравнения здесь уже приводились. Однако попробуем, все же, обойтись пока без них, тем более – без «формул».

Для этого используем бытовые наблюдения, которые подсказывают: чтобы испарить воду, кипящую в чайнике, нужно сжечь некоторое количество дров или газа. Другими словами, нужно совершить работу. С помощью термометра можно убедиться, что температура кипящей воды и температура пара над ней одинаковы. Следовательно, одинакова и средняя энергия движения частиц в кипящей воде и в паре.

Вывод: тепловая энергия, передаваемая кипящей воде от топлива, преобразуется в энергию взаимодействия частиц испаряющейся воды. Значит, энергия связи частиц в кипящей воде меньше, чем в водяном паре. Но в паре эта энергия практически равна нулю, следовательно, энергия взаимодействия частиц в жидкости меньше нуля, т.е. отрицательна.

Коллега, Ваши доводы убедительны и примеры Вы приводите неопровержимые. Однако не все думают так же.

Однако математики так не думают. Для них гравитационное поле является ОДНОРОДНЫМ с неизменной напряженностью гравитационного поля (вроде этот параметр и не зависит от радиуса). Значение потенциальной энергии они определяют по упрощенной формуле W = mgh. Они не связывают h с радиусом поля, а считают его простым отрезком между двумя произвольными точками этого поля. Поэтому для них потенциальная энергия может принимать нулевое значение в любой понравившейся им точке. Нонсенс, но бывает и такое.

Но есть ещё и «физико-математики». Их мнение зависит от того, насколько они физики или математики.

Коллега, почему Вы считаете, что математики «тяготеют» к однородному полю?

В подтверждение этому открываем Краткий курс математического анализа (Бермант, Араманович, 2005) и на стр. 520 в разделе «Теория поля» читаем:
«Векторное поле называется однородным, если А(Р) — постоянный вектор, т.е. Ах, Аy и Az — постоянные величины.
Примером однородного поля может служить, например, поле тяжести».

Теперь Вы и сами видите, что математики гравитационное поле называют «полем тяжести» и «всерьёз» считают его однородным. И это не просто безобидное заблуждение, ибо оно мешает нам осознать Природу гравитации. Однако, об этом мы поговорим немного позже.

Источник

Потенциальная энергия частицы в поле.

В стационарном поле работа консервативных сил зависит только от начального и конечного положения частицы. Представим такое поле, где частица перемещается от разных точек Pi в точку О. Работа сил не зависит от пути, поэтому зависит только от положения точки Р. à Работа будет некоторой ф-ей радиус-вектора r точки Р. Эта ф-я будет обозначатся как U(r):

Найдем работу при перемещении точки из 1 в 2. Т.к. она не зависит от пути, то выберем путь через точку О, тогда:

или

Выражение справа (U₁-U₂) есть убыль потенциальной энергии или разность значение Еп в начальной и конечной точках пути. Таким образом, работа сил на пути 1-2 равна убыли потенциальной энергии.

Связь между потенциальной энергией и силой.

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы F, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии Eп.

Для установления связи вычислим элементарную работу dA, совершаемую силами поля при малом перемещении dr тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой r. Эта работа равна

где F- проекция силы на направление r. Поскольку в данном случае работа совершается за счет запаса потенциальной энергии Eп, она равна разности потенциальной энергии –dЕп на отрезке оси. А отсюда получаем:

Если разложить F по осям, то:

В векторном виде сила равна (grad – градиент):

Градиент – вектор, показывающий направление наибыстрейшего увеличения ф-и. “-“ показывает то, что вектор F направлен в сторону наибыстрейшего уменьшения Eп.

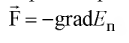
à Консервативная сила равна отрицательному градиенту Eп:

Билет 15

Полная механическая энергия частицы – энергия механического движения и взаимодействия, равная сумме кинетической и потенциальной энергий: E = Ek + Ep.

Приращение Ек или Т равно элементарно работе результирующей F_рез всех сил. В стационарном поле это консервативная сила этого поля F_конс и иные силы F_стор. à F_рез = F_конс + F_стор. Робота этих сил идет на приращение кинетической энергии частицы:

Отсюда видно, что работа сторонних сил идет на приращение величины T+U, что и есть полная механическая энергия.

Закон сохранения.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Билет 16

Теорема о кинетической энергии системы— одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел.

Кинетической энергией системы называют сумму кинетических энергий всех тел, входящих в систему. Для определённой таким образом величины справедливо утверждение:

Изменение кинетической энергии системы равно работе всех внутренних и внешних сил, действующих на тела системы.

Рассмотрим систему материальных точек с массами m_i, скоростями v_i и кинетическими энергиями Ti=1/2(m_iv_i 2 ). Для малого изменения кинетической энергии (дифференциала), происходящего в течение некоторого малого промежутка времени dt будет выполняться:

Используя второй закон Ньютона и обозначая равнодействующую всех сил, действующих на точку, как F_i получаем:

, F_ids_i есть работа А à

Суммирование всех уравнений такого вида, записанных для каждой из материальных точек, приводит к формуле для изменения полной кинетической энергии системы:

Данное равенство выражает утверждение теоремы об изменении кинетической энергии системы в дифференциальном виде.

Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени получим выражение теоремы об изменении кинетической энергии в интегральной форме:

где T₂ и Т₁ — значения кинетической энергии системы в моменты времени t₂ и t₁ cсоответственно.

Необходимо подчеркнуть, что здесь, в отличие от случаев теоремы об изменении количества движения системы и теоремы о движении центра масс системы, учитывается действие не только внешних, но внутренних сил.

Собственная потенциальная энергия системы— механическая энергия системы тел, которая определяется характером сил взаимодействия между телами этой системы и их взаимным расположением.

Рассмотрим систему, между частицами которой действуют лишь центральные силы. Центральные силы – силы, зависящие от расстояния между частицами и направленные по прямой, проходящий через эти частицы (граф. инт. в Вопросе 11).

Сначала возьмем систему из двух частиц. Работа в К-системе отсчета за время dt будет выглядеть как:

Согласно Третьему закону Ньютона F₂=-F₁, тогда:

Величина в скобках представляет собой перемещение частицы 1 относительно частицы 2. Вспомним принцип относительности Галилея (вопрос 8), тогда частица 1 перемещается в K’ системе, которая жестко связана с частицей два и перемещается вместе с ней относительно исходной системы K. à dr₁ = dr₂+dr’_1, dr1-dr2=dr’1 и:

ß Алгебраическая сумма элементарных работ пары сил взаимодействия в произвольной К-системе оказывается равной элементарной работе, которую совершает сила, действующая на одну частицу, в к системе отсчета, где другая покоится. à А_1,2 не зависит от выбранной системы отсчета.
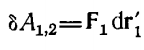
F1 действующая на частицу 1 со стороны частицы 2 центральная, а значит консервативная. Поэтому является убылью потенциальной энергии 1 в поле частицы 2 или как:

Рассмотрим систему из 3-ех частиц. По тому же принципу:

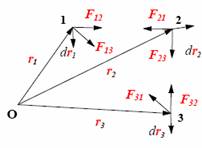
Данное утверждение абсолютно для любого числа частиц, поэтому каждой конфигурации системы частиц присуще свое значение Еп_собст и работа всех внутренних центральных сил при изменении конфигурации есть убыль Еп_собст:

Преобразуем представив каждое слагаемое в виде (Uik = U_ik+U_ki)/2 т.к U_ik=U_ki, тогда:

, а после группировки по индексам

, что есть ничто иное как

, а в общем виде

Классификация сил. По характеру взаимодействия:

Массовые (объёмные) силы обусловлены взаимодействием материальных тел на расстоянии, они приложены к каждой точке тела (распределены по всему его объёму). К массовым силам относятся силы гравитационного и электромагнитного взаимодействия. Обычно из чисто формальных соображений к ним добавляют силы инерции (для сил инерции невозможно указать конкретный материальный источник).

Поверхностные силы приложены к участкам поверхности и являются результатом взаимодействия материальных тел при непосредственном контакте. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные силы подразделяются на сосредоточенные и распределённые. К первым относятся нагрузки, площадь приложения которых несоизмеримо меньше площади поверхности тела. Таковыми являются, например, сила нормального давления P и сила трения T между колесом тележки и подкрановой балки, а также силы взаимодействия балки с опорами.

Билет 17

Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. (Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v).

Если инерциальная система отсчёта K’ движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид

y = y’, z = z’,

Рис. Система координат K’ движется относительно неподвижной системы координат K со скоростью v вдоль оси x.

Источник

Потенциальная энергия частицы в поле. Энергия упругой деформации. Связь между потенциальной энергией и силой поля

Рассмотрим стационарное поле консервативных сил. Работу консервативной силы можно представить как изменение (убыль) некоторой скалярной функции Е_р(г), зависящей только от положения частицы (тела), которая называется потенциальной энергией частицы:

Тогда работа сил поля при перемещении частицы из точки 1 в точку 2 может быть представлена как убыль потенциальной энергии Е_р(г) частицы в данном поле:

Из формулы (4.17) следует, что потенциальная энергия определена с точностью до произвольной постоянной. Поскольку в физических явлениях природы рассматривается не сама величина потенциальной энергии, а только ее изменение, то роль константы несущественна. Начало отсчета потенциальной энергии (Е = 0) выбирается из соображений удобства.

Единица потенциальной энергии в СИ — джоуль (Дж): 1 Дж = 1 Н м.

Определим энергию упругой деформации стержня. Внешние силы подчиняются закону Гука (3.21). Потенциальная энергия упруго растянутого (сжатого) стержня Е_р равна минимальной работе, совершаемой внешними силами при деформации, т.е. при 7 г _внеш = F:

Пусть х — удлинение стержня, которое изменяется в процессе деформации от 0 до А/. Тогда, согласно закону Гука (3.17), получаем для энергии упругой деформации Е, что потенциальная энергия упруго растянутого стержня пропорциональна квадрату деформации:

В ньютоновской механике широко используются два способа описания взаимодействия частицы с окружающими телами: с помощью сил и с помощью потенциальной энергии. Первый способ применим и к таким силам, для которых нельзя ввести потенциальную энергию, например для сил трения. Второй способ применим только в случае консервативных сил.

Рассмотрим перемещение частицы из одной точки потенциального стационарного поля в другую. Связь между потенциальной энергией и силой поля выражается в соответствии с уравнением (4.17) как

где потенциальная энергия Е_р <г)— функция положения частицы в поле. Следовательно, проекция F_s силы поля — вектора Е — в данной точке поля на направление перемещения dr равна с обратным знаком производной потенциальной энергии Е_р по данному направлению.

Перемещение dr можно взять в любом направлении, в частности вдоль координатных осей X, Y, Z. Связь между силой поля и потенциальной энергией как функцией координат можно представить в следующем виде:

Источник