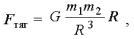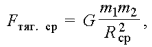потенциальная энергия тела в однородном поле тяготения

Потенциальная энергия тела в однородном поле тяготения

В чём выражается гравитационное взаимодействие тел?
Как доказать наличие взаимодействия Земли и, например, учебника физики?

Как известно, сила тяжести — консервативная сила. Теперь найдём выражение для работы силы тяготения и докажем, что работа этой силы не зависит от формы траектории, т. е. что сила тяготения также консервативная сила.

Напомним, что работа консервативной силы по замкнутому контуру равна нулю.

Пусть тело массой m находится в поле тяготения Земли. Очевидно, что размеры этого тела малы по сравнению с размерами Земли, поэтому его можно считать материальной точкой. На тело действует сила тяготения

где G — гравитационная постоянная,
М — масса Земли,
r — расстояние, на котором находится тело от центра Земли.

Пусть тело перемещается из положения А в положение В по разным траекториям: 1) по прямой АВ; 2) по кривой АА’В’В; 3) по кривой АСВ (рис. 5.15)

1. Рассмотрим первый случай. Сила тяготения, действующая на тело, непрерывно уменьшается, поэтому рассмотрим работу этой силы на малом перемещении Δr_i = r_{i + 1} — r_i. Среднее значение силы тяготения равно:

Чем меньше Δri, тем более справедливо написанное выражение r 2 _сpi = r_ir_{i + 1}.

Тогда работу силы F_сpi, на малом перемещении Δr_i, можно записать в виде

Суммарная работа силы тяготения при перемещении тела из точки А в точку В равна:

2. При движении тела по траектории АА’В’В (см. рис. 5.15) очевидно, что работа силы тяготения на участках АА’ и В’В равна нулю, так как сила тяготения направлена к точке О и перпендикулярна любому малому перемещению по дуге окружности. Следовательно, работа будет также определяться выражением (5.31).

3. Определим работу силы тяготения при движении тела от точки А к точке В по траектории АСВ (см. рис. 5.15). Работа силы тяготения на малом перемещении Δs_i равна ΔА_i = F_срiΔs_icosα_i.

Итак, можно сделать вывод, что А₁ = А₂ = А₃, т. е. что работа силы тяготения не зависит от формы траектории. Очевидно, что работа силы тяготения при перемещении тела по замкнутой траектории АА’В’ВА равна нулю.

Сила тяготения — консервативная сила.

Изменение потенциальной энергии равно работе силы тяготения, взятой с обратным знаком:

Если выбрать нулевой уровень потенциальной энергии на бесконечности, т. е. Е_пВ = 0 при r_В → ∞, то следовательно,

Потенциальная энергия тела массой m, находящегося на расстоянии r от центра Земли, равна:

Закон сохранения энергии для тела массой m, движущегося в поле тяготения, имеет вид

где υ₁ — скорость тела на расстоянии r₁ от центра Земли, υ₂ — скорость тела на расстоянии r₂ от центра Земли.

Определим, какую минимальную скорость надо сообщить телу вблизи поверхности Земли, чтобы оно в отсутствие сопротивления воздуха могло удалиться от неё за пределы сил земного притяжения.

Минимальную скорость, при которой тело в отсутствие сопротивления воздуха может удалиться за пределы сил земного притяжения, называют второй космической скоростью для Земли.

На тело со стороны Земли действует сила тяготения, которая зависит от расстояния центра масс этого тела до центра масс Земли. Поскольку неконсервативных сил нет, полная механическая энергия тела сохраняется. Внутренняя потенциальная энергия тела остаётся постоянной, так как оно не деформируется. Согласно закону сохранения механической энергии

На поверхности Земли тело обладает и кинетической, и потенциальной энергией:

где υ_II — вторая космическая скорость, М₃ и Я₃ — соответственно масса и радиус Земли.

В бесконечно удаленной точке, т. е. при r → ∞, потенциальная энергия тела равна нулю (W_п = 0), а так как нас интересует минимальная скорость, то и кинетическая энергия также должна быть равна нулю: W_к = 0.

Из закона сохранения энергии следует:

Эту скорость можно выразить через ускорение свободного падения вблизи поверхности Земли (при расчётах, как правило, этим выражением пользоваться удобнее). Поскольку то GM₃ = gR 2 ₃.

Следовательно, искомая скорость

Точно такую же скорость приобрело бы тело, упавшее на Землю с бесконечно большой высоты, если бы не было сопротивления воздуха. Заметим, что вторая космическая скорость в раза больше, чем первая.

Источник

Гравитационная потенциальная энергия

Физика > Гравитационная потенциальная энергия

Гравитационная энергия – потенциальная энергия, связанная с гравитационной силой.

Задача обучения

Основные пункты

Термины

Пример

, если добавить массу и земной радиус.

Гравитационная энергия отображает собою потенциальную, связанную с силой гравитации, потому что необходимо преодолеть земное притяжение, чтобы выполнить работу над поднятием предметов. Если объект падает от одной точки к другой внутри гравитационного поля, то сила тяжести выполнит положительную работу, а гравитационная потенциальная энергия уменьшится на ту же величину.

Допустим у нас есть книга, оставленная на столе. Когда мы переносим ее с пола на вершину стола, определенное внешнее вмешательство работает против гравитационной силы. Если же она упадет, то это работа гравитации. Поэтому процесс падения отображает потенциальную энергию, ускоряющую массу книгу и трансформирующуюся в кинетическую. Как только книга коснется пола, кинетическая энергия станет теплом и звуком.

На гравитационную потенциальную энергию влияют высота относительно конкретной точки, масса и сила гравитационного поля. Так что книга на столе уступает по гравитационной потенциальной энергии более тяжелой книга, расположенной ниже. Запомните, что высота не может применяться в вычислении гравитационной потенциальной энергии, если гравитация не выступает постоянной.

Локальное приближение

На силу гравитационного поля влияет расположение. Если изменение дистанции незначительное, то им можно пренебречь, а силу тяжести сделать постоянной (g = 9.8 м/с 2 ). Тогда для вычисления используем простую формулу: W = Fd. Восходящая сила приравнивается к весу, поэтому работа соотносится с mgh, выливающихся в формуле: U = mgh (U – потенциальная энергия, m – масса объекта, g – ускорение силы тяжести, h – высота объекта). Значение выражается в джоулях. Изменение потенциальной энергии передается как

Общая формула

Однако, если мы сталкиваемся с серьезными переменами в дистанции, то g не может оставаться постоянной и приходится применять исчисление и математическое определение работы. Чтобы рассчитать потенциальную энергию, можно интегрировать гравитационную силу относительно дистанции между телами. Тогда получим формулу гравитационной энергии:

Требушет применяет гравитационную потенциальную энергию противовеса для выброса снарядов на большие дистанции

Источник

Беседа 2. Потенциальная энергия

Коллега, о потенциальной энергии, пожалуйста, поподробнее.

Вы, мой друг, совершенно правильно интересуетесь важнейшей составляющей полной энергии.

Принято считать, что потенциальная энергия является частью общей энергии системы, зависящей от взаимного расположения материальных частиц, составляющих эту систему, и от их положений во внешнем силовом поле (гравитационное, электрическое поле).

Силовым полем мы называем ту часть пространства, в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила.

Численно потенциальная энергия системы в данном её положении равна работе, которую произведут действующие на систему силы при её перемещении из этого положения в то, где потенциальная энергия равна нулю.

Коллега, энергией обладает только пробное тело в потенциальном поле или потенциальное поле тоже?

Для ответа на Ваш вопрос открываем БСЭ (Большая Советская Энциклопедия) и в разделе «Поля физические» читаем (дословно):
«Поля физические, особая форма материи; физическая система, обладающая бесконечно большим числом степеней свободы. Примерами полей физических могут служить электромагнитное и гравитационное поля. ».

Отсюда следует, что потенциальное поле является материальной средой. Значит, как и любая материальная среда, это поле обладает энергией (соответственно, и массой). Кстати, это подтверждается, к примеру, наличием в поле электромагнитных волн, которые являются колебаниями этой материальной среды.

Конкретные границы поля определить сложно, поэтому физики давно привыкли оперировать энергией, содержащейся в единице объёма, то есть – объёмной плотностью энергии потенциального поля (измеряется в Дж/м 3 ). Возьмём, к примеру, книгу Зильбермана «Электричество и магнетизм» (Наука, М., 1970) и на стр. 136 читаем (дословно):
«В плоском конденсаторе и вообще в однородном поле плотность энергии, т. е. энергия, содержащаяся в единице объёма, постоянна и равна полной энергии, делённой на объём».

Коллега, раз уж потенциальное поле является материальной средой, то оно должно характеризоваться конкретными параметрами, которые можно вычислить и измерить.

Вы совершенно правы. Мы уже выяснили, что электрическое (потенциальное) поле характеризуется таким параметром, как объёмная плотность энергии (далее – давление, Дж/м 3 или Н/м 2 ). Кроме этого, потенциальное поле характеризуется потенциалом и его градиентом – напряженностью поля. Причем, давление, потенциал и напряженность характеризуют потенциальное поле в данной его точке, независимо от наличия в этой точке пробного тела, ибо поле, как мы уже знаем, само обладает энергией и массой.

Если потенциальную энергию (W_П, Дж) отнести к единичной массе (m, кг) или к единичному электрическому заряду (q, Кл), то получим гравитационный (v 2 = W_П/m, Дж/кг) или электрический (U = W_П/q, Дж/Кл) потенциалы.

Градиентом потенциала в данной его точке является напряженность поля:
— для гравитационного поля: g = – grad v 2 ;
— для электрического: E = – grad U (о знаке речь пойдет ниже).

Градиент (от лат. gradiens, род. падеж gradientis – шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины от одной точки пространства к другой.

С удалением от центра поля изменяется не только потенциал, но и потенциальная энергия. И её градиентом является сила, которую мы называем силой тяготения.

Уравнение F = – grad W_П показывает, что работа сил вдоль замкнутой траектории в потенциальном поле всегда равна нулю.

Коллега, какие единицы измерения наиболее приемлемы для вышеназванных параметров?

Очень хороший вопрос. СИЛА измеряется в ньютонах (Н = кг*м/с 2 ) или в Дж/м. Второй вариант записи более приемлемый, ибо сразу даёт нам указание на то, что сила является всего лишь ГРАДИЕНТОМ ЭНЕРГИИ (Дж/м). Это важно, ибо упрощает дальнейшее понимание физических процессов. Кстати, это касается не только силы, но и таких параметров, как давление и потенциал.

ПОТЕНЦИАЛ измеряется в м 2 /с 2 или в Дж/кг (для гравитационного поля) и в (кг/Кл)*( м 2 /с 2 ) или Дж/Кл (для электрического поля). И здесь более приемлемым является второй вариант записи, ибо сразу указывает на значение потенциальной энергии, отнесенной к единице массы (Дж/кг) для гравитационного поля или отнесенной к единице электрического заряда (Дж/Кл) для электрического поля.

И наконец, коллега, давайте рассмотрим, как определяется значение потенциальной энергии.

Пожалуй, теперь мы готовы решать и эту проблему. Значение потенциальной энергии определяется двумя способами:
— упрощенный (приближенный) – для однородного поля;
— общий (истинный) – для неоднородного поля, которое нас реально и окружает.

Потенциальное поле можно условно считать однородным, если вектор напряженности во всех его точках имеет одно и то же значение и направление. К примеру, для гравитационного поля это правило можно применить только у поверхности Земли на небольшом её участке (скажем, в лабораторном опыте). В этом случае для упрощения расчетов значение потенциальной энергии пробного тела на поверхности Земли условно принимается равной нулю, а её значение в любой другой точке определяется из уравнения:

W_П = mgh, Дж,
где g – напряженность гравитационного поля (Н/кг), а h – вертикальное расстояние (м) от поверхности Земли до пробного тела массой m (кг).

Здесь знак перед значением потенциальной энергии принципиального значения не имеет.

Коллега, но ведь это и есть наиболее распространенный способ определения потенциальной энергии.

К сожалению, многие учебники физики на этом и завершают определение потенциальной энергии. Но не все. Взять, к примеру, Общий курс физики Сивухина (Москва, МФТИ, 2005) или американский курс Физики в переводе под редакцией Ахматова (Москва, Наука, 1974).

Здесь рассматривается:
— уже известный нам способ определения потенциальной энергии пробного тела в однородном поле тяжести у поверхности Земли (том 1, стр. 144-145 первого источника и часть III, стр.152-157 второго источника);
— и общий способ определения потенциальной энергии для неоднородного поля (том 1, стр. 145-146 первого источника и часть III, стр.157-159 второго источника).

Общий способ расчета дает уже отрицательное значение потенциальной энергии:
— уравнение (25.6) W(U) = – GMm/r в первом источнике и
— уравнение W(Ur) = – GMm/r – во втором.

Отрицательное значение потенциальной энергии здесь объясняется следующим образом:
— в первом источнике (цитата): «Максимальной энергией притягивающиеся массы обладают при бесконечном расстоянии между ними. В этом положении потенциальная энергия считается равной нулю. Во всяком другом положении она меньше, т. е. отрицательна»;
— во втором источнике дано доказательство правильности уравнения W(Ur) = – GMm/r.

И действительно, свободно падающее к центру поля тело теряет свою потенциальную энергию, которая переходит в кинетическую. Значит, потенциальная энергия с уменьшением расстояния между центрами масс (M и m) уменьшается и, наоборот, с увеличением расстояния – увеличивается.

Учитывая, что в уже известном нам уравнении W_П = – GMm/r символ радиуса находится в знаменателе, то предельно ясно, что с увеличением расстояния (значение радиуса стремится к бесконечности) потенциальная энергия увеличивается до… нуля. Такое возможно только в том случае, если потенциальная энергия во всяком другом положении отрицательна.

Вывод: потенциальная энергия для всех материальных частиц отрицательна.

Отсюда следует, что значение гравитационного потенциала v 2 = W_П/m = – GM/r тоже отрицательно. И подтверждением этому является уравнение (3) в разделе «Тяготение» (стр. 772) Физического Энциклопедического Словаря или аналогичного раздела Большой Советской Энциклопедии.

Аналогично определяется значение потенциальной энергии и электрического потенциала в электрическом поле. Причем далее мы убедимся в том, что потенциальная энергия и её объёмная плотность (давление) ОДИНАКОВЫ и для гравитационного, и для электрического полей.

Коллега, теперь попробуйте записать Ваше высказывание в виде формулы.

Формулы пишут математики, а физики пользуются уравнениями. Необходимые уравнения здесь уже приводились. Однако попробуем, все же, обойтись пока без них, тем более – без «формул».

Для этого используем бытовые наблюдения, которые подсказывают: чтобы испарить воду, кипящую в чайнике, нужно сжечь некоторое количество дров или газа. Другими словами, нужно совершить работу. С помощью термометра можно убедиться, что температура кипящей воды и температура пара над ней одинаковы. Следовательно, одинакова и средняя энергия движения частиц в кипящей воде и в паре.

Вывод: тепловая энергия, передаваемая кипящей воде от топлива, преобразуется в энергию взаимодействия частиц испаряющейся воды. Значит, энергия связи частиц в кипящей воде меньше, чем в водяном паре. Но в паре эта энергия практически равна нулю, следовательно, энергия взаимодействия частиц в жидкости меньше нуля, т.е. отрицательна.

Коллега, Ваши доводы убедительны и примеры Вы приводите неопровержимые. Однако не все думают так же.

Однако математики так не думают. Для них гравитационное поле является ОДНОРОДНЫМ с неизменной напряженностью гравитационного поля (вроде этот параметр и не зависит от радиуса). Значение потенциальной энергии они определяют по упрощенной формуле W = mgh. Они не связывают h с радиусом поля, а считают его простым отрезком между двумя произвольными точками этого поля. Поэтому для них потенциальная энергия может принимать нулевое значение в любой понравившейся им точке. Нонсенс, но бывает и такое.

Но есть ещё и «физико-математики». Их мнение зависит от того, насколько они физики или математики.

Коллега, почему Вы считаете, что математики «тяготеют» к однородному полю?

В подтверждение этому открываем Краткий курс математического анализа (Бермант, Араманович, 2005) и на стр. 520 в разделе «Теория поля» читаем:
«Векторное поле называется однородным, если А(Р) — постоянный вектор, т.е. Ах, Аy и Az — постоянные величины.
Примером однородного поля может служить, например, поле тяжести».

Теперь Вы и сами видите, что математики гравитационное поле называют «полем тяжести» и «всерьёз» считают его однородным. И это не просто безобидное заблуждение, ибо оно мешает нам осознать Природу гравитации. Однако, об этом мы поговорим немного позже.

Источник

Потенциальная энергия тела в гравитационном поле

Следующий шаг предполагает знакомство учеников с потенциальной энергией тела в поле тяготения. Энергия взаимодействия тела с гравитационным полем Земли описывается формулой Еп = mgh только в том случае, если гравитационное поле Земли можно считать однородным, не зависящим от координат. Гравитационное поле определяется законом всемирного тяготения:

где R – радиус-вектор, проведенный от центра масс Земли (принятого за начало отсчета) до данной точки (напомним, что в законе тяготения тела считаются точечными и неподвижными). По аналогии с электростатикой можно записать эту формулу в виде:

и назвать вектором напряженности гравитационного поля в данной точке. Ясно, что это поле изменяется с расстоянием от создающего поле тела. Когда же можно считать гравитационное поле с достаточной точностью однородным? Очевидно, это возможно в области пространства, размеры которой h много меньше расстояния до центра поля R. Иными словами, если вы рассматриваете падение камня с верхнего этажа дома, можно спокойно пренебречь разницей в значении гравитационного поля на верхнем и нижнем этажах. Однако, изучая движение планет вокруг Солнца, нельзя считать, что планета движется в однородном поле, и следует пользоваться общим законом тяготения.

Еп = Еп1 – Еп = Fтяг. ср s,

где Fтяг. cр – величина средней силы тяготения на участке s = R1 – R0 перемещения тела в направлении силы. По закону всемирного тяготения величина силы есть:

Если расстояния R1 и R0 мало отличаются друг от друга, то можно заменить расстояние Rср2 произведением R1R0. Тогда:

Мы получили формулу, которая указывает на две особенности потенциальной энергии гравитационного взаимодействия (ее еще называют энергией тяготения):

1. В самой формуле уже заложен выбор нулевого уровня потенциальной энергии тяготения, а именно: энергия гравитационного взаимодействия тел обращается в нуль, когда расстояние между рассматриваемыми телами бесконечно велико. Обратите внимание, что такой выбор нулевого значения энергии гравитационного взаимодействия тел имеет наглядную физическую интерпретацию: при бесконечно большом удалении тел друг от друга они практически перестают гравитационно взаимодействовать.

2. Поскольку любое реальное расстояние, например между Землей и ракетой, конечно, энергия гравитационного взаимодействия при таком выборе начала отсчета всегда отрицательна.

На рис. 5 приведен график зависимости энергии гравитационного взаимодействия ракеты с Землей от расстояния между центром Земли и ракетой. Он отражает обе особенности энергии тяготения, о которых мы говорили: показывает, что эта энергия отрицательна и возрастает к нулю при увеличении расстояния между Землей и ракетой.

Энергия связи

Полученные учениками знания о том, что энергия может быть как положительной, так и отрицательной величиной, должны найти свое применение при изучении энергии связи частиц вещества в разных его агрегатных состояниях. Например, школьникам можно предложить следующие качественные рассуждения.

Мы уже убедились, что частицы вещества всегда хаотично движутся. Именно наделив частицы способностью к такому движению, мы смогли объяснить целый ряд явлений природы. Но тогда почему не разлетаются на отдельные частицы столы и карандаши, стены домов и мы сами?

Приходится предположить, что частицы вещества взаимодействуют, притягиваются друг к другу. Только достаточно сильное взаимное притяжение частиц способно удерживать их друг около друга в жидкостях и твердых телах, не давать им быстро разлетаться в разные стороны. Но почему тогда не удерживаются друг около друга частицы в газах, почему они разлетаются? По-видимому, в газах взаимосвязь частиц недостаточна для их удержания.

В механике для оценки взаимодействия (связи) тел мы использовали такую физическую величину, как потенциальная энергия взаимодействия. В кинетической теории вещества связь частиц вещества характеризуется энергией их взаимодействия Есв (эта энергия не всегда потенциальная). Тот факт, что частицы в жидкости и в твердом теле удерживают друг друга, а в газах нет, подсказывает, что энергия связи частиц друг с другом в этих средах разная.

Газ. В газе расстояние между частицами велико и их связь слаба. Частицы изредка сталкиваются друг с другом и со стенками сосуда. Соударения носят упругий характер, т.е. полная энергия и полный импульс сохраняются. В промежутках между соударениями частицы движутся свободно, т.е. не взаимодействуют. Разумно считать, что энергия взаимодействия (связи) частиц в газе приближенно равна нулю.

Жидкость. В жидкости частицы сближены, они частично соприкасаются. Их взаимное притяжение велико и характеризуется энергией связи Есв(вода). Чтобы оторвать одну молекулу от основной массы жидкости, необходимо совершить работу A > 0. В результате молекула станет свободной, как в газе, т.е. ее энергию связи можно будет считать равной нулю. По закону сохранения энергии Есв(вода)+ А = 0, откуда Есв(вода) = –А

Источник