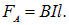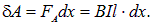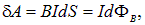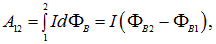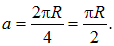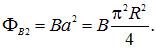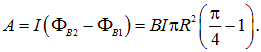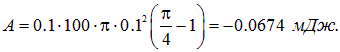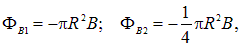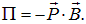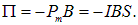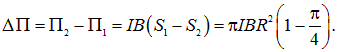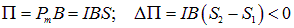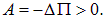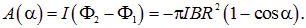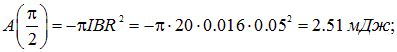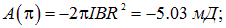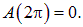работа при перемещении проводника в магнитном поле

Работа, совершаемая при перемещении проводника с током в магнитном поле

На проводник с током в магнитном поле действуют силы, подчиняющиеся закону Ампера (3.1.4) и часто называемые поэтому силами Ампера.

Вычислим работу, совершаемую этими силами при перемещении проводника с током в магнитном поле. При малом перемещении dr элемента d/ проводника с током I работа силы Ампера ДР равна:

Подставив (3.1.4) в (3.5.6), получим:

Из векторной алгебры известно, что смешанное произведение 3-х векторов не изменится, если в нем произвести циклическую перестановку сомножителей:

Элементарная работа ЪА амперовых сил при малом перемещении проводника конечной длины равна сумме элементарных работ 8А* амперовых сил для всех малых участков этого проводника:

Интегрирование проводится по всей длине проводника, сила тока по длине не изменится. Используя (3.5.7) и (3.5.8), запишем выражение для магнитного потока dO сквозь поверхность, прочерчиваемую всем проводником при малом перемещении dr этого проводника:

Если проводник, ток в котором I = const, совершает конечное перемещение, то работа амперовых сил на этом перемещении:

Работа, совершаемая силами Ампера при перемещении в магнитном поле проводника, ток в котором постоянен, равна произведению силы тока на магнитный поток сквозь поверхность, которую прочерчивает проводник при своем движении.

Если в процессе перемещения контура сила тока остается постоянной, для определения работы силы Ампера используется выражение:

Итак, работа, совершаемая силами Ампера при перемещении в магнитном поле замкнутого контура, по которому проходит постоянный ток, равна произведению силы тока на изменение магнитного потока сквозь поверхность, ограниченную контуром.

При выводе формул мы рассматривали простейший замкнутый контур, состоящий из одного плоского витка провода. Однако полученные выражения в равной степени справедливы и для контуров любой формы.

Полученному выражению (3.5.12) для работы по перемещению контура с током в магнитном поле можно придать другой вид.

На контур с током в магнитном поле действует вращательный момент, определяемый выражением (3.5.3), и энергия контура с током в магнитном поле зависит от ориентации контура.

Элементарная работа, совершаемая против сил поля при (медленном) повороте плоскости контура с током на угол da (рис. 3.5.2), определяется выражением

Работа A = jSA идет на увеличение потенциальной энергии Wn контура с током в магнитном поле.

Эта энергия соответствует работе, совершаемой при внесении небольшого контура с током / в данную точку поля из бесконечности. Полагаем, что 5(х = оо) = 0 и значения индукции магнитного поля В(х) различаются незначительно для сторон а контура (рис. 3.5.2)

Источник

8.1. Опыты Фарадея. Работа по перемещению проводника с током в магнитном поле

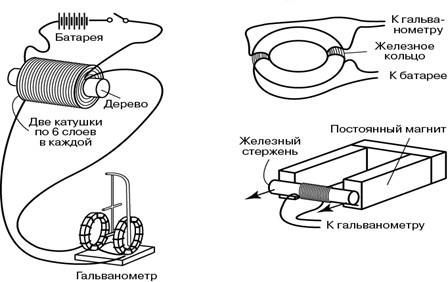
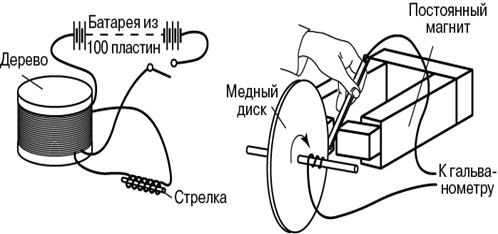
Познакомимся с опытами, которые проводил Фарадей (рис. 8.3, 8.4).

Рис. 8.3. Опыты Фарадея

Рис. 8.4. Опыты Фарадея

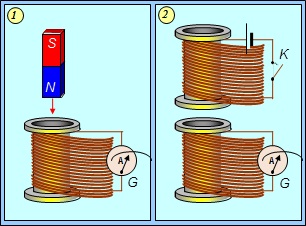
Для более близкого знакомства с явлением электромагнитной индукции, подробно рассмотрим два опыта (рис. 8.5).

Рис. 8.5. ЭДС индукции возникает в катушке, когда:
1 — к нейприближается постоянный магнит; 2 — когда меняется ток в соседней катушке

На левом рисунке изображена катушка, подсоединенная к гальванометру G. Если приближать к витку постоянный магнит, стрелка гальванометра отклонится: по катушке пройдет ток. При неподвижном же магните ничего не происходит. На правом рисунке вблизи такой же катушки с гальванометром помещена другая катушка. Если замкнуть ключ К, то по верхней катушке пойдет электрический ток. В этот момент стрелка гальванометра отклонится, зарегистрировав импульс тока в нижней катушке. То же самое произойдет при размыкании ключа К.

В обоих случаях виток с гальванометром не был подсоединен к источнику тока. Тем не менее, ток в нем появился, что свидетельствует о возникновении какой-то электродвижущей силы. Ее называют ЭДС электромагнитной индукции. Рассмотренные опыты приводят к выводу, что ЭДС индукции возникает, когда что-то меняетсяв системе проводников.

Обратимся к одному из возможных вариантов изменений в системе — перемещению одного из ее проводников. Поскольку на проводник с током действует сила, то при перемещении этого проводника будет совершаться работа. Рассмотрим устройство на рис. 8.6.

Рис. 8.6. Работа по перемещению проводника с током в магнитном поле

Видео 8.3. К рисунку 8.6: возникновение индукционного тока при движении небольшого участка замкнутого проводящего контура в магнитном поле.

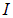
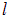
Пусть отрезок проводника с током длиной перемещается из положения 1 в положение 2 под действием силы Ампера в магнитном поле

Работа, совершаемая полем по перемещению проводника на расстояние 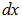, равна

Произведение 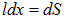есть элемент площади, которую пересек отрезок проводника при своем движении из положения 1 в положение 2. Таким образом,

где 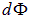— изменение потока вектора магнитной индукции через площадь, охватываемую током.

Согласно (8.3) работа, совершаемая магнитным полем при перемещении в нем подвижного проводника с током, равна произведению силы тока I в проводнике и потока 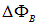сквозь поверхность, заметаемую проводником при его движении.

Полученному результату можно дать несколько иную интерпретацию. Токи, текущие в проводнике, так или иначе замкнуты, образуют контур. Если перемещать или деформировать контур с током во внешнем магнитном поле, то полная работа определится суммированием (интегрированием) элементарных работ

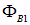
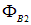
где и — значения потока магнитной индукции в начальном и конечном состоянии контура с током (мы предполагали, что ток в контуре при этом не меняется).

Пример 1. По кольцу радиусом 10 см, сделанному из тонкого гибкого провода, течет ток 100 А. Перпендикулярно плоскости кольца создано внешнее однородное магнитное поле 0,1 Тл. Направление этого поля совпадает с направлением собственного магнитного поля кругового тока на его оси. Определить работу А внешних сил, которую надо затратить, чтобы превратить кольцо в квадрат, не меняя его ориентации относительно внешнего поля. Работой против упругих сил пренебречь. Ток в кольце поддерживается постоянным. Как изменится результат, если внешнее поле будет иметь противоположное направление?

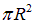
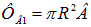
Решение. 1-й способ. Площадь кольца равна , так что поток магнитной индукции через кольцо равен . При деформации кольца в квадрат его периметр не изменится, так что сторона квадрата в четыре раза меньше длины окружности кольца

Поэтому величина работыбудет равна

Подставляем численные значения и получаем

Работа получилась отрицательной, то есть ее надо совершить против сил поля. Действительно, при правовинтовом (по условию) расположении тока и внешнего поля сила Ампера стремится растянуть кольцо- увеличить его площадь. Превращая кольцо в квадрат, мы уменьшаем площадь, тем самым совершаем работу против сил поля.

Если поле имеет обратный знак, то эту работу совершит сила Ампера, и она будет положительной. При решении задачи в этом случаепотоквнешнего поля отрицателен (внешнее поле изменило своё направление на противоположное, а нормаль к поверхности, ограниченной контуром, осталась прежней, связанной правилом правого винта с направлением тока в контуре). Поэтому

и для работы 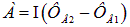получится то же выражение, но с обратным знаком.

Решение. 2-й способ. Как известно, магнитный момент витка с током равен 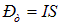, а его потенциальная энергия в магнитном поле определяется выражением

При правовинтовом расположении тока и магнитного поля угол между векторами Р_m и В равен нулю, так что

Разность потенциальных энергий при деформации витка равна

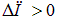
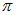
Поскольку , потенциальная энергия при деформации увеличилась, на что надо затратить работу против сил поля. При изменении направления поля угол между ним и магнитным моментом равен , так что

Естественно, мы получили те же результаты, что и при первом способе решения.

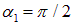
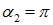
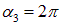
Пример 2. Круглый виток с током 20 А свободно установился в однородном магнитном поле с магнитной индукцией 0,016 Тл. Радиус витка равен 5 см. Определить работу, которую надо совершить, чтобы повернуть виток на углы , , относительно оси, совпадающей с диаметром витка.

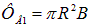
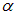
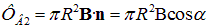
Решение. Раз в начальном положении виток установился свободно, значит его магнитный момент параллелен вектору В. Поток через плоскость витка положителен и равен . При повороте витка на угол поток станет равным . Совершаемая при этом работабудет равна

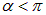
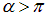
При углах поворота работа отрицательна: контур находится в состоянии устойчивого равновесия, и надо затратить усилия против сил поля, чтобы вывести его из равновесного состояния. Но при контур уже сам стремится к положению равновесия, так что работа будет совершаться силами поля, и это частично компенсирует затраченную прежде работу. При полном обороте работа сил поля в точности равна работе внешних сил, так что полная работа оказывается равной нулю.

Этот пример также можно решить другим способом — в терминах потенциальной энергии взаимодействия магнитного момента с полем.

Отметим, что использовать для вычисления работы магнитный момент контура с током можно лишь в том случае, если внешнее поле однородно или слабо неоднородно. Последнее означает, что внешнее поле в пределах контура меняется настолько мало, что этим можно пренебречь. Если внешнее поле в пределах контура меняется существенно, то точный результат для работы может быть получен только путем интегрирования работы сила Ампера с учетом величины и направления внешнего поля в точке её приложения. Такой подход и приводит к точной формуле (8.4), полученной выше на примере системы простейшей геометрии, изображенной нa рис. 8.2. Таким образом, формула (8.4) точная и общая — для задачи любой геометрии.

Источник

Курс лекций по физике Трофимова Для студентов инженерно-технических специальностей

Работа по перемещению проводника и контура с током в магнитном поле

На проводник с током в магнитном поле действуют силы, определяемые законом Ампера (см. § 111). Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки, рис. 177), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током.

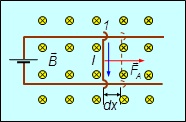
Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемещаться), помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна

Под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

так как ldx=dS — площадь, пересекаемая проводником при его перемещении в магнитном поле, BdS=dФ — поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,

(121.1) Динамика Физика решение задач

т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива и для произвольного направления вектора В.

Вычислим работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение М’, изображенное на рис. 178 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно разобьем на два соединенных своими концами проводника: AВС и CDА.

Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA1) и CDA (dA2), т. е.

Силы, действующие на участок AВС контура, образуют с направлением перемещения тупые углы, поэтому совершаемая ими работа dA1 (121.4)

Подставляя (121.3) и (121.4) в (121.2), получим выражение для элементарной работы:

где dФ2—dФ1=dФ’ — изменение магнитного потока сквозь площадь, ограниченную контуром с током. Таким образом,

т. е. работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Формула (121.6) остается справедливой для контура любой формы в произвольном магнитном поле.

14.1. Тонкое кольцо массой 15 г и радиусом 12 см несет заряд, равномерно распределенный с линейной плотностью 10 нКл/м. Кольцо равномерно вращается с частотой 8 с–1 относительно оси, перпендикулярной плоскости кольца и проходящей через ее центр. Определить отношение магнитного момента кругового тока, создаваемого кольцом, к его моменту импульса. [251 нКл/кг]

14.2. По проводу, согнутому в виде квадрата со стороной, равной 60 см, течет постоянный ток 3 А. Определить индукцию магнитного поля в Центре квадрата. [5,66 мкТл]

14.3. По двум бесконечно длинным прямым параллельным проводникам, расстояние между которыми равно 25 см, текут токи 20 и 30 А в противоположных направлениях. Определить магнитную индукцию В в точке, удаленной на r1=30 см от первого и r2=40 см от второго проводника. [9,5 мкТл]

14.4. Определить магнитную индукцию на оси тонкого проволочного кольца радиусом 10 см, по которому течет ток 10 А, в точке, расположенной на расстоянии 15 см от центра кольца. [10,7 мкТл]

14.5. Два бесконечных прямолинейных параллельных проводника с одинаковыми токами, текущими в одном направлении, находятся друг от друга на расстоянии R. Чтобы их раздвинуть до расстояния 3R, на каждый сантиметр длины проводника затрачивается работа A=220 нДж. Определить силу тока в проводниках. [10 А]

14.6. Определить напряженность поля, создаваемого прямолинейно равномерно движущимся со скоростью 500 км/с электроном в точке, находящейся от него на расстоянии 20 нм и лежащей на перпендикуляре к скорости, проходящем через мгновенное положение электрона. [15,9 А/м]

14.7. Протон, ускоренный разностью потенциалов 0,5 кВ, влетая в однородное магнитное поле с индукцией 0,1 Тл, движется по окружности. Определить радиус этой окружности. [3,23 см]

14.8. Определить, при какой скорости лучок заряженных частиц, проходя перпендикулярно область, в которой созданы однородные поперечные электрическое и магнитное поля с E=10 кВ/м и В= 0,2 Тл, не отклонятся. [50 км/с]

14.9. Циклотрон ускоряет протоны до энергии 10 МэВ. Определить радиус дуантов циклотрона при индукции магнитного поля 1 Тл. [>47 см]

14.10. Через сечение медной пластинки толщиной 0,1 мм пропускается ток 5 А. Пластинка помещается в однородное магнитное поле с индукцией 0,5 Тл, перпендикулярное ребру пластинки и направлению тока. Считая концентрацию электронов проводимости равной концентрации атомов, определить возникающую в пластине поперечную (холловскую) разность потенциалов. Плотность меди 8,93 г/см3. [1,85 мкВ]

14.11. По прямому бесконечно длинному проводнику течет ток 15 А. Определить, пользуясь теоремой о циркуляции вектора В, магнитную индукцию В в точке, расположенной на расстоянии 15 см от проводника. [20 мкТл]

14.12. Определить, пользуясь теоремой о циркуляции вектора В, индукцию и напряженность магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей 300 витков, протекает ток 1 А. Внешний диаметр тороида равен 60 см, внутренний — 40 см. [0,24 мТл; 191 А/м]

14.13. Поток магнитной индукции сквозь площадь поперечного сечения соленоида (без сердечника) Ф=5 мкВб. Длина соленоида l=25 см. Определить магнитный момент pm этого соленоида. [1 А × м2]

14.14. Круглая рамка с током площадью 20 см2 закреплена параллельно магнитному полю (В=0,2 Тл), и на нее действует вращающий момент 0,6 мН×м. Рамку освободили, после поворота на 90° ее угловая скорость стала 20 с–1. Определить: 1) силу тока, текущего в рамке; 2) момент инерции рамки относительно ее диаметра. [1) 1,5 А; 2) 3 × 10–6 кг×м2]

Источник

Работа по перемещению проводника с током в магнитном поле

На проводник с током в магнитном поле и действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемычки, рис. 15), то под действием силы Ампера он будет в магнитном поле перемещаться. Следовательно, магнитное поле совершает работу по перемещению проводника с током.

Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемешаться), помещенный в однородное внешнее магнитное поле перпендикулярное плоскости контура. При указанных на рис.15 направлениях тока и поля сила, направление которой определяется по правилу левой руки, а модуль – по закону Ампера (2.2), равна

Под действием этой силы проводник переменится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

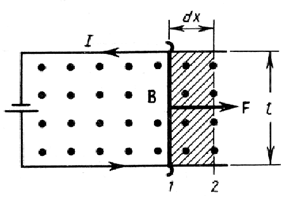
так как l dx = dS – площадь, пересекаемая проводником при его перемещении в магнитном поле, В dS = dФ – поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,

т.е. работа по перемещению проводника с током

в магнитном поле равна произведению силы тока

Рис.15. на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива для произвольного направления вектора В.

РЕЗЮМЕ:

Знать значения терминов: правило правой руки, правило левой руки

Пример решения задач по изучаемой теме

Источник