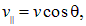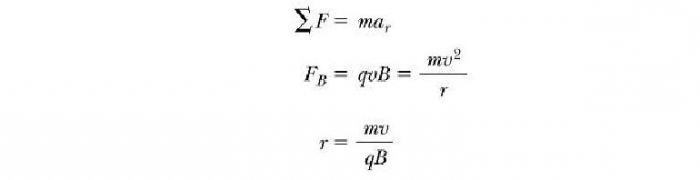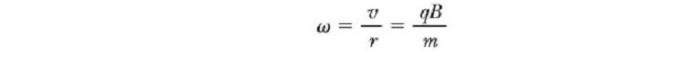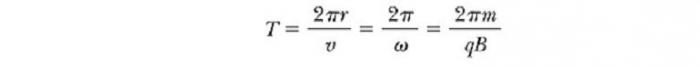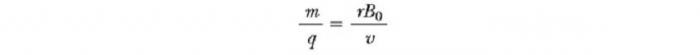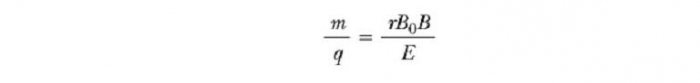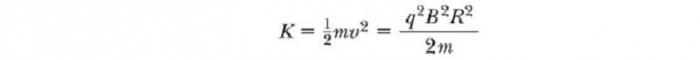радиус траектории частицы в магнитном поле

5.3. Движение заряда в однородном магнитном поле

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

из которого легко получить выражение для угловой скорости частицы

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

Кинетическая энергия протона будет

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).

Источник

Учебники

Журнал «Квант»

Общие

§14. Движение заряженных частиц в электрическом и магнитном полях

14.2 Плоское движение заряженной частицы в однородном магнитном поле.

При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы.

Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля (Рис. 89). Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля \(

\vec B\), то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным F_л = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона

из которого находим

Найдем период обращения частицы в магнитном поле

Из этой формулы следует интересный и неожиданный вывод [1] – период вращения частицы в магнитном поле не зависит от ее скорости. Частота вращения выражается формулой

и называется циклотронной частотой.

14.2.1 Циклотрон.

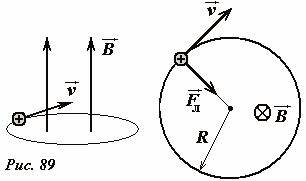
Постоянство частоты вращения частиц в магнитном поле используется в циклотроне одном из типов ускорителей заряженных частиц – ионов.

Ускорители подобного типа были разработаны и построены в 30-х годах ХХ века и сыграли (и продолжают играть) большую роль в развитии ядерной физики. Не смотря на простоту основных принципов работы ускорителя, циклотрон является очень сложным инженерным сооружением, включающим (помимо описанных элементов) источники питания (электромагнитов, источников частиц, ускоряющей системы, системы регистрации и д.р.), вакуумную систему, блоки управления и регистрации и т.д.

14.2.2 Масс-спектроскопия.

Характеристики движения частиц в магнитном поле (радиус траектории, время движения) зависят от их масс и зарядов. Изучение движения частиц в магнитных полях является основой масс-спектроскопии – метода исследования вещества по спектру [3] масс атомов и молекул, входящих в его состав. Сущность метода состоит в том, что ионизованные атомы и молекулы, проходя через магнитное поле, пространственно разделяются и регистрируются в различных точках. Первоначальными задачами масс-спектроскопии были исследование изотопного состава элементов и прецизионное (точное) измерение масс атомов. В дальнейшем масс-спектроскопия выросла в универсальный аналитический метод, применяющийся в экспериментальной физике, химии, биологии, геологии, технике. Приборы, позволяющие разделять и регистрировать частицы, называются масс-спектрометрами.

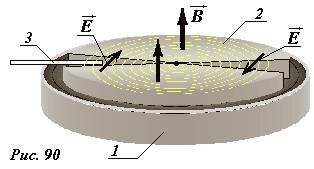
Принцип действия масс-спектрометра показан на рис. 91. Исследуемый образец специальными методами (испарением, электронным ударом) переводится в газообразное состояние, затем образовавшийся газ ионизируется в источнике 1. Затем ионы ускоряются электрическим полем и формируются в узкий пучок в ускоряющем устройстве 2 и через узкую входную щель 3 попадают в камеру 4, в которой создано однородное поперечное магнитное поле. В камере ионы движутся по дуге окружности и попадают на экран 5, где регистрируется место их попадания. Методы регистрации могут быть различными – фотографические, электронные и т.д. Радиус траектории зависит от массы и заряда иона, поэтому разные ионы попадают на экран на различном расстоянии от источника, что и позволяет их разделять и анализировать состав образца.

Найдем координату точки попадания иона на экран в зависимости от его массы, заряда и параметров прибора. В ускоряющем устройстве, пройдя разность потенциалов Δϕ, приобретают скорость υ₀, которая может быть найдена из уравнения закона сохранения энергии

из которого следует

Начальной скоростью ионов можно пренебречь, так как обычно она значительно меньше скорости после ускорения. Кроме того, в некоторых приборах применяют дополнительные устройства для выделения частиц имеющих близкие значения скоростей. В магнитном поле ионы движутся по окружности радиуса

которая зависит от отношения массы к заряду частицы. Координата попадания иона на экран равна диаметру окружности

В большинстве случаев ионы являются однозарядными (т.е. атомы и молекулы в процессе ионизации теряют один электрон), поэтому фактически прибор разделяет ионы по их массе, формируя масс-спектр исследуемого образца. Если в исходном образце присутствуют различные ионы, то на экране образуется несколько полос, координаты которых позволяют определить состав исходной смеси. Одной из важнейших характеристик масс-спектрометров является их разрешающая способность – характеристика, указывающая, при какой минимальной разности масс, ионы могут различены. Разрешающая способность прибора ограничена, так как полосы на экране не являются абсолютно тонкими, они всегда несколько размыты, имеют некоторую ширину. Если разность координат полос, соответствующих ионам мало различающихся масс (например изотопам одного химического элемента), оказывается меньше ширины полос, то эти полосы сольются, что сделает невозможным разделение (разрешение) двух типов ионов. Кроме того, ширина образующейся полосы Δx определяет погрешность определения массы иона.

Из формулы (4) следует, что масса иона рассчитывается по формуле

Если считать, что основную погрешность в определение массы вносит погрешность определения координаты полосы (то есть ее ширина) Δx, то погрешность определения массы следует рассчитывать по формуле

а относительная погрешность равна

Таким образом, уменьшение ширины образующейся полосы является одной из важнейших задач разработчиков масс-спектрометров.

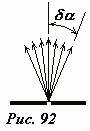
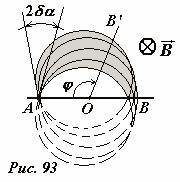
Не случайно в рассматриваемом приборе ионы пролетают половину окружности (их угол поворота равен π) – в этом случае однородное поперечное поле частично фокусирует ионы на регистрирующем экране. Рис. 93 иллюстрирует фокусировку пучка частиц в однородном поперечном магнитном поле. В идеальном случае, когда все частицы вылетают строго в одном направлении, нет необходимости заставлять ионы пролетать половину окружности. В принципе, экран OB’ можно расположить под произвольным углом ϕ. Однако, если ионы вылетают из щели A в пределах некоторого угла 2δα, то пучок ионов (на рис. 93 заштрихован) обладает некоторой шириной, причем его ширина минимальна именно при угле поворота ионов равному π. Найдем эту минимальную ширину пучка, которая равна ширине полосы на экране AB.

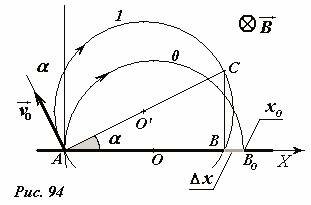
Пусть ион влетает в область магнитного поля под углом α к нормали (Рис. 94) и затем движется по дуге окружности ACB. Для сравнения на рисунке изображена «идеальная» траектория AB₀ частицы, влетевшей перпендикулярно экрану. Если вектор начальной скорости частицы \(

Эта координата максимальна для «идеальной» траектории α = 0 и уменьшается при увеличении угла отклонения вектора начальной скорости, причем не зависимо от того в какую сторону. Если максимальный угол отклонения равен δα, то ширина полосы равна

при малом δα следует воспользоваться приближенной формулой \(

а относительное уширение полосы оказывается равным

Как следует из полученного результата, уширение полосы является малой величиной более высокой степени (действительно (δα) 2 14.2.3 Магнитная отклоняющая система.

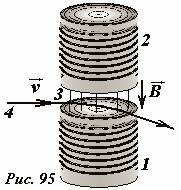
Магнитное поле также используется для отклонения пучков частиц. Причем магнитные отклоняющие системы электронных пучков в телевизионных трубках (кинескопах) и осциллографах используются гораздо чаще электростатических. Магнитная отклоняющая система проста – состоит из двух электромагнитов 1-2, в зазоре 3 которых проходит электронный пучок 4 (Рис. 95).

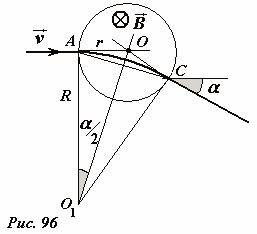
Найдем угол отклонения электронного луча в этом случае. Пусть область, занятая однородным магнитным полем индукции \(

\vec B\) (зазор между торцами магнитов, магнитным полем вне этой области можно пренебречь) имеет форму цилиндра радиуса r (Рис. 96). Для простоты будем считать, что пучок электронов движется по направлению к центру этой области и попадает в нее в точке A. Под действием магнитного поля пучок отклоняется и движется по дуге окружности AC, радиус которой равен

угол отклонения луча α легко находится из рисунка. Из прямоугольного треугольника AOO₁ следует, что

При малых углах (когда тангенс приблизительно равен самому углу) отклонение пропорционально индукции поля, которая в свою очередь пропорциональна силе тока электромагнита. Изменяя величину этого тока можно регулировать направление пучка электронов.

Источник

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?

Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).

Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:

где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.

Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.

Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.

Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.

* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑

Источник

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

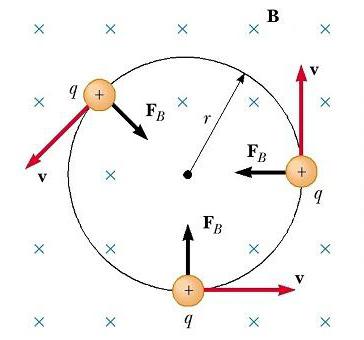
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

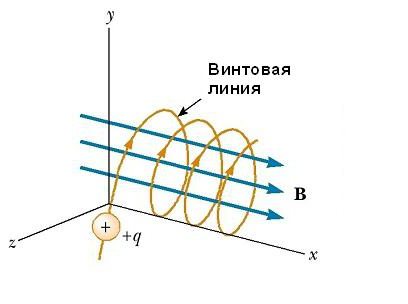
Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

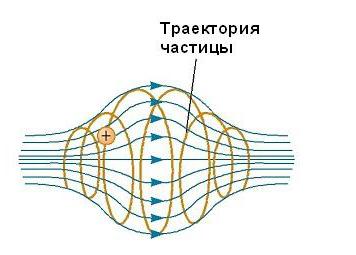
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

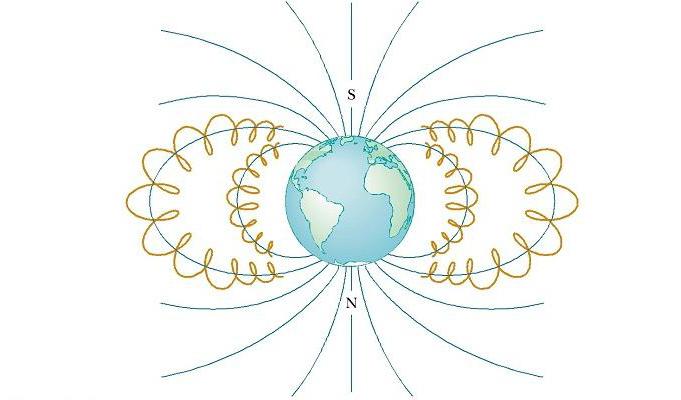
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

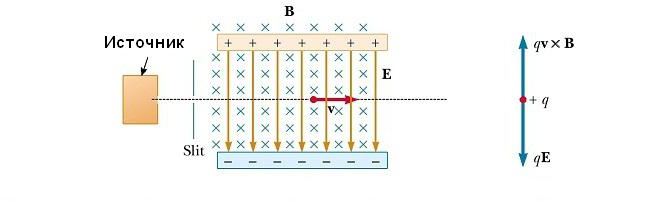
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

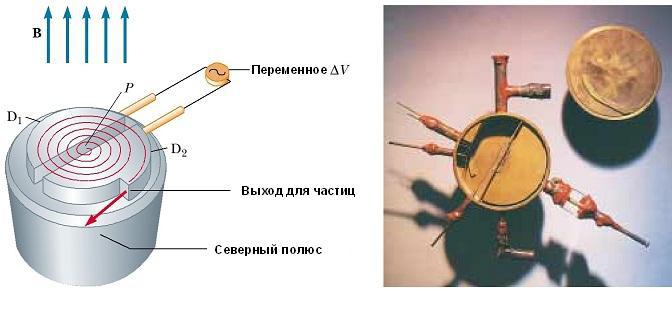
Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Источник