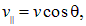радиус вращения частицы в магнитном поле

Представление о магнитном поле

Мы все знаем, что такое постоянные магниты. Магниты – это металлические тела, притягивающиеся к другим магнитам и к некоторым металлам. То, что располагается вокруг магнита и взаимодействует с окружающими предметами (притягивает или отталкивает некоторые из них), называется магнитным полем.

Источником любого магнитного поля являются движущиеся заряженные частицы. А направленное движение заряженных частиц называется электрическим током. То есть, любое магнитное поле вызывается исключительно электрическим током.

За направление электрического тока принимают направление движения положительно заряженных частиц. Если же движутся отрицательные заряды, то направление тока считается обратным движению таких зарядов. Представьте себе, что по кольцевой трубе течет вода. Но мы будем считать, что некий «ток» при этом движется в противоположном направлении. Электрический ток обозначается буквой I.

В металлах ток образуется движением электронов – отрицательно заряженных частиц. На рисунке ниже, электроны движутся по проводнику справа налево. Но считается, что электрический ток направлен слева направо.

Это произошло потому, что когда начали изучение электрические явления, не было известно, какими именно носителями чаще всего переносится ток.

Если мы посмотрим на этот проводник с левой стороны, так, чтобы ток шел «от нас», то магнитное поле этого тока будет направлено вокруг него по часовой стрелке.

Если рядом с этим проводником расположить компас, то его стрелка развернется перпендикулярно проводнику, параллельно «силовым линиям магнитного поля» — параллельно черной кольцевой стрелке на рисунке.

Если мы возьмем шарик, имеющий положительный заряд (имеющий дефицит электронов) и бросим его вперед, то вокруг этого шарика появится точно такое же кольцевое магнитное поле, закручивающееся вокруг него по часовой стрелке.

Ведь здесь тоже имеет место направленное движение заряда. А направленное движение зарядов есть электрический ток. Если есть ток, вокруг него должно быть магнитное поле.

Движущийся заряд (или множество зарядов – в случае электрического тока в проводнике) создает вокруг себя «тоннель» из магнитного поля. Стенки этого «тоннеля» «плотнее» вблизи движущего заряда. Чем дальше от движущегося заряда, тем слабее напряженность («сила») создаваемого им магнитного поля. Тем слабее реагирует на это поле стрелка компаса.

Закономерность распределение напряженности магнитного поля вокруг его источника такая же, как закономерность распределения электрического поля вокруг заряженного тела – она обратно пропорциональна квадрату расстояния до источника поля.

Если положительно заряженный шарик перемещается по кругу, то кольца магнитных полей, образующихся вокруг него по мере его движения, суммируются, и мы получим магнитное поле, направленное перпендикулярно плоскости, в которой перемещается заряд:

Магнитный «тоннель» вокруг заряда оказывается свернутым в кольцо и напоминает по форме тор (бублик).

Такой же эффект получается, если свернуть в кольцо проводник с током. Проводник с током, свернутый в многовитковую катушку называется электромагнитом. Вокруг катушки складываются магнитные поля движущихся в ней заряженных частиц — электронов.

А если заряженный шарик вращать вокруг его оси, то у него появится магнитное поле, как у Земли, направленное вдоль оси вращения. В данном случае током, вызывающим появление магнитного поля, является круговое движение заряда вокруг оси шарика – круговой электрический ток.

Здесь, по сути, происходит то же самое, что и при движении шарика по кольцевой орбите. Только радиус этой орбиты уменьшен до радиуса самого шарика.

Все сказанное выше справедливо и для шарика заряженного отрицательно, но его магнитное поле будет направлено в противоположную сторону.

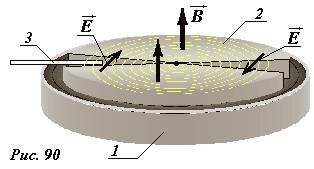
Данный эффект был обнаружен в опытах Роуланда и Эйхенвальда. Эти господа регистрировали магнитные поля вблизи вращающихся заряженных дисков: рядом с этими дисками начинала отклоняться стрелка компаса. Направления магнитных полей в зависимости от знака заряда дисков и направления их вращения, показаны на рисунке:

При вращении незаряженного диска, магнитные поля не обнаруживались. Не было магнитных полей и вблизи неподвижных заряженных дисков.

Модель магнитного поля движущегося заряда

Чтобы запомнить направление магнитного поля движущегося положительного заряда, мы представим себя на его месте. Поднимем правую руку вверх, затем укажем ею направо, затем опустим ее вниз, затем укажем влево и вернем руку в исходное положение – вверх. Затем повторим это движение. Наша рука описывает круги по часовой стрелке. Теперь начнем движение вперед, продолжая вращать рукой. Движение нашего тела – аналог движения положительного заряда, а вращение руки по часовой стрелке – аналог магнитного поля заряда.

Теперь представьте себе, что вокруг нас находится тонкая и прочная эластичная паутина, похожая на струны пространства, которые мы рисовали, создавая модель электрического поля.

Когда мы движемся сквозь эту трехмерную «паутину», из-за вращения руки, она, деформируясь, смещается по часовой стрелке, образуя подобие спирали, словно бы наматываясь в катушку вокруг заряда.

Сзади, за нами, «паутина» восстанавливает свою правильную структуру. Примерно так можно представлять себе магнитное поле положительного заряда, движущегося прямо.

А теперь попробуйте двигаться не прямо вперед, а по кругу, например, поворачивая при ходьбе налево, при этом вращая рукой по часовой стрелке. Представьте себе, что вы движетесь через нечто, напоминающее желе. Из-за вращения вашей руки, внутри круга, по которому вы движетесь, «желе» будет смещаться вверх, образуя горб над центром круга. А под центром круга, образуется впадина из-за того, что часть желе сместилось вверх. Так можно представлять себе формирование северного (горб сверху) и южного (впадина снизу) полюсов при движении заряда по кольцу или его вращения.

Если при ходьбе вы будете поворачивать направо, то «горб» (северный полюс) сформируется снизу.

Аналогично можно сформировать представление о магнитном поле движущегося отрицательного заряда. Только вращать рукой нужно в противоположную сторону – против часовой стрелки. Соответственно, магнитное поле будет направлено в противоположную сторону. Просто каждый раз следите за тем, в какой сторону ваша рука выталкивает «желе».

Такая модель наглядно демонстрирует то, почему северный полюс одного магнита притягивается к южному полюсу другого магнита: «горб» одного из магнитов втягивается во «впадину» второго магнита.

И еще эта модель показывает, почему не существуют отдельных северных и южных полюсов магнитов, как бы мы их не разрезали – магнитное поле представляет собой вихревую (замкнутую) «деформацию пространства» вокруг траектории движущегося заряда.

У электрона было обнаружено магнитное поле, такое, какое у него должно быть в том случае, если бы он был шариком, вращающимся вокруг своей оси. Это магнитное поле назвали спином (от английского to spin — вращаться).

Кроме того, у электрона существует еще и орбитальный магнитный момент. Ведь электрон не только «вращается», но движется по орбите вокруг ядра атома. А движение заряженного тела порождает магнитное поле. Так как электрон заряжен отрицательно, магнитное поле, вызванное его движением по орбите, будет выглядеть так:

Если направление магнитного поля, вызванного движением электрона по орбите, совпадает с направлением магнитного поля самого электрона (его спином), эти поля складываются и усиливаются. Если же эти магнитные поля направлены в разные стороны, они вычитаются и ослабляют друг друга.

Кроме того, могут суммироваться или вычитаться друг из друга магнитные поля других электронов атома. Этим объясняется наличие или отсутствие магнетизма (реакции на внешнее магнитное поле или наличие собственного магнитного поля) некоторых веществ.

Эта статья — отрывок из книги об азах химии. Сама книга здесь:
sites.google.com/site/kontrudar13/himia

UPD: Материал предназначен, в первую очередь, для школьников средних классов. Возможно, Хабр не место для подобных вещей, Но где место? Нет его.

Источник

Учебники

Журнал «Квант»

Общие

§14. Движение заряженных частиц в электрическом и магнитном полях

14.2 Плоское движение заряженной частицы в однородном магнитном поле.

При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы.

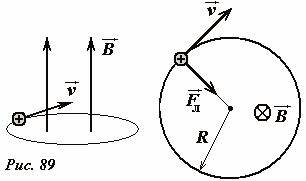
Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля (Рис. 89). Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля \(

\vec B\), то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным F_л = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона

из которого находим

Найдем период обращения частицы в магнитном поле

Из этой формулы следует интересный и неожиданный вывод [1] – период вращения частицы в магнитном поле не зависит от ее скорости. Частота вращения выражается формулой

и называется циклотронной частотой.

14.2.1 Циклотрон.

Постоянство частоты вращения частиц в магнитном поле используется в циклотроне одном из типов ускорителей заряженных частиц – ионов.

Ускорители подобного типа были разработаны и построены в 30-х годах ХХ века и сыграли (и продолжают играть) большую роль в развитии ядерной физики. Не смотря на простоту основных принципов работы ускорителя, циклотрон является очень сложным инженерным сооружением, включающим (помимо описанных элементов) источники питания (электромагнитов, источников частиц, ускоряющей системы, системы регистрации и д.р.), вакуумную систему, блоки управления и регистрации и т.д.

14.2.2 Масс-спектроскопия.

Характеристики движения частиц в магнитном поле (радиус траектории, время движения) зависят от их масс и зарядов. Изучение движения частиц в магнитных полях является основой масс-спектроскопии – метода исследования вещества по спектру [3] масс атомов и молекул, входящих в его состав. Сущность метода состоит в том, что ионизованные атомы и молекулы, проходя через магнитное поле, пространственно разделяются и регистрируются в различных точках. Первоначальными задачами масс-спектроскопии были исследование изотопного состава элементов и прецизионное (точное) измерение масс атомов. В дальнейшем масс-спектроскопия выросла в универсальный аналитический метод, применяющийся в экспериментальной физике, химии, биологии, геологии, технике. Приборы, позволяющие разделять и регистрировать частицы, называются масс-спектрометрами.

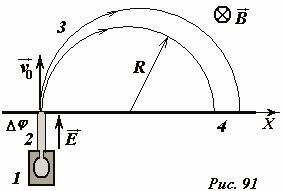
Принцип действия масс-спектрометра показан на рис. 91. Исследуемый образец специальными методами (испарением, электронным ударом) переводится в газообразное состояние, затем образовавшийся газ ионизируется в источнике 1. Затем ионы ускоряются электрическим полем и формируются в узкий пучок в ускоряющем устройстве 2 и через узкую входную щель 3 попадают в камеру 4, в которой создано однородное поперечное магнитное поле. В камере ионы движутся по дуге окружности и попадают на экран 5, где регистрируется место их попадания. Методы регистрации могут быть различными – фотографические, электронные и т.д. Радиус траектории зависит от массы и заряда иона, поэтому разные ионы попадают на экран на различном расстоянии от источника, что и позволяет их разделять и анализировать состав образца.

Найдем координату точки попадания иона на экран в зависимости от его массы, заряда и параметров прибора. В ускоряющем устройстве, пройдя разность потенциалов Δϕ, приобретают скорость υ₀, которая может быть найдена из уравнения закона сохранения энергии

из которого следует

Начальной скоростью ионов можно пренебречь, так как обычно она значительно меньше скорости после ускорения. Кроме того, в некоторых приборах применяют дополнительные устройства для выделения частиц имеющих близкие значения скоростей. В магнитном поле ионы движутся по окружности радиуса

которая зависит от отношения массы к заряду частицы. Координата попадания иона на экран равна диаметру окружности

В большинстве случаев ионы являются однозарядными (т.е. атомы и молекулы в процессе ионизации теряют один электрон), поэтому фактически прибор разделяет ионы по их массе, формируя масс-спектр исследуемого образца. Если в исходном образце присутствуют различные ионы, то на экране образуется несколько полос, координаты которых позволяют определить состав исходной смеси. Одной из важнейших характеристик масс-спектрометров является их разрешающая способность – характеристика, указывающая, при какой минимальной разности масс, ионы могут различены. Разрешающая способность прибора ограничена, так как полосы на экране не являются абсолютно тонкими, они всегда несколько размыты, имеют некоторую ширину. Если разность координат полос, соответствующих ионам мало различающихся масс (например изотопам одного химического элемента), оказывается меньше ширины полос, то эти полосы сольются, что сделает невозможным разделение (разрешение) двух типов ионов. Кроме того, ширина образующейся полосы Δx определяет погрешность определения массы иона.

Из формулы (4) следует, что масса иона рассчитывается по формуле

Если считать, что основную погрешность в определение массы вносит погрешность определения координаты полосы (то есть ее ширина) Δx, то погрешность определения массы следует рассчитывать по формуле

а относительная погрешность равна

Таким образом, уменьшение ширины образующейся полосы является одной из важнейших задач разработчиков масс-спектрометров.

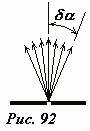
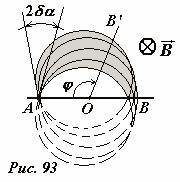
Не случайно в рассматриваемом приборе ионы пролетают половину окружности (их угол поворота равен π) – в этом случае однородное поперечное поле частично фокусирует ионы на регистрирующем экране. Рис. 93 иллюстрирует фокусировку пучка частиц в однородном поперечном магнитном поле. В идеальном случае, когда все частицы вылетают строго в одном направлении, нет необходимости заставлять ионы пролетать половину окружности. В принципе, экран OB’ можно расположить под произвольным углом ϕ. Однако, если ионы вылетают из щели A в пределах некоторого угла 2δα, то пучок ионов (на рис. 93 заштрихован) обладает некоторой шириной, причем его ширина минимальна именно при угле поворота ионов равному π. Найдем эту минимальную ширину пучка, которая равна ширине полосы на экране AB.

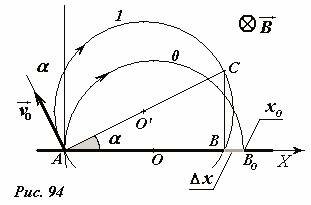
Пусть ион влетает в область магнитного поля под углом α к нормали (Рис. 94) и затем движется по дуге окружности ACB. Для сравнения на рисунке изображена «идеальная» траектория AB₀ частицы, влетевшей перпендикулярно экрану. Если вектор начальной скорости частицы \(

Эта координата максимальна для «идеальной» траектории α = 0 и уменьшается при увеличении угла отклонения вектора начальной скорости, причем не зависимо от того в какую сторону. Если максимальный угол отклонения равен δα, то ширина полосы равна

при малом δα следует воспользоваться приближенной формулой \(

а относительное уширение полосы оказывается равным

Как следует из полученного результата, уширение полосы является малой величиной более высокой степени (действительно (δα) 2 14.2.3 Магнитная отклоняющая система.

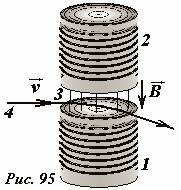
Магнитное поле также используется для отклонения пучков частиц. Причем магнитные отклоняющие системы электронных пучков в телевизионных трубках (кинескопах) и осциллографах используются гораздо чаще электростатических. Магнитная отклоняющая система проста – состоит из двух электромагнитов 1-2, в зазоре 3 которых проходит электронный пучок 4 (Рис. 95).

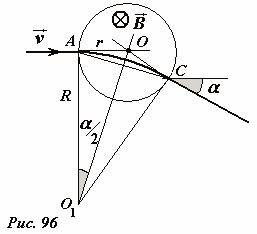
Найдем угол отклонения электронного луча в этом случае. Пусть область, занятая однородным магнитным полем индукции \(

\vec B\) (зазор между торцами магнитов, магнитным полем вне этой области можно пренебречь) имеет форму цилиндра радиуса r (Рис. 96). Для простоты будем считать, что пучок электронов движется по направлению к центру этой области и попадает в нее в точке A. Под действием магнитного поля пучок отклоняется и движется по дуге окружности AC, радиус которой равен

угол отклонения луча α легко находится из рисунка. Из прямоугольного треугольника AOO₁ следует, что

При малых углах (когда тангенс приблизительно равен самому углу) отклонение пропорционально индукции поля, которая в свою очередь пропорциональна силе тока электромагнита. Изменяя величину этого тока можно регулировать направление пучка электронов.

Источник

5.3. Движение заряда в однородном магнитном поле

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

из которого легко получить выражение для угловой скорости частицы

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

Кинетическая энергия протона будет

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).

Источник