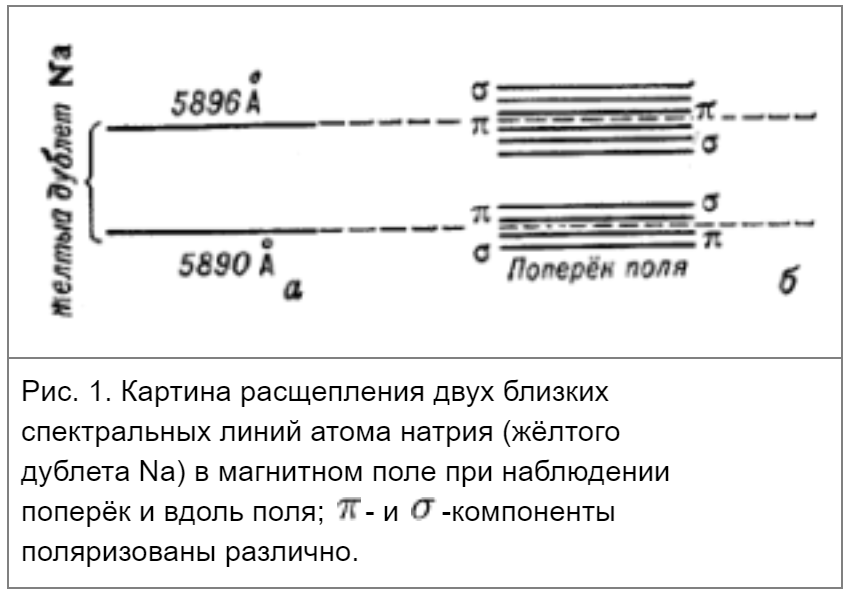
расщепление спектральных линий в магнитном поле

Эффекты Зеемана

Эффект Зеемана представляет собой явление расщепления спектральных линий в результате воздействия на излучающее вещество внешнего магнитного поля. Наблюдаемый в спектрах поглощения эффект Зеемана называется обратным. Все его закономерности аналогичны закономерностям в прямом эффекте, происходящем в линиях излучения.

Рассматриваемое явление было в 1896 году открыто нидерландским физиком П. Зееманом в процессе лабораторных исследований, относящихся к свечению паров натрия.

Распределение интенсивности в наблюдаемой системе компонентов становится сложным.

Первым ученым, объясняющим эффект Зеемана был нидерландский физик Х. Лоренц. Сделал это ученый в 1897 году в рамках классической теории, согласно которой движение электрона в атоме определяется в виде гармонии, то есть колебания линейного осциллятора. Согласно данной теории спектральная линия в условиях поперечного эффекта Зеемана расщепляется на три компонента. Такое явление было названо нормальным эффектом Зеемана, расщепление же линии на большее число компонентов определили как аномальное эффект Зеемана.

Однако, в большей части случаев наблюдается как раз аномальный эффект. Исключением могут считаться переходы между синглетными уровнями, а кроме них случаи сильного магнитного поля (смотрите ниже).

Полное объяснение эффекта Зеемана было получено на основе квантовой теории. Уровни энергии атома в магнитном поле претерпевают процесс расщепления на подуровни. Квантовые переходы между подуровнями пары уровней формируют компоненты спектральной линии. Механический момент количества движения J характеризует любой из энергетических уровней атома. Расщепление уровней основывается на том факте, что механический и магнитный моменты связаны друг с другом.

Механический момент атома суммируется из орбитального момента L и спинового момента S :

На рисунке 3 проиллюстрированы примеры зеемановского расщепления некоторых уровней.

Источник

Эффект Зеемана

Прямой (обращенный) эффект Зеемана состоит в расщеплении спектральных линий испускаемого (поглощаемого) излучения, если испускающие (поглощающее) вещество находится в магнитном поле. Эффект Зеемана обусловлен расщеплением энергетических уровней атомов или молекул в магнитном поле.

Эффект влияния магнитного поля на излучение атомов, обнаружен в 1896 г. голландским ученым Питером Зееманом и позднее теоретически был объяснен Хендриком Лоренцом.

Суть данного явления заключается в том, что в магнитном поле в результате действия сил Лоренца на вращающиеся вокруг ядра атома электроны происходит расщепление излучения атомов, в результате чего появляются две боковые частоты.

Рис. 5.4 Спектр излучения (поглощения) веществ в магнитном поле.

, (5.1)

(5.2)лияние магнитного поля на излучение атомов.

Полное объяснение эффекта Зеемана даёт квантовая теория.

Эффект Зеемана наблюдается и в молекулярных спектрах, однако расшифровать такие спектры значительно труднее, чем атомные. Кроме того, наблюдение эффекта в молекулярных спектрах представляет большие экспериментальные трудности из-за сложности картины расщепления и перекрытия молекулярных спектральных полос. Данный эффект можно наблюдать также и в спектрах кристаллов (обычно в спектрах поглощения).

Эффект Зеемана применяется не только в спектроскопии для исследования тонкой структуры вещества, но и в устройствах квантовой электроники, для измерения магнитных полей в лабораторных условиях, а также магнитных полей космических объектов.

Этот эффект сыграл важную роль в развитии атомной теории. Он показал, что испускание света атомом связано с движением его электронов, а позднее дал возможность детально и с высокой точностью проверить правильность квантовой механики – основы современной атомной теории.

В 1862, полагая, что магнитное поле должно влиять не только на распространение света, но и на его испускание, Фарадей исследовал спектр желтого света пламени, содержащего пары натрия, помещенного между полюсами магнита, но не обнаружил ожидаемого эффекта. Однако в 1896 голландский физик П. Зееман (1865–1943), работавший в Лейдене, повторил его попытку, применив более совершенный метод. Он обнаружил, что при наложении поля каждая из линий желтого дублета спектра натрия (так называемых D-линий) уширяется (т.е. увеличивается полоса испускаемых частот).

Теоретическое объяснение явления было дано соотечественником Зеемана, теоретиком Х. Лоренцом. Суть его рассуждений можно кратко изложить, рассматривая простые случаи. Допустим сначала, что заряд е движется в излучающем атоме по окружности, плоскость которой перпендикулярна магнитному полю В. Для простоты предположим, что сила, связывающая заряд с атомом, пропорциональна расстоянию r от центра окружности. (Это предположение не имеет принципиального значения, но упрощает вычисления.) В отсутствие поля В, приравняв центробежную силу инерции центростремительной силе, получим

откуда находим частоту обращения заряда:

Если наложено поле В, то оно действует на заряд с силой evB, заставляющей его двигаться из плоскости рисунка. При этом полная сила, действующая на заряд, равна mv2/r + evB; следовательно,

Эффект можно наблюдать с помощью спектроскопа, установленного в положение D1 или D2, если заряд излучает, двигаясь по окружности, между северным и южным полюсами магнита.

Приближенное решение этого уравнения, справедливое при всех значениях индукции В, кроме экстремальных, имеет вид

-1560(4) vчас = v0 – eB/4m,

где индекс «час» указывает на то, что вращение, наблюдаемое с позиции D2, происходит по часовой стрелке. Если бы заряд вращался против часовой стрелки, то действие поля B было бы противоположным и

Наконец, если плоскость вращения параллельна магнитному полю, то последнее не влияет на частоту обращения.

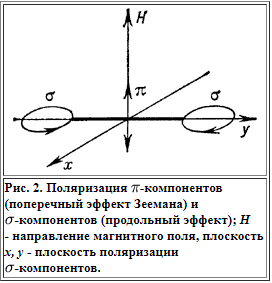
Рассмотрим теперь нагретый до свечения газ, в котором имеются все три типа движущихся по орбитам электронов, а также промежуточные ориентации. Предположим, что спектроскоп расположен в точке D1. Орбитам с движением электронов по часовой стрелке и против часовой стрелки будет соответствовать плоско-поляризованный свет с частотами vчас и vпротив. Если плоскость орбиты совпадает с направлением поля, то частота света останется неизменной. Таким образом, будут наблюдаться три спектральные линии. Если просверлить отверстие в полюсном наконечнике магнита, то можно наблюдать свет в направлении D2. Проведенный выше анализ показывает, что в этом направлении можно наблюдать две компоненты – циркулярно-поляризованные по часовой стрелке и против часовой стрелки, с частотами vчас и vпротив. Первые грубые измерения подтвердили эти теоретические предсказания. Зееман обнаружил, что vпротив меньше vчас. Согласно формулам (4) и (5), это свидетельствует о том, что вращаются отрицательные заряды, а на основании измеренного уширения исходной линии Зееман сделал вывод, что отношение заряда частицы к ее массе составляет примерно Кл/кг. За несколько лет до этого Дж. Томсон, изучая процессы в газоразрядных трубках, обнаружил частицы, позднее названные электронами, и установил наличие у них отрицательного заряда, причем отношение их заряда к массе составляло Кл/кг. Поскольку, кроме электрона, не существует других частиц с близкими значениями отношения заряда к массе, именно электроны (хотя они и составляют ничтожную долю массы всего атома) ответственны за испускание света. Это чрезвычайно важное открытие подготовило почву для разработки теории электронного строения атомов, которая, начиная с вклада Резерфорда и Бора в 1911 и 1912, развивалась, превратившись в современную общепризнанную теорию атома. Но как только было осознано важность значения открытия Зеемана, стали возникать трудности. В 1898 Т. Престон сообщил о том, что некоторые спектральные линии цинка и кадмия расщепляются на четыре компоненты, а вскоре А.Корню обнаружил, что из двух D-линий натрия, с которыми экспериментировали Фарадей и Зееман, одна расщепляется на четыре, а другая – на шесть компонент. В 1911 К. Рунге и Ф. Пашен установили, что интенсивная зеленая линия в спектре ртути расщепляется на 11 компонент. Сначала столь сильное расщепление было воспринято как «аномальный эффект Зеемана». Но вскоре стало ясно, что «нормальный эффект Зеемана» с расщеплением на три компоненты сам представляет собой исключение, и возникла необходимость в дальнейшем уточнении теории Лоренца.

А.Ланде из Тюбингена нашел в 1923 (проанализировав экспериментальные данные для большого числа частных случаев) сложную общую формулу, которая позволяла точно рассчитать эффект Зеемана для любой спектральной линии. Причина, по которой для описания простых явлений, возникающих при движении атомного электрона в магнитном поле, необходима столь сложная формула, стала ясна после открытия, сделанного в 1925 С. Гаудсмитом и Дж. Уленбеком. Они обнаружили, что электрон ведет себя наподобие волчка, вращаясь вокруг собственной оси. Электродинамика показывает, что такой электрон должен вести себя как маленький магнит и что именно двойное взаимодействие с магнитным полем орбитального момента в атоме и спина приводит к сложной динамической картине.

В 1926 В. Гейзенберг и П. Иордан, пользуясь методами квантовой механики, проанализировали эффект Зеемана и вывели формулу Ланде из основных принципов теории. Это исчерпывающее объяснение эффекта Зеемана явилось одним из первых триумфов новой атомной теории. Современные научные методы позволяют использовать эффект Зеемана для идентификации атомных и ядерных состояний. Формулы типа формулы Ланде, связывающие зеемановское расщепление в спектрах атомов, молекул и ядер с их вращательным движением, позволяют по данным измерения эффекта Зеемана в спектрах, обусловленного неизвестными атомными конфигурациями, выяснять характер этих конфигураций. Эффект Зеемана обычно исследуют методами спектроскопии или методами атомных и молекулярных пучков.

В астрофизике эффект Зеемана используется для определения магнитных полей космических объектов.

Рис. 4. Нормальный эффект Зеемана;

стрелками обозначена поляризация
компонентов, — частота исходной
линии, и —
частоты -компонентов.

Источник

Атом в магнитном поле. Эффект Зеемана. Эффект Пашена-Бака

еВ

где со, — ларморовская частота прецессии, со, =- (Лармор, 1897).

К такому же результату приводит квантовая теория (Дебай, Зоммерфельд, 1916). Действительно, проекция магнитного момента, связанного с орбитальным движением электронов в атоме, на выделенное направление равна т₇р_Б, где т₁ — магнитное квантовое число; р_Б — магнетон Бора. Для атома, помешенного в магнитное поле, выделенным является направление магнитного поля. В этом поле атом, обладающий магнитным моментом, приобретает дополнительную энергию:

Отсюда видно, что каждый уровень энергии в магнитном поле расщепляется на 2/+ 1 подуровней. Таким образом, уровни энергии атома в магнитном поле определяются формулой:

Частота линии излучения (или поглощения), соответствующая переходу между двумя состояниями, равна

Для наблюдения эффекта Зеемана использовали установку, схема которой изображена на рис. 3.26. Между полюсами сильного электромагнита, создающего однородное магнитное поле, помещали источник линейчатого спектра И. Наблюдения проводили поперек и вдоль магнитного поля. Для этого в сердечнике просверлили специальный канал. Излучаемый свет фокусировался линзой L, (или L₂).

Характер поляризации света определяли с помощью анализатора N_<(N₂). Далее свет попадал в спектральный прибор П_± (П„) большой разрешающей силы. При наблюдении поперек магнитного поля для некоторых простых синглетных линий, например, ртути, кадмия идр. действительно обнаруживается лоренцевский триплет (3.85). При продольном же наблюдении возникает дублет, так как линия с частотой со₀ отсутствует.

Отметим, что эффект Зеемана наблюдается также и на линиях поглощения. Это называют обратным эффектом Зеемана.

Опыт показывает, что чаще всего наблюдается не лоренцевское расщепление, а более сложная картина, которую называют сложным, или аномальным, эффектом Зеемана. Впервые его наблюдали Престон и Корню (1897). Этот эффект никак не удавалось удовлетворительно объяснить до открытия спина электрона.

При теоретическом описании эффекта Зеемана надо определить оператор Гамильтона, который можно приближенно представить в виде:

Рассмотрим сначала случай слабого магнитного поля. Будем предполагать, что осуществляется нормальный тип связи атомных моментов. В рассматриваемом случае слабого магнитного поля спин-орбитальное взаимодействие, приводящее к тонкой структуре, является более сильным, чем взаимодействие по отдельности магнитного спинового и магнитного орбитального моментов атома с внешним магнитным полем. Тогда необходимо иметь дело с полным моментом импульса атома J = L+S и с полным магнитным моментом М = М^ + М^, где М_А, М^. — магнитные моменты, связанные с полным орбитальным и спиновым движениями соответственно. Во внешнем магнитном поле атом приобретает дополнительную энергию

где черта сверху означает среднее значение в состояниях с заданными квантовыми числами У, L, S и различными числами т_г Если бы полный магнитный момент атома М был параллелен полному механическому моменту J, то из (3.88), как и из (3.86), (3.87), следовало бы, что происходит лоренневское расщепление спектральной линии. Однако это не так, что и является причиной аномального эффекта Зеемана. В самом деле магнитные орбитальный и спиновый моменты связаны с соответствующими механическими моментами соотношениями:

На рис. 3.29 изображено построение векторов J и М по их составляющим векторам. Отсюда видно, что векторы J и М не параллельны друг другу. При наличии спин-орбитального взаимодействия сохраняются длины |b|, |s| векторов L, S, а также длина вектора J и его проекция на направление магнитного поля. При этом векторы L, S быстро прецессируют вокруг полного момента J. Вместе с ними прецессируют также векторы М_?, М₅ и, следовательно, вектор магнитного момента М. Таким образом, вектор М имеет составляющую М_|( вдоль вектора J и составляющую М _L, перпендикулярную ему:

Вследствие прецессии вектора М вокруг вектора J составляющая М_± быстро вращается, поэтому ее среднее значение по времени равно нулю, а составляющая М_|( не изменяется. Другими словами, среднее значение магнитного момента равно:

где Мц = |Мц| — величина (модуль) вектора М_|(.

Таким образом, дополнительная энергия атома в магнитном поле (3.88) равна:

Вычислим проекцию М_|г Согласно определениям: Из рис. 3.29 видно, что

Следовательно, продольная составляющая магнитного момента равна:

Здесь введена постоянная:

Эта постоянная называется фактором, или множителем, Ланде. Если считать, что магнитное поле В направлено вдоль оси г, то из (3.92), (3.93) следует формула для дополнительной энергии атома в магнитном поле:

Таким образом, согласно (3.95) в слабом магнитном поле каждый уровень энергии атома расщепляется на 2У + 1 подуровней. При заданных квантовых числах фактор Ланде для разных термов может быть заранее рассчитан:

Расщепление в слабом магнитном поле спектральной линии, соответствующей переходу между состояниями «1» и «2», определяется формулой

при этом возможность переходов ограничивается, в общем, правилами отбора: АУ = 0, ± 1; А/и_у =0, ± 1; AL = 0, ± 1.

образом, в сильном магнитном поле наблюдается простой лоренцевский триплет. Это явление, впервые обнаруженное Пашеном и Баком в 1912 г., называется эффектом Пашена- Бака, или магнитооптическим превращением, поскольку с увеличением магнитного поля аномальное зеемановское расщепление превращается в лоренцевский триплет. Очевидно, что в синглетах всегда должно наблюдаться простое зеемановское расщепление, поскольку в них отсутствует тонкая

структура. Поэтому для них любое магнитное поле является «сильным». В качестве примера на рис. 3.33 изображена схема расщепления термов 2 Р и 2 S в слабом (а) и сильном (б) магнитных полях.

Отметим, что при рассмотрении зеемановского расщепления уровней энергии совершенно не учитывалась их сверхтонкая структура, которая обусловлена спином ядра. Взаимодействие ядерного магнитного момента с внутриатомным магнитным полем, вызванным движениями электронов, приводит к тому, что каждый уровень энергии с определенным значением квантового числа У расщепляется на несколько подуровней. Если внешнее магнитное поле настолько слабое, что вызываемое им расщепление уровней энергии много меньше интервалов между уровнями сверхтонкой структуры, то картина зеемановского расщепления еше более усложняется.

Наличие у нейтральных атомов магнитного момента дает возможность воздействовать на них внешними магнитными полями. Это используют для сортировки и фокусировки пучка атомов, их удержания в некотором объеме с помощью специально подобранной конфигурации магнитного поля и т. д. Такие устройства называют магнитными ловушками для атомов.

1. В классической модели электрона, совершающего в атоме малые колебания с частотой со₀, рассчитать эффект Зеемана.

Решение. Помимо квазиупругой силы = -т_есо„г на электрон в

магнитном поле действует сила Лоренца = —e[v х в]. Пусть В = (0, 0, В).

Уравнения движения электрона:

Решение уравнений (1), (2) ищется в виде x(t) = ac

Из уравнения (3) видно, что вдоль магнитного поля колебания линейно поляризованы и частота их не изменяется.

2. Найти значение магнитного момента атома водорода в основном состоянии.

Решение. Согласно формуле (3.93), среднее значение магнитного момента атома с учетом спин-орбитального взаимодействия равно

3. Определить значение магнитного момента атома в состоянии 3 /)₂ и его проекции на направление внешнего магнитного поля.

4. Определить критическое значение магнитного поля для резонансного дублета, например, цезия (X, =8521 10

8 см, Х₂ =8943-10 8 см).

Решение. Для первого состояния фактор =4/5, для второго — g₂ = 2/3. Уровень 2 Dy₂ расщепляется на4 подуровня по/я_у,ауровень 2р 1/2- на два. С учетом правила отбора Д/л_у =0, ±1 находим зеемановское расщепление (6 компонент): Дсо = со_А

Источник

Расщепление спектральных линий в магнитном поле

Простой эффект Зеемана

Величина расщепления пропорциональна Н и относительно мала (для Н

20 кЭ она порядка десятых долей ангстрема). В сильных магнитных полях (полях, вызывающих расщепление порядка мультиплетного и выше) вместо сложного Зеемана эффекта наблюдается зеемановский триплет (Пашена-Бака эффект).

При этом значения De = g m Б H m для разных m различны.

Расстояние между соседними подуровнями:

Исследование картины зеемановского расщепления важно для изучения тонкой структуры атомов и других атомных систем. Наряду с квантовыми переходами между зеемановкими подуровнями, принадлежащими различным уровням энергии (Зеемана эффект на спектральных линях), можно наблюдать магнитные квантовые переходы между подуровнями одного уровня энергии. Такие переходы происходят под действием излучения с частотами:

Зеемана эффект наблюдается в молекулярных спектрах, однако его наблюдение и расшифровка представляют большие трудности вследствие сложной картины расщепления и перекрытия в них спектральных полос. Зеемана эффект можно наблюдать в спектрах кристаллов (обычно в спектрах поглощения).

Технические реализации эффекта

Техническая реализация Зеемана эффекта

Наблюдение эффекта Зеемана осуществляется, как правило, по спектру поглощения света в изотропном веществе в присутствии магнитного поля. Схема соответствующей установки представлена на рис. 2.

Схема наблюдения эффекта Зеемана

Зеемана эффект применяется в спектроскопии и в устройствах квантовой электроники, в частности, для измерения напряженностей слабых магнитных полей в лабораторных условиях и в космосе.

1. Физика. Большой энциклопедический словарь.- М.: Большая Российская энциклопедия, 1999.- C.90, 460.

2. Новый политехнический словарь.- М.: Большая Российская энциклопедия, 2000.- C.20, 231, 460.

Источник

• ← Слова со словом скидка
• Решетки на окна распродажа →