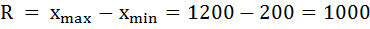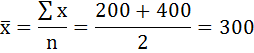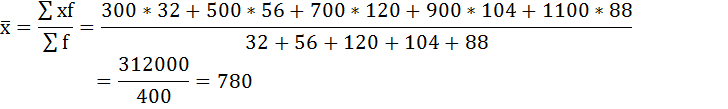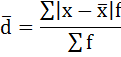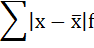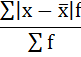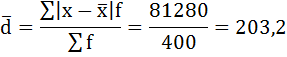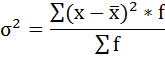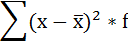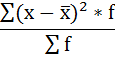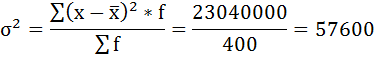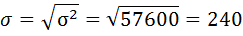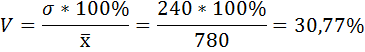Размах вариации курса акций
Как считать индикаторы инвестиционной привлекательности активов
На примере портфеля Уоррена Баффетта
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
((1 + 20%) × (1 − 10%) × (1 + 30%)) 1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному : акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%) 1/4 = 15,8%.
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%) 1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность) (365 / Количество дней владения активом) − 1
(1 + 74%) (365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива) (1 / Количество периодов) − 1
((270 × 20 + 2 × 20) / 200 × 20) (1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как победить выгорание
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Правило трех сигм гласит, что практически все значения нормально распределенной случайной величины лежат в диапазоне трех стандартных отклонений от среднего арифметического значения случайной величины. Случайной величиной у нас выступает годовая доходность по акции
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
Экспресс-подготовка к онлайн-тестированию:
для студентов дистанционного обучения, при устройстве на работу, прохождении аттестаций
Сдаешь тесты самостоятельно?
Закажи скайп-консультацию и узнай все секреты успешной сдачи экзаменов онлайн!
Статистика МФПА Тест с ответами
Правильных ответов не менее 97%
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
В Российской Федерации основные вопросы организации статистического учета регулируются …
Правительством Российской Федерации
+Федеральным законом «Об официальном статистическом учете и системе государственной статистики в Российской Федерации»
Президентом Российской Федерации
Данные об организациях, созданных на территории РФ, их местных единицах, индивидуальных предпринимателях, других типах статистических единиц, являющихся объектами федерального статистического наблюдения, отражаются Росстатом …
в статистических отчетах
+ в Статистическом регистре хозяйствующих субъектов
в статистических публикациях
Объектом статистики является изучение …
взаимосвязи между социально-экономическими явлениями посредством статистических показателей
количественной стороны массовых социально-экономических явлений и процессов
Медианой распределения является …
значение изучаемого признака, повторяющееся с наибольшей частотой
разность между наибольшим и наименьшим значениями варьирующего признака
+ значение признака, приходящееся на середину ранжированной совокупности
При сравнении всех уровней ряда динамики с первым уровнем рассчитанные показатели называют …
Основанием группировки может быть … признак
+как качественный, так и количественный
Наибольшее значение признака в интервале называется … границей
Для прогнозирования величины колебания курса доллара на основании изменения цены барреля нефти следует применить … анализ
Признаки, изменяющиеся под воздействием других связанных с ними признаков, называются …
Если число уровней ряда – четное, то показатель времени t методом условного нуля задается как …
Показатель «Отношение затрат на оплату труда топ-менеджеров предприятия к объему затрат на основной персонал предприятия» является примером относительного показателя …
реализации планового задания
Показатель «Курс рубля по отношению к доллару» является примером относительного показателя …
Расчет среднегодовой численности предприятий по данным за 2007–2013 гг. (на 1 января каждого года) следует производить по формуле средней …
2007 2008 2009 2010 2011 2012 2013
2901 3106 3346 3594 3845 4150 4417
Если объем инвестиционных вложений характеризуется следующим рядом динамики, млн руб. по месяцам 2013 г. (см. таблицу), то средний абсолютный прирост объема инвестирования за последние 3 месяца составляет …
Январь Февраль Март Апрель Май Июнь Июль
90,0 92,0 80,0 78,0 86,0 60,0 80,0
Если для исследования соблюдения регламента взаимодействия с клиентами персоналом торгово-сбытовой компании строится 15-процентная выборка, объектами которой становятся сотрудники по работе с клиентами торговых точек компании, отбираемых пропорционально количеству сотрудников компании в соответствующем федеральном округе РФ, то такое построение выборки характерно для …
систематической (механической) выборки
собственно случайной выборки
повторной выборки любого вида выборочного исследования
+стратифицированной (типической) выборки
Если среднемесячная номинальная начисленная заработная плата работников в Российской Федерации в 2011 году составляла 23369,2 руб., то в этом случае с точки зрения статистических категорий показателем является …
среднемесячная номинальная начисленная заработная плата
Если относительный показатель реализации предприятием плана производства продукции составил 103 %, а объем производства по сравнению с предшествующим периодом вырос на 2 %, значит, план предусматривал … объема производства
В представленном ряду распределения (см. таблицу) модальным является интервал …
Выручка аудиторской фирмы
За I полугодие 2013 года, млн. руб. Число фирм
Размах вариации группировочного признака определяется по формуле …
Статистическая совокупность, все единицы которой близки друг к другу по значениям выбранных для исследования признаков, в статистике называется …
При построении интервальной группировки из 6 групп с минимальным значением группировочного признака, равным 130, и максимальным, равным 250, ширина равного интервала составит …
Если зависимость стоимости рекламного объявления (Y, руб.) от численности читательской аудитории (Х, тыс. чел.) описывается уравнением Yх = 1300 + 5Х и численность аудитории достигнет 10 тыс. чел., то стоимость рекламного объявления составит …
Если в совокупности единиц среднее квадратическое отклонение признака составило 7, а средняя величина этого признака равняется 21, то совокупность единиц по величине данного признака …
Среднее квадратическое отклонение можно рассчитать по формуле …
Абсолютные показатели отображают …
соотношение значений индивидуальных показателей
разницу между значениями индивидуальных показателей
+размеры и характеристики индивидуальных объектов
Темп роста исчисляется как … уровней ряда
Данные приведенной ниже таблицы представляют собой пример … ряда распределения
Распределение акций по величине курса продажи
Курс акции, руб. Число акций
При уменьшении объема выборки величина ее средней ошибки …
При анализе товарооборота супермаркета сводный индекс цен продукции составил 104,5 %. – следовательно, стоимость продукции …
увеличилась на 104,5 %
Если менеджер по персоналу для исследования показателей квартальной производительности труда менеджеров по работе с физическими лицами корпорации извлек систематическую выборку объемом 30 человек из 150 менеджеров, состоящих в штате, то доля отбора составленной им выборки равна …
При функциональной зависимости между Х и Y значение коэффициента корреляции …
Под вариацией понимают изменение …
массовых явлений во времени
состава объектов статистической совокупности
+значений признака у различных единиц совокупности
Расчет средней величины по указанным данным (см. таблицу) следует производить по формуле средней …
Выручка ауд. фирмы Средняя стоимость контракта Федеральный округ
за I пол 2013 г., млн. р. на проведение аудита, млн. р.
Если товарооборот в целом по товарной группе в июне составил 900 тыс. руб., а в мае (при фиксированном объеме реализации на уровне июня) – 850 тыс. руб., это говорит о величине …
+ перерасхода покупателей на 50 тыс. руб. от изменения цен
экономии покупателей на 50 тыс. руб. от изменения себестоимости
перерасхода покупателей на 800 тыс. руб. от изменения цен
Характеристика выборочной совокупности, зависящая от уровня вероятности, с которым гарантируется, что средняя величина признака в генеральной совокупности не выйдет за рассчитанные границы, – это …
+предельная ошибка выборки
средняя ошибка выборки
Чтобы получить относительный показатель динамики с переменной базой сравнения для i-го периода, необходимо …
+разделить значение показателя в i-й период на величину показателя в предшествующий i-му период
разделить значение показателя в период i на значение, соответствующее начальному периоду рассматриваемого ряда динамики
разделить значение показателя в период (i – 1) на значение показателя в период i
числитель исходного соотношения средней величины неизвестен
знаменатель исходного соотношения средней величины известен
+знаменатель исходного соотношения средней величины неизвестен
Единица наблюдения – это
+первичный элемент статистической совокупности, являющийся носителем признаков
элемент математического множества
Отдельное значение группировочного признака, положенного в основание ряда распределена, называют.
числитель исходного соотношения средней величины неизвестен
знаменатель исходного соотношения средней величины известен
+знаменатель исходного соотношения средней величины неизвестен
Структурными средними являются …
Если использовать коэффициент вариации для оценки однородности земельных участков по урожайности
Участок Урожайность, ц/га Посевная площадь, га
то доля участков указанных в ряду распределения будет составлять
произведение уровней ряда
+разность уровней ряда
отношение уровней ряда
+при которой, определенному значению факторного признака соответствует одно значение результативного
между двумя признаками
при которой, определенному значению факторного признака соответствует несколько значений результативного
Коэффициент вариации характеризует:
пределы колеблемости признака
тесноту связи между признаками
диапазон вариации признака
+степень вариации признака
Аналитическое выражение связи определяется с помощью метода анализа
Коэффициент вариации признака составил 25%, средняя величина признака – 25. определите среднее квадратическое отклонение признака:
+среднее квадратическое отклонение
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Определите:
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | 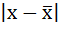 | 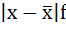 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | 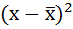 | 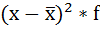 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.