сформировать и визуализировать сигналы заданной формы матлаб
Документация
В этом примере показано, как визуализировать и измерить сигналы во время и частотный диапазон в MATLAB® с помощью осциллографа времени и спектра анализатор.
Визуализация сигнала во временном и частотном диапазонах
Создайте синусоиду с частотой 100 Гц, произведенных на уровне 1 000 Гц. Сгенерируйте пять секунд синусоиды на 100 Гц с аддитивным 
белым шумом во вторых интервалах. Отправьте сигнал в осциллограф времени и спектр анализатор для отображения и измерения.
Измерения временного интервала
Используя осциллограф времени, можно сделать много измерений сигнала.
Следующие измерения доступны:
Можно включить и отключить эти измерения от вкладки Measurements.
Чтобы проиллюстрировать использование измерений в осциллографе времени, симулируйте сигнал ECG. Используйте ecg функция, чтобы сгенерировать 2 700 выборок сигнала. Используйте фильтр Savitzky-Golay, чтобы сглаживать сигнал и периодически расширять данные, чтобы получить приблизительно 11 периодов.
Отобразитесь сигнал во время определяют объем и используют Пиковые измерения Средства поиска и Data Cursor. Примите частоту дискретизации 4 кГц.
Включите Пиковые Измерения из вкладки Measurements путем нажатия соответствующей кнопки панели инструментов. Панель Peaks появляется в нижней части окна scope времени. Для свойства Num Peaks введите 8 и нажмите Enter. В панели Peaks осциллограф времени отображает список 8 пиковых амплитудных значений и времена, в которые они происходят.
Существует постоянная разница во времени 0,675 секунд между каждым heartbeat. Поэтому сердечный ритм сигнала ECG дан следующим уравнением:
Включите Измерения Курсора из вкладки Measurements путем нажатия соответствующей кнопки панели инструментов. Курсоры появляются на осциллографе времени с полем, показывающим изменение вовремя и значение между этими двумя курсорами. Можно перетащить курсоры и использовать их, чтобы измерить время между событиями в форме волны. Когда вы перетаскиваете курсор, время, значение в курсоре появляется. Этот рисунок показывает, как использовать курсоры, чтобы измерить временной интервал между peaks в форме волны ECG. 
Измерение в поле курсора демонстрирует, что временной интервал между двумя peaks составляет 0,675 секунды, соответствуя сердечному ритму 1,482 Гц или 88,9 ударам/min.
Статистика сигнала и двухуровневые измерения
Можно также выбрать Signal Statistics и различные двухуровневые измерения от вкладки Measurements. Статистика сигнала может использоваться, чтобы определить минимальные и максимальные значения сигнала, а также другие метрики как от пика к пику, среднее значение, медиана и значения RMS. Двухуровневые измерения могут использоваться, чтобы определить информацию о повышении и падающих переходах, аберрациях перехода, перерегулировании и информации об отклонении от номинала, времени урегулирования, ширине импульса и рабочем цикле. Чтобы читать больше об этих измерениях, смотрите, Конфигурируют Time Scope Объект MATLAB.
Измерения частотного диапазона
Этот раздел объясняет, как сделать измерения частотного диапазона со спектром анализатор.
Спектр анализатор обеспечивает следующие измерения:
Можно включить и отключить эти измерения от спектра панель инструментов анализатора или в меню Tools> Measurements.
Чтобы проиллюстрировать использование измерений со спектром анализатор, создайте синусоиду на 2,5 кГц, произведенную на уровне 48 кГц с аддитивным белым Гауссовым шумом. Оцените старший полином (9-я степень) в каждом значении сигналов, чтобы смоделировать нелинейное искажение. Отобразите сигнал в спектре анализатор.
Включите гармонические измерения искажения путем нажатия на соответствующий значок на панели инструментов или путем нажатия на пункт меню Tools> Measurements> Distortion Measurements. В Измерениях Искажения измените значение для Цифры. Гармоники к 9 и проверка флажок Label Harmonics. В панели вы видите значение основного принципа близко к 2 500 Гц и 8 гармоник, а также их ОСШ, SINAD, THD и значений SFDR, на которые ссылаются относительно основной выходной мощности.
Пиковое средство поиска
Можно отследить изменяющиеся во времени спектральные компоненты при помощи Пикового диалогового окна измерения Средства поиска. Можно показать и опционально пометить до 100 peaks. Можно вызвать Пиковое диалоговое окно Средства поиска от пункта меню Tools> Measurements> Peak Finder, или путем нажатия на соответствующий значок на панели инструментов.
Чтобы проиллюстрировать использование Пикового Средства поиска, создайте сигнал, состоящий из суммы трех синусоид с частотами 5, 15, и 25 кГц и амплитудами 1, 0.1, и 0.01 соответственно. Данные производятся на уровне 100 кГц. Добавьте 
белый Гауссов шум в сумму синусоид и отобразите односторонний спектр мощности в спектре анализатор.
Позвольте Пиковому Средству поиска пометить три частоты синусоиды. Значения частоты и степени в dBm отображены в Пиковой панели Средства поиска. Можно увеличить или сократить максимальное число peaks, задать минимальное пиковое расстояние и изменить другие настройки от панели Настроек в Пиковой панели Измерения Средства поиска.
Чтобы узнать больше об использовании измерений со спектром анализатор, смотрите Спектр пример Измерений Анализатора.
Открытый пример
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
Цифровая лаборатория FPGA / DSP
Информационно-учебный проект по цифровой электронике
ЛР3 > Сигналы и их свойства. Генерация сигналов в среде MatLab
Цель работы: научиться создавать различные типы сигналов и визуализировать их
Руководство по лабораторной работе
Для выполнения лабораторной работы Вам необходимо повторить соответствующие лекции.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
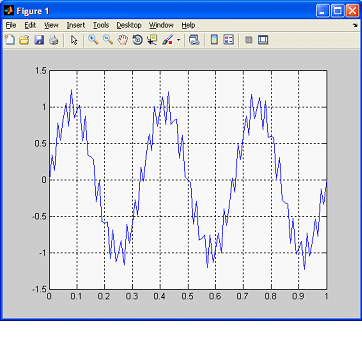
Гармонические сигналы и их комбинации в среде MatLab создаются с помощью функций Sin(x) и Cos(x). Следующий пример демонстрирует сигнал, представляющий собой сумму двух синусоид – 3Гц с амплитудой 1 В и 40 Гц с амплитудой 0,25 В. Сигнал сформирован для интервала времени от 0 до 1 с, частота дискретизации – 100 Гц.
Пример № 1
fs = 100; %частота дискретизации 100 Гц
t = 0:1/fs:1; %интервал времени от 0 до 1 сек
Результат работы программы представлен на рисунке 1.
Рисунок 1. Результат работы программы из примера № 1
Пример № 2
Fs = 8e3; %частота дискретизации 8 КГц
t = 0:1/Fs:1; %1 секунда дискретных моментов времени
t = t’; %преобразование строки в столбец
A = 2; %амплитуда – 2 В
f0 = 1e3; %частота – 1 КГц
phi = pi/4; %начальная фаза – 45 град
s1 = A*cos(2*pi*f0*t+phi); %гармонический сигнал
alpha = 1e3; %скорость затухания экспоненты
s2 = exp(-alpha*t).*s1; %затухающая синусоида
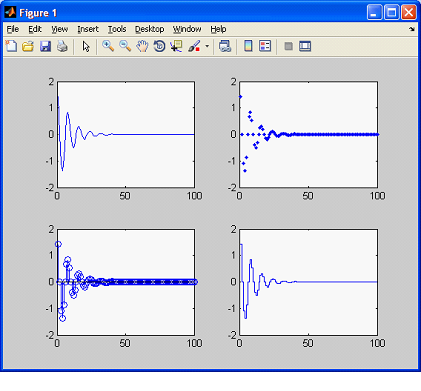
Результат работы программы представлен на рисунке 2.
Рисунок № 2. Результат работы программы из примера № 2
Для генерации одиночных импульсов в среде MatLab имеются встроенные функции:
rectpuls – прямоугольный импульс;
tripuls – треугольный импульс;
sinc – импульс вида sin(πt)/ (πt);
gausplus – радиоимпульс с гауссовой огибающей;
pulstran – последовательность из конечного числа импульсов произвольной формы.
Рассмотрим несколько примеров с использованием данных функций.
Функция rectpuls формирует одиночный прямоугольный импульс с единичной амплитудой. Формат вызова данной функции следующий:
y = rectpuls (t, width), где
t – вектор значений времени, width – ширина (длительность) импульса.
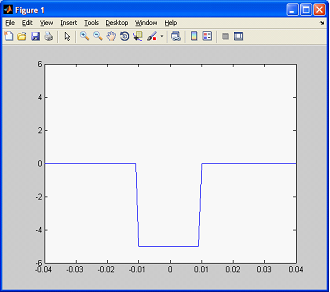
В качестве следующего примера рассмотрим генерацию одиночного отрицательного импульса, длительностью 20 мс и амплитудой – минус 5 В (пример № 3):
Пример № 3
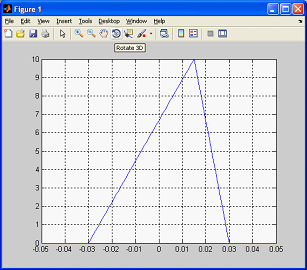
В качестве следующего примера рассмотрим генерацию одиночного треугольного импульса, длительностью 60 мс, амплитудой 10 В и смещением вершины на 15 мс (пример № 4).
Пример № 4
Fs = 1e3; %частота дискретизации
T1 = 0.5; %смещение вершины
T2 = 60e-3; %нижнее основание
s = A*tripuls(t,T2,T1);% генерация импульса
Функция gausplus формирует одиночный радиоимпульс с гауссовой огибающей и единичной амплитудой. Формат вызова данной функции следующий:
y = gauspuls(t, fc, bw, bwr), где
t – вектор значений времени, fc – несущая частота в Гц, bw – относительная ширина спектра (ширина спектра, деленная на несущую частоту), bwr – уровень (в децибелах), по которому производится измерение ширины спектра.
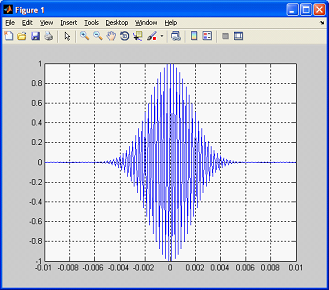
В качестве примера рассмотрим генерацию одиночного радиоимпульса с несущей частотой = 4 КГц, шириной спектра = 400 Гц, амплитудой = 1 В, уровнем измерения ширины спектра = – 20 дБ (пример № 5).
Пример № 5
Fs = 16e3;% частота дискретизации 16 КГц
Fc = 4e3;%несущая частота 4 КГц
bw = 0.1;%относительная ширина спектра 0.1
s=gauspuls(t,Fc,bw,bwr);% генерация радиоимпульса
Функция pulstran служит для генерации конечной последовательности импульсов одинаковой формы с произвольно задаваемыми задержками и уровнями. Формат вызова этой функции следующий:
y = pulstran(t, d, ‘func’, p1, p2, …), где
t – вектор значений времени, d – вектор задержек, ‘func’ – имя функции, генерирующей одиночный импульс (могут использоваться функции rectpuls,
tripuls, gausplus или собственные функции). Оставшиеся параметры p1, p2, … – дополнительные, они передаются функции ‘func’ при ее вызове.
ЗАДАНИЕ
Исследуйте самостоятельно функции sinc и pulstran
6. Упражнения для самостоятельной работы
При самостоятельном выполнении упражнений, приведенных в данном разделе, могут оказаться полезными следующие рекомендации и порядок работы над задачами:
• После загрузки системы MATLAB открыть приложение Simulink.
• В открывшемся окне Simulink Library Browser мышью выбрать File->New->Model, либо символ нового файла, либо нажать клавиши Ctrl+N. В результате на экране появится изображение рабочей области, в которой необходимо конструировать
структурную схему модели решаемой задачи. Эта рабочая область может быть сохранена как файл с именем, выбираемым пользователем.
• Перенести мышью в рабочую область необходимые решающие элементы, источники сигналов и виртуальные измерительные приборы из библиотеки Simulink в открытом окне Simulink Library Browser.
• Скопировать в необходимом количестве элементы, которые встречаются более одного раза, и разместить их в рабочей области так, чтобы их было удобно соединять друг с другом виртуальными проводниками. Оптимальное размещение элементов является достаточно непростой задачей и зависит от опыта и умения исследователя.
• В случае необходимости можно изменить пространственную ориентацию блоков. Для этого необходимо разместить курсор мыши над изображением блока, выделить его однократным нажатием левой клавиши мыши и выбрать мышью команду Format->Rotate Block, либо одновременным нажатием клавиш Ctrl+R. Одна команда поворачивает блок на 90 градусов.
• Соединить блоки между собой в соответствии со структурной схемой решаемой задачи (сформировать структурную схему модели) с помощью мыши.
• Установить необходимые параметры решающих элементов и других блоков, входящих в структурную схему модели с помощью окна параметров блока, вызов которого производится путем двукратного нажатия на левую кнопку мыши, когда курсор находится в пределах изображения блока.
• В окне Simulation строки меню рабочей области выбрать команду Start. Запуск процесса моделирования можно также осуществить одновременным нажатием клавиш CTRL+T.
• Следует помнить, что виртуальные решающие блоки и элементы системы Simulink обладают и другими возможностями, использовать которые можно с помощью электронной системы Help или других учебных пособий по системе MATLAB / Simulink.
6.1. Сформировать и визуализировать сигналы заданной формы.
Указание. Использовать блоки: Constant, Integrator, Gain, Trigonometric Function, Math Function, Sum, Scope,.
Упражнение 2
Указание. Использовать те же блоки, что и в упр. 1, перестроив блок Math Function.
Указание. Использовать блоки: Constant, Integrator, Gain, Trigonometric Function, Math Function, Product, Scope.
Упражнение 4
Указание. Использовать в необходимых количествах блоки: Constant, Integrator, Gain, Math Function, Sum, Scope.
Указание. Использовать блоки: Constant, Integrator, Gain, Math
Function, Sum, MinMax, Scope.
Упражнение 6
Указание. Использовать блоки: Constant, Integrator, Gain, Abs, Math Function, Scope.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
ЛР3 > Сигналы и их свойства. Генерация сигналов в среде MatLab
Руководство по лабораторной работе
Для выполнения лабораторной работы Вам необходимо повторить соответствующие лекции.
Скачать Материалы к лабораторной работе №3.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Гармонические сигналы и их комбинации в среде MatLab создаются с помощью функций Sin(x) и Cos(x). Следующий пример демонстрирует сигнал, представляющий собой сумму двух синусоид – 3Гц с амплитудой 1 В и 40 Гц с амплитудой 0,25 В. Сигнал сформирован для интервала времени от 0 до 1 с, частота дискретизации – 100 Гц.
Пример № 1.
fs = 100; %частота дискретизации 100 Гц
t = 0:1/fs:1; %интервал времени от 0 до 1 сек
Результат работы программы представлен на рисунке 1.
Рисунок 1. Результат работы программы из примера № 1.
Пример № 2.
Fs = 8e3; %частота дискретизации 8 КГц
t = 0:1/Fs:1; %1 секунда дискретных моментов времени
t = t’; %преобразование строки в столбец
A = 2; %амплитуда – 2 В
f0 = 1e3; %частота – 1 КГц
phi = pi/4; %начальная фаза – 45 град
s1 = A*cos(2*pi*f0*t+phi); %гармонический сигнал
alpha = 1e3; %скорость затухания экспоненты
s2 = exp(-alpha*t).*s1; %затухающая синусоида
Результат работы программы представлен на рисунке 2.
Рисунок № 2. Результат работы программы из примера № 2.
Для генерации одиночных импульсов в среде MatLab имеются встроенные функции:
rectpuls – прямоугольный импульс;
tripuls – треугольный импульс;
sinc – импульс вида sin(πt)/ (πt);
gausplus – радиоимпульс с гауссовой огибающей;
pulstran – последовательность из конечного числа импульсов произвольной формы.
Рассмотрим несколько примеров с использованием данных функций.
Функция rectpuls формирует одиночный прямоугольный импульс с единичной амплитудой. Формат вызова данной функции следующий:
y = rectpuls (t, width), где
t – вектор значений времени, width – ширина (длительность) импульса.
В качестве следующего примера рассмотрим генерацию одиночного отрицательного импульса, длительностью 20 мс и амплитудой – минус 5 В (пример № 3):
Пример № 3.
В качестве следующего примера рассмотрим генерацию одиночного треугольного импульса, длительностью 60 мс, амплитудой 10 В и смещением вершины на 15 мс (пример № 4).
Пример № 4
Fs = 1e3; %частота дискретизации
T1 = 0.5; %смещение вершины
T2 = 60e-3; %нижнее основание
s = A*tripuls(t,T2,T1);% генерация импульса
Функция gausplus формирует одиночный радиоимпульс с гауссовой огибающей и единичной амплитудой. Формат вызова данной функции следующий:
y = gauspuls(t, fc, bw, bwr), где
t – вектор значений времени, fc – несущая частота в Гц, bw – относительная ширина спектра (ширина спектра, деленная на несущую частоту), bwr – уровень (в децибелах), по которому производится измерение ширины спектра.
В качестве примера рассмотрим генерацию одиночного радиоимпульса с несущей частотой = 4 КГц, шириной спектра = 400 Гц, амплитудой = 1 В, уровнем измерения ширины спектра = – 20 дБ (пример № 5).
Пример № 5.
Fs = 16e3;% частота дискретизации 16 КГц
Fc = 4e3;%несущая частота 4 КГц
bw = 0.1;%относительная ширина спектра 0.1
s=gauspuls(t,Fc,bw,bwr);% генерация радиоимпульса
Функция pulstran служит для генерации конечной последовательности импульсов одинаковой формы с произвольно задаваемыми задержками и уровнями. Формат вызова этой функции следующий:
y = pulstran(t, d, ‘func’, p1, p2, …), где
t – вектор значений времени, d – вектор задержек, ‘func’ – имя функции, генерирующей одиночный импульс (могут использоваться функции rectpuls,
tripuls, gausplus или собственные функции). Оставшиеся параметры p1, p2, … – дополнительные, они передаются функции ‘func’ при ее вызове.
ЗАДАНИЕ
Исследуйте самостоятельно функции sinc и pulstran
Моделирования в пакете Matlab Simulink
Цель работы:Разработка аналитических моделей для определения поведения
динамических систем, описываемых обыкновенными
дифференциальными уравнениями n-го порядка с постоянными
коэффициентами, реализация этих моделей с помощью пакета Simulink.
Лабораторные работы
Лабораторная работа 3.1.1. Моделирование входных сигналов динамических
Систем
Задание.
Сформировать и визуализировать сигналы заданной формы (см. табл.3.1).
Порядок выполнения работы
Отчет должен содержать:
— исходные данные для моделирования;
| Вариант | Форма сигнала  |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
| | |
 | |
 |
Лабораторная работа 3.1.2. Моделирование временного отклика
Динамических систем
Цель работы.Приобретение практических навыков, необходимых при исследовании
переходных процессов, вызванных ступенчатым воздействием
в динамических системах.
Задание.
Модель динамической системы описывается дифференциальным уравнением
. (3.1)
Порядок выполнения работы
Отчет должен содержать:
— исходные данные для моделирования;
Варианты параметров модели
| Вариант |  |  |  |  |
| 2,3 | ||||
| 1,5 | ||||
| 2,5 | ||||
| 1,5 | ||||
| 2,8 | ||||
| 3,6 | ||||
| 1,8 | ||||
| 2,4 | ||||
| 3,6 | ||||
| 1,6 | ||||
| 3,1 | ||||
| 2,2 | ||||
| 1,7 | ||||
| 2,3 | ||||
| 3,3 | ||||
| 4,1 | ||||
| 1,8 | ||||
| 2,4 | ||||
| 3,3 | ||||
| 2,7 |
Отчет должен содержать:
— исходные данные для моделирования;
— графики переходной и весовой функции.
Лабораторная работа 3.1.3. Моделирование частотного отклика
Динамических систем
Цель работы.Изучение частотных характеристик типовых динамических звеньев
первого и второго порядка.
Задание.
Передаточная функция колебательного звена 2 порядка описывается уравнением
.
а) Построить в Simulink модель для исследования колебательного звена с заданными параметрами 
. Исходные данные для моделирования приведены в табл.3.3.
б) Исследовать влияние заданного параметра (k, T или 
) на вид частотных характеристик (bode, диаграмме Найквиста), рассмотреть следующие значения параметра: 10% от исходного, 50% от исходного, 100% от исходного.
Отчет должен содержать:
— исходные данные для моделирования;
| Вариант | k | T | | Варьировать |
| 0,2 | 0,1 | | ||
| 0,1 | 0,2 | k | ||
| 0,3 | 0,1 | T | ||
| 0,1 | 0,3 | T | ||
| 0,2 | 0,4 | k | ||
| 0,4 | 0,8 | | ||
| 0,5 | 1,3 | k | ||
| 0,1 | | |||
| 0,2 | 0,9 | T | ||
| 0,3 | 0,5 | k | ||
| 0,4 | 0,6 | T | ||
| 0,5 | 0,7 | | ||
| 0,5 | 1,2 | | ||
| 0,4 | 0,5 | T | ||
| 0,3 | 0,6 | k | ||
| 0,2 | 1,1 | | ||
| 0,1 | 1,3 | k | ||
| 0,2 | 0,9 | T | ||
| 0,3 | 0,2 | T | ||
| 0,4 | 0,5 | | ||
| 0,3 | 0,4 | | ||
| 0,6 | 0,1 | T | ||
| 0,2 | 0,3 | k | ||
| 0,4 | 0,2 | T | ||
| 0,4 | 0,5 | |
Лабораторная работа 3.1.4. Анализ динамических свойств на основе
Дифференциальной модели
Задание.
В соответствии с вариантом задания определить реакцию динамической системы, описываемой дифференциальным уравнением (таб. 3.2) при внешнем воздействии заданном в таб.3.1.
Отчет должен содержать:
— исходные данные для моделирования;
— графикиЛАЧХ и ЛФЧХ.
Примеры выполнения лабораторных работ
При структурном моделировании в пакете Simulink необходимо составить схему моделирования. На ней изображаются блоки (усилители, сумматоры, интеграторы и т.д.) и связи между ними. При проведении моделирования эта схема набирается на экране дисплея с помощью мыши или клавиатуры. По своему смыслу этот процесс аналогичен вводу программы, однако он более прост и нагляден. Подробная информация о реализации таких схем в Simulink имеется в разделе 3.3.
Пример 1. Моделирование входных сигналов динамических систем
Постановка задачи.
Построить модель сигнала вида
на интервале [0; 2] и отобразить его на виртуальном осциллографе.
Решение.
Структурная схема моделирования сигнала приведена на рис.3.1.
Сигнал 
задан в параметрах блока Sine Wave (библиотека Sources).
Для сигнала 
используются два блока – блок линейного сигнала Ramp (библиотека Sources) и блок математических функций Fcn (библиотека User-Defined Functions), где была выбрана функция возведения в квадрат. Суммирование составляющих сигнала производится с помощью функции Sum (библиотека Commonly Used Blocks).
Результаты работы выведены на экран осциллографа Skope (библиотека Sinks).
Рис.3.1. Схема моделирования сигнала
Рис.3.2. Параметры блока Sine Wave
Рис.3.3. Сигнал на экране виртуального осциллографа