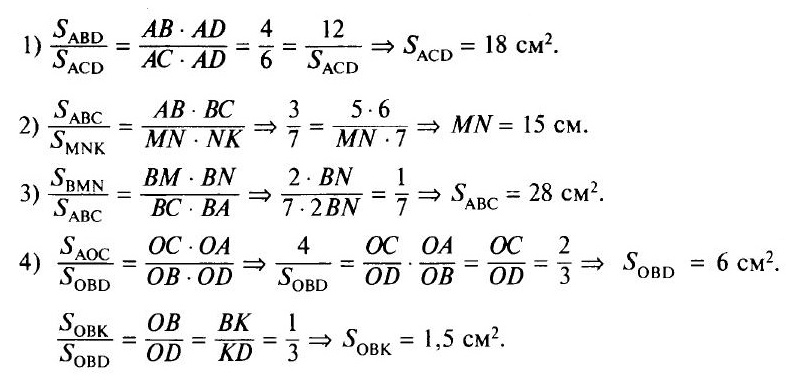сформулировать теорему об отношении площадей подобных треугольников

Геометрия. 8 класс

Отношением отрезков AB и CD называется отношение их длин. Отрезки AB и CD пропорциональны отрезкам A₁B₁ и C₁D₁, если их отношения равны.
AB/(A₁B₁) = CD/(C₁D₁)
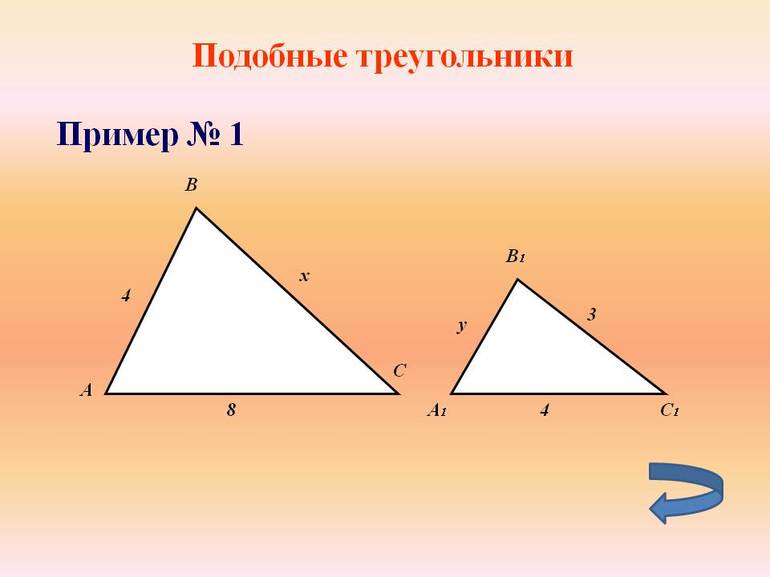
Выясним, пропорциональны ли отрезки на рисунке.

Составим отношения отрезков, учитывая их длины:
AB/AC = 4/12 = 1/3,
AD/DE = 3/9 = 1/3,
DB/BE = 1/5,
Получим, что отрезки AB и AC пропорциональны отрезкам AD и DE. А отрезки AB и AC не пропорциональны отрезкам DB и BE.
Интересное и важное свойство биссектрисы угла треугольника связано с пропорциональностью отрезков.
Пусть дан треугольник АВС, в нем проведена биссектриса АD, докажем, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Дано: ∆ ABC, AD – биссектриса
Доказать: BD/AB = DC/AC
Для доказательства воспользуемся следствиями из формулы площади треугольника:
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

У треугольников ADC и ABD общая высота AH, поэтому
S_ABD/S_ADC = BD/DC
2) У треугольников ADC и ABD
∠CAD = ∠BAD, поэтому
S_ABD/S_ADC = (AB ∙ AD)/(AC ∙ AD) = AB/AC
3) BD/DC = AB/AC
Или
BD/AB = DC/AC
В геометрии фигуры одинаковой формы называют подобными.
Рассмотрим два треугольника, углы которых равны.
∆ ABC и ∆A₁B₁C₁
∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁
Тогда стороны AB и A₁B₁, BC и B₁C₁, CA и C₁A₁ называются сходственными.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
∆ ABC

Источник

Сформулировать теорему об отношении площадей подобных треугольников

Поурочное планирование по геометрии для 8 класса. Ориентировано на работу с УМК Атанасян и др. Геометрия 8 класс. Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников. Вернуться к Списку уроков Тематического планирования.

Урок 32. Отношение площадей
подобных треугольников

Основные дидактические цели урока: закрепить понятия пропорциональных отрезков и подобных треугольников; совершенствовать навыки решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; рассмотреть теорему об отношении площадей подобных треугольников и показать ее применение в процессе решения задач.

Ход урока

I. Организационный момент

(Учитель сообщает тему урока, формулирует цели урока.)

II. Актуализация знаний учащихся. Мотивация к учебной деятельности

1. Теоретический опрос.

(Один ученик оформляет доказательство теоремы на доске.)
1) Ответить на вопросы 1—3 учебника.
2) Доказать свойство биссектрисы треугольника.

2. Проверка домашнего задания.

(Учитель проверяет решение задач № 538, 542. Два ученика готовят решение на доске.)

Задача № 538

Задача № 542

3. Работа по индивидуальным карточкам.

(3—6 учеников работают по карточкам.)

I уровень сложности

II уровень сложности

III уровень сложности

Ответы и указания к задачам по готовым чертежам:

(После окончания самостоятельного решения задач и самопроверки по готовым ответам выполняется самооценка.) Критерии оценивания:

III. Работа по теме урока

(Учитель делит класс на группы для решения задания творческого характера. После завершения работы заслушиваются и обсуждаются варианты решений.)

Задание. Треугольники АВС и А1В1С1 подобны с коэффициентом подобия k. Найти отношение их площадей.

Вывод. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

IV. Закрепление изученного материала

Задача № 545

Вопросы для обсуждения.

V. Самостоятельная работа

I уровень сложности

II уровень сложности

III уровень сложности

VI. Рефлексия учебной деятельности

Домашнее задание

I уровень сложности: В подобных треугольниках АВС и KMN равны углы В и М, С и N, АС = 3 см, KN = 6 см, MN = 4 см, ∠AX = 30°. Найдите ВС, ∠K; отношение площадей треугольников AВС и KMN; АЕ и BE, если известно, что СЕ — биссектриса треугольника АВС, АВ = 3,5 см.

II уровень сложности: В прямоугольном треугольнике ABC ∠C = 90°, ∠B = 30°, АВ = 12 см, CD — высота. Докажите, что ΔACD подобен ΔАВС, найдите отношение их площадей и отрезки, на которые биссектриса угла А делит катет ВС.

Вы смотрели: Поурочное планирование по геометрии для 8 класса. УМК Атанасян и др. (Просвещение). Глава VII. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ. Урок 32. Отношение площадей подобных треугольников.

Источник

Сформулировать теорему об отношении площадей подобных треугольников

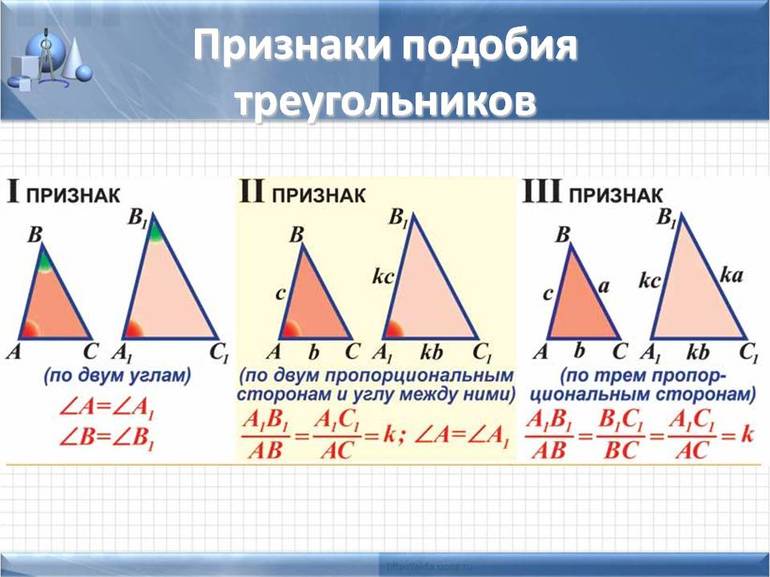
Два треугольника подобны:

Из признаков подобия следует утверждения, которые удобно использовать в решении задач:

1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

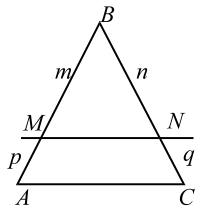Рис. 5

3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.\;\left.\beginBC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm<по>\;\mathrm<двум>\;\mathrm<углам>)\end\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)

$$2.\;\left.\beginMO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end\right|\Rightarrow\dfrac xa=\dfrac p$$. (2)

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.

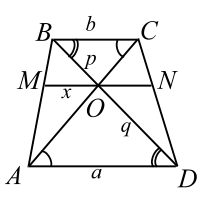Рис. 6

Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.

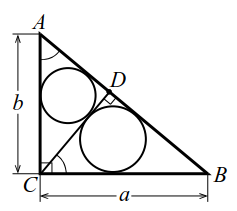Рис. 7

Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.

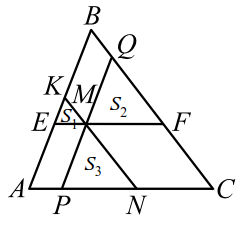Рис. 8

Свойства медиан, высот, биссектрис треугольника

В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.

Рис. 9

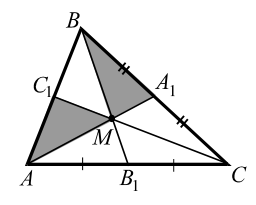
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

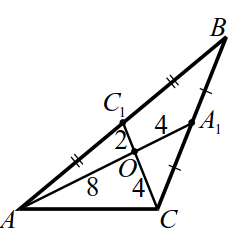Рис. 10

2. Площадь треугольника находим по формуле Герона:

Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Были доказаны также две леммы о высотах

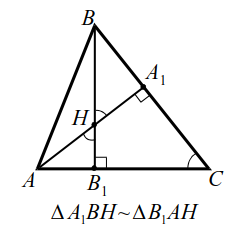
1-ая лемма.

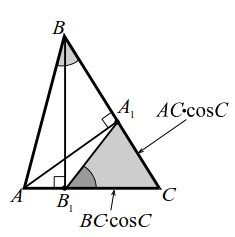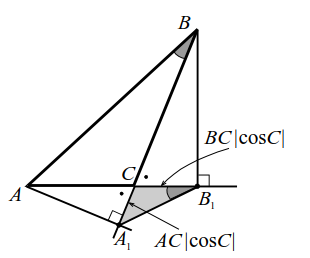Рис. 11a	Рис. 11б

2-ая лемма.

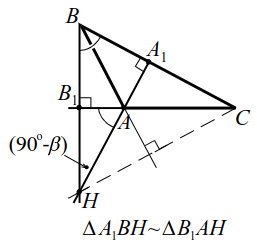Рис. 12a	Рис. 12б

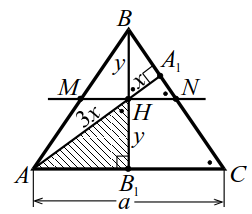Рис. 13

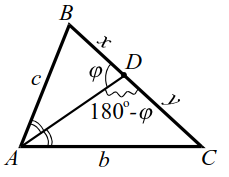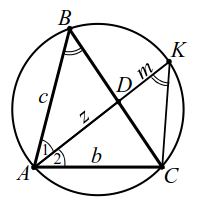Рис. 14	Рис. 14а

Источник

Общие сведения

Специалисты рекомендуют начинать любое обучение с азов. Следует применять принцип, который называется «от простого к сложному». В плоскостной геометрии (Евклида) существует два понятия: аксиомы и теоремы. К первым относятся утверждения, не требующие доказательства. Они являются базовыми элементами науки и позволяют доказывать другие гипотезы или утверждения.

Кроме того, на основании доказанных гипотез можно производить операции по доказательству более сложных теорем. Иными словами, геометрия состоит из базисных элементов — аксиом, при использовании которых можно преобразовывать утверждения в неоспоримые факты, а также при комбинациях появляется возможность доказательства более сложных (составных) элементов. Примером последнего случая является гипотеза Пифагора для прямоугольного треугольника. Чтобы ее доказать, нужно знать аксиомы геометрии, а также теорему об отношении площадей подобных треугольников (S/S’). Далее необходимо разобрать основные объекты геометрии.

Объекты геометрии

Простейшим объектом геометрии является точка. С помощью нее строятся простые фигуры, благодаря которым образуются более сложные формы. К элементарным компонентам можно отнести следующие: прямая, отрезок, луч. Первая состоит из множества точек, соединенных между собой в одной плоскости и находящихся в поперечном сечении, диаметр которого эквивалентен диаметру точек. При соединении простейших объектов получается бесконечная линия без перегибов.

Лучом называется часть прямой, имеющая начальную точку, но у которой нет конечной границы. Еще существует один элемент, у которого присутствуют обе границы (левая и правая). Он называется отрезком. Следует отметить, что луч и отрезок могут лежать на одной прямой, а также последний может являться частью первого.

При комбинации двух лучей, исходящих из одной точки получается плоский угол. Он измеряется в градусах или радианах. Следует отметить, что в геометрии существует понятие «нулевого» угла. Это возможно, когда лучи совпадают. При комбинации трех углов можно получить треугольник. Существует также другое определение этой фигуры: треугольником (Δ) называется фигура, состоящая из трех точек, одна из которых не лежит на одной прямой с остальными.

Треугольники бывают разносторонними, равнобедренными и равносторонними. Кроме того, в зависимости от градусной меры, они делятся на такие классы: остроугольные, тупоугольные и прямоугольные. Необходимо также отметить, что сумма углов этой геометрической фигуры эквивалентна 180 градусам.

Нужно обратить внимание на такие термины: высоту, медиану и биссектрису. Первой называется перпендикуляр, проведенный из вершины к противоположной стороне. Медиана — отрезок, проведенный из противоположной вершины к середине стороны. Биссектрисой угла является луч или отрезок, который делит его на два равнозначных по величине. В равнобедренном и равностороннем Δ эти элементы совпадают.

Основные аксиомы Евклида

Аксиомой называется утверждение, не требующее доказательств и воспринимаемое в виде факта. Существуют следующие утверждения, которые можно применять при решении задач:

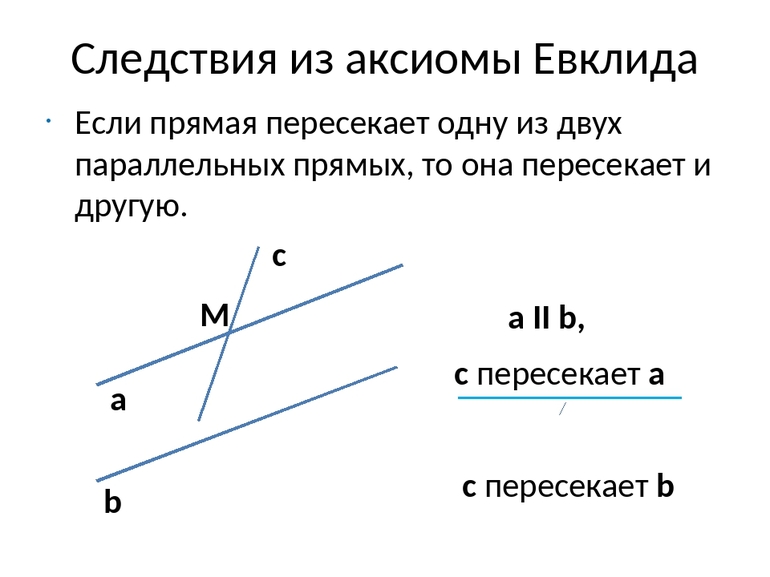
Следует обратить внимание на последнюю аксиому. Она позволяет строить любые фигуры на плоскости и в пространстве. Математики очень часто применяют такой прием при решении задач и доказательстве некоторых тождеств при помощи создания дополнительных элементов на чертеже.

Например, в некотором упражнении по нахождению отдельных параметров треугольника в условии содержится очень мало данных. Последний можно вписать в окружность или дополнить до квадрата или прямоугольника. Далее следует разобраться в признаках подобия треугольников.

Подобие двух треугольников

Треугольники являются подобными, когда углы одного эквивалентны всем градусным мерам углов другого, а стороны одного равны сторонам другого, с учетом коэффициента гомотетии. Последний называют еще коэффициентом подобия. Он равен отношению сторон подобных треугольников. Например, дано два подобных Δ ABC и A’B’C’ (больший). Коэффициент подобия треугольников обозначается литерой «k». Он больше 0 и вычисляется по такой формуле: k = A’B’ / AB = B’C’ / BC = A’C’ / AC. Подобие фигур обозначается таким образом: ΔABC ∼ ΔA’B’C’.

Не во всех случаях бывают известны углы и стороны фигур. Для этого были сформулированы три признака (условия или критерия), по которым можно определить подобие.

Первое условие

Формулировка первого признака подобия треугольников гласит, что равенство двух углов между собой соответствует подобию двух фигур. Подробнее исходные данные записываются в таком виде: ΔABC ∼ ΔA’B’C’, когда ∠ВАС = ∠B’A’C’ и ∠ABC = ∠A’B’C’. Доказать утверждение довольно просто. Для этого следует рассчитать третий угол у треугольников исходя из того, что сумма трех углов составляет 180 градусов.

Далее необходимо наложить один Δ на другой, чтобы ∠ВАС совпал с ∠B’A’C’. Используя теорему Фалеса для сторон угла, которые делят на отрезки AC / A’C’ = BC / B’C’ вершины малого Δ на пропорциональные части. Аналогично доказывается пропорциональность для двух других сторон. Однако для этого следует наложить уже треугольники таким образом, чтобы совпали другие углы. Такие же действия проделать и для третьего угла. На основании определения о подобии треугольников утверждение доказано. Из доказательства математики получили некоторые следствия, которые будут очень полезны при решении задач:

Равенство AC / A’C’ = BC / B’C’ эквивалентно коэффициенту подобия. Этот факт можно использовать при решении задач и доказательства других геометрических утверждений или тождеств.

Второй критерий

Математики выделяют еще один признак подобия треугольников по двум пропорциональным сторонам и углу между ними. Для доказательства следует рассмотреть ΔABC и ΔA’B’C’ со сторонами, связанными таким тождеством: AB / A’B’ = AC / A’C’. Кроме того, углы между ними равны: ∠ВАС = ∠B’A’C’. Далее нужно достроить ΔABC до четырехугольника ABCС». Вершина С» должна располагаться в зеркальном отображении относительно стороны AB. Полученный ΔABC» ∼ ΔA’B’C’ по I признаку, поскольку у них два угла равны. Следовательно, тождество можно править таким образом: AB / A’B’ = AC» / A’C’.

По условию должно выполняться условие AB / A’B’ = AC / A’C’. Тогда AC = AC». На основании этого факта можно сделать вывод о равенстве ΔABC и ΔABC». Следовательно, теорема доказана, поскольку эти треугольники (ΔABC» и ΔA’B’C’) подобны по I признаку.

Третий признак

Третий признак подобия двух треугольников формулируется таким образом: два треугольника являются подобными, когда стороны одного пропорциональны сторонам другой фигуры. Для доказательства необходимо рассмотреть ΔABC и ΔA’B’C’ со сторонами: AB / A’B’ = AC / A’C’ = BC / B’C’.

Математики рекомендуют отметить некоторую точку C» относительно стороны AB. Она не должна лежать на последней. Кроме того, расстояния от C и C» до стороны AB должны быть эквивалентны. Иными словами, следует построить ΔABС», который является «зеркальным» отображением ΔABC относительно его стороны AB. Если AB / A’B’ = AC» / A’C’, то ΔABC» ∼ ΔA’B’C’ по I признаку.

Следующий шаг — доказательство равенства ΔABC и ΔABC». Они равны по двум сторонам AC = AC» и BC = BC». Следовательно, ΔABC ∼ ΔA’B’C’ подобные.

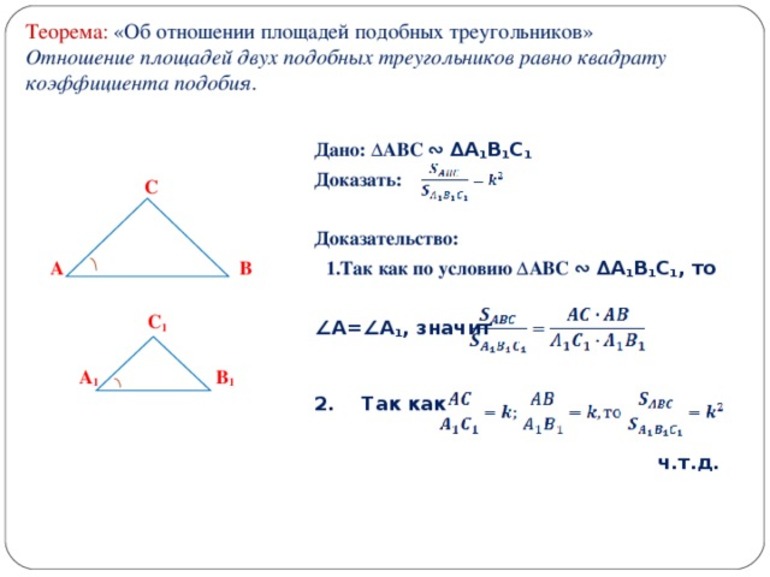
Теорема об отношении площадей

Для решения задач специалисты рекомендуют применять еще теорему об отношении площадей. Обязательным условием ее использования являются ΔABC ∼ ΔA’B’C’ с коэффициентом подобия «k». Ее формулировка имеет такой вид: величина отношения площадей двух подобных треугольников прямо пропорциональна квадрату гомотетии.

Некоторые свойства и следствия

Математики также считают, что используя некоторые свойства и следствия из теорем, можно расширить возможности по решению задач. Свойства подобных треугольников можно применять и к другим плоским или объемным фигурам. Следствия классифицируются на несколько типов:

Пример решения

Существуют множество типов задач, однако наиболее часто попадаются такие, в которых необходимо доказать, что фигуры являются подобными. Стороны ΔABC равны таким значениям: 10, 12 и 25. Кроме того, существует еще ΔA’B’C’ со сторонами 5, 6 и 10. Фигуры не имеют точек пересечения. Необходимо доказать их подобие.

Для решения рисунок чертить необязательно, поскольку для доказательства необходимо применение не геометрического метода, а алгебраического. Следует ввести обозначения для ΔABC: AB = 10, BC = 12 и AC = 25. Аналогичную процедуру необходимо сделать для ΔA’B’C’: сторона A’B’ равна числу 5, B’C’ = 6 и A’C’ = 10.

Далее нужно вычислить коэффициент k для каждой из сторон: k1 = AB / A’B’ = 10 / 5 = 2, k2 = BC / B’C’ = 12 / 6 = 2 и k3 = AC / A’C’ = 25 / 10 = 2,5. Из соотношений следует, что фигуры не являются подобными, поскольку не выполняется такое равенство: k = k1 = k2 = k3. Для наглядности можно построить также таблицу со значениями коэффициентов.

Таким образом, для решения задач по нахождению параметров подобных треугольников необходимо знать признаки подобия, а также некоторые свойства, которые рекомендуют использовать специалисты-математики.

Источник

Подобные треугольники. Отношение периметров подобных треугольников. Коэффициент подобия

Что такое подобные треугольники?

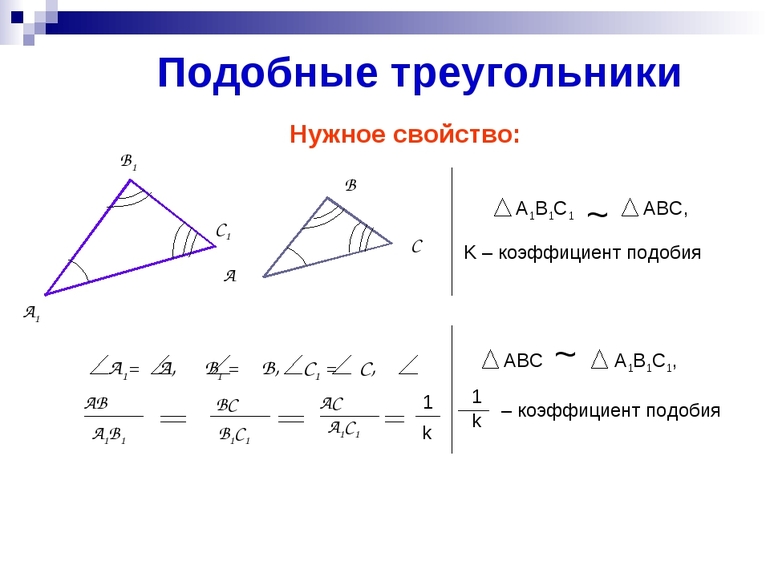
Подобные треугольники определение

Подобные треугольники определение:

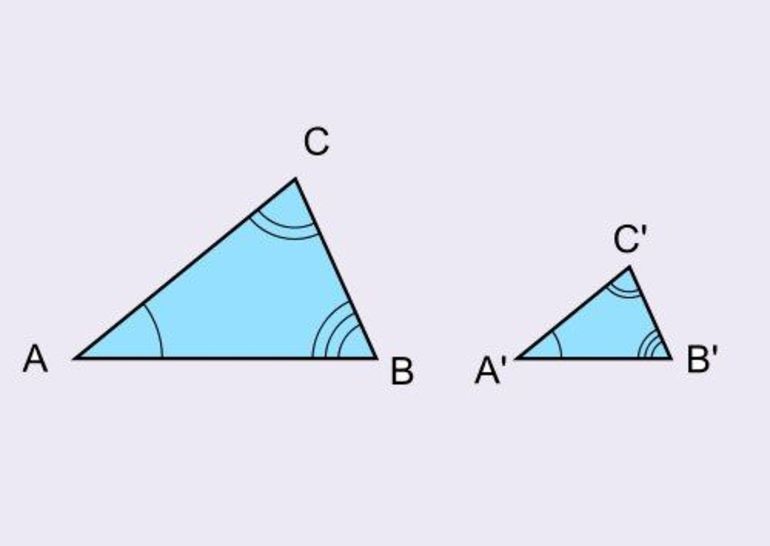
На рисунке изображены два подобных треугольника, у них углы соответственно равны, т.е. угол A равен углу A₁, угол B равен углу B₁, угол C равен углу C₁.

Сходственные стороны треугольников

Сходственные стороны треугольников пропорциональны:

здесь k называется коэффициентом подобия.

Отношение площадей подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия:

Отношение периметров подобных треугольников

Отношение периметров подобных треугольников:

Докажем это утверждение. Пусть имеются два подобных треугольника ABC и A₁B₁C₁. По определению подобных треугольников их сходственные стороны пропорциональны:

Периметр треугольника ABC равен сумме длин его трёх сторон:

Сумма в скобках в правой части равенства представляет собой периметр треугольника A₁B₁C₁. Разделим обе части равенства на периметр A₁B₁ + B₁C₁ + A₁C₁. Получаем:

что и требовалось доказать. Итак, отношение периметров подобных треугольников равно коэффициенту подобия.

Для установления факта подобия двух треугольников используют признаки подобия треугольников:

Источник