суждения типа а и о е и i находятся в отношении
Логический квадрат (отношения между суждениями)



Сравнимые (идентичные по материалу) суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику являются сравнимыми, так как у них совпадают субъекты и предикаты, а кванторы и связки различаются.
Несравнимые суждения имеют разные субъекты и предикаты. Например, суждения: Все школьники изучают математику, Некоторые спортсмены – это олимпийские чемпионы являются несравнимыми, так как субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыми называются суждения, которые могут быть одновременно истинными. Например, суждения Некоторые люди – это спортсмены, Некоторые люди – это не спортсмены являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения Все школьники изучают математику, Некоторые школьники не изучают математику не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в отношениях равнозначности, подчинения или частичного совпадения.
Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения Москва является древним городом, Столица России является древним городом находятся в отношении равнозначности.
Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения Все растения являются живыми организмами, Все цветы (некоторые растения ) являются живыми организмами находятся в отношении подчинения.
Несовместимые суждения могут находиться в отношениях противоположности или противоречия.
Противоположность – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения Все люди являются правдивыми и Все люди не являются правдивыми находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные (Д) и общеотрицательные (Е ).
Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Вернемся к приведенным выше суждениям и убедимся в этом: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми. Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант.
Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями Все люди являются правдивыми и Все люди не являются правдивыми есть третий, средний вариант Некоторые люди являются правдивыми, а некоторые не являются таковыми, который, будучи истинным суждением, обусловливает одновременную ложность двух крайних противоположных суждений.
Противоречие – это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объемами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения Все люди являются правдивыми и Некоторые люди не являются правдивыми находятся в отношении противоречия.
Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот, ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы еще вернемся, когда речь пойдет о логических законах противоречия и исключенного третьего.
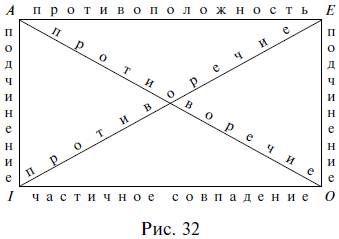
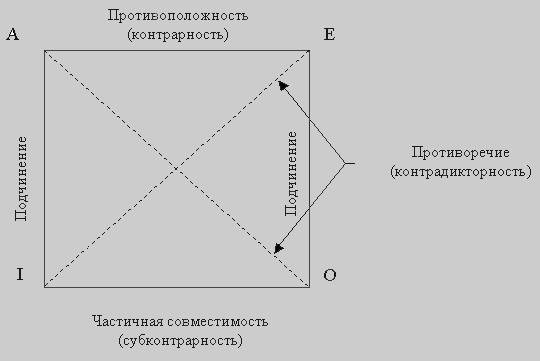
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан еще средневековыми логиками.
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия.
Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О.
Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения Все люди изучали логику и Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А ), а второе частноотрицательным (О ), мы без труда устанавливаем отношение между ними с помощью логического квадрата – это противоречие.
Суждения Все люди изучали логику (А ) и Некоторые люди изучали логику (I ) находятся в отношении подчинения, а суждения Все люди изучали логику (А ) и Все люди не изучали логику (Е ) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений (в отличие от понятий) является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так, если суждение вида А является истинным или ложным, то три других (I, Е, О ), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида А ) тоже являются истинными или ложными.
Например, если суждение вида А: Все тигры – это хищники – истинно, то суждение вида I. Некоторые тигры – это хищники – также истинно (если все тигры – хищники, то и часть из них, т. е. некоторые тигры, – это тоже хищники); суждение вида Е Все тигры – это не хищники – ложно, и суждение вида О: Некоторые тигры – это не хищники – также является ложным. Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
9. Краткий курс классической логики. Суждение
Суждение – это форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: «Некоторые студенты – отличники», «Все люди – смертные».
Суждения составляется из понятий, оно предоставляет собой чаще всего повествовательное предложение. В редких случаях оно бывает риторическое-восклицательное или риторическое-вопросительное предложение, которое что-то утверждает или отрицает.
Бывают простые и сложные суждения, сложные суждения складываются из двух или более простых суждений соединённых союзом.
Суждение на отмену от понятий бывают истинные и ложные, а так же имеют сложную структуру, которая складывается из таких понятий:
Субъект и предикат суждения могут состоять в отношениях:
1.Равнозначности – когда объем субъекта равен объёму предиката. «Все квадраты – равносторонние прямоугольники».
2.Подчинения – когда объем субъекта входит в объем предиката или наоборот. «Все березы – это деревья». Объем понятия деревья больше понятия березы, так как береза только одно из разновидностей деревьев.
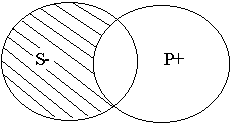
3.Пересечения – когда объемы субъекта и предиката пересекаются частично, к примеру, «Некоторые литераторы – это лауреаты нобелевской премии». Литераторы могут быть лауреатами нобелевской премии, но могут и не быть, так же как и лауреаты нобелевской премии могут быть литераторами, но могут ими и не быть. Объем этих понятий совпадает только в некоторых случаях, потому субъект и предикат находятся в отношении пересечения.
4.Несовместимости – когда объемы субъекта и предиката не имеют общих точек соприкосновения. «Звезды – это не планеты». Чаще субъект и предикат, входя в третье более общее понятия, в нашем случае – это небесные тела.
Важно заметить, что при обращении, суждения меняют свой тип, согласно ниже приведенных примеров:
Суждения типа А:
равнозначности – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа I:
пересечения – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа Е:
несовместимости – обращается в самое себя.
Суждения типа О:
пересечения – обращению не поддается.
подчинения – обращению не поддаётся.
Второе действие над суждениями — превращения. Оно заключается в том, что у суждения меняется связка, положительная на отрицательную или наоборот. При этом предикат суждения меняется на противоречащий, перед ним ставиться частица «не». Вернемся к нашему исходному суждению: «Все акулы – являются рыбами». Результатом превращения будет суждения: «Все акулы не являются не рыбами». Выглядит это суждения непривычно, однако это более короткое изречение той мысли, что если какое-то животное не являются акулой, то оно не являются и рыбой. Или, что если какое-то животное является акулой то оно обязательно должно являться рыбой, ни одна акула не может быть таким существом, которое бы не являлось при этом рыбой.
В отличие от обращения превращение не зависит от характера отношения субъекта и предиката простого суждения:
Суждения типа А всегда превращается в суждения типа Е, и наоборот.
Суждения типа I всегда превращается в суждения типа О, и наоборот.
При действии противоставления предикату суждения меняют свой тип, аналогично обращении.
В итоге, из одного суждения, мы можем получить четыре:
1. Исходное суждение: «Все акулы являются рыбами».
2. Результат обращения: «Некоторые рыбы – это акулы».
3. Результат превращения: «Все акулы не являются не рыбами».
4. Результат противоставления предикату: «Все не рыбы не являются акулами».
Если мы разобрались с этим, то совершить превращения и противоставления предикату этого суждения совсем не проблематично. Получиться, как и в первом варианте — четыре суждения:
Исходное суждение: «Идти назад – значит не идти вперед»
Обращения: «Иногда не идти вперед, значит идти назад».
Превращения: «Идти назад не означает, не идти вперед».
Противоставление предикату: «Иногда не идти вперед не означает, не идти назад».
Несовместимые суждения находятся в отношениях:
Противоположности (контарность) – суждения, в которых, так же как при отношении частичного совпадения, субъект и предикат совпадает, а связка отличается, но в этом случае суждения могут быть только общими: общеутвердительными (А) или общеотрицательными (О). «Все люди – лгут», «Все люди – не лгут». Важным признаком противоположных суждений является то, что они не могут быть одновременно истинные как несовместимые, но при этом могут быть одновременно ложными. Между этими суждениями всегда можно вставить третье, нейтральное утверждение. В нашем примере это «Некоторые люди лгут, а некоторые не лгут». Это суждение, будучи истинным, доказывает ложность двух первых.
Противоречия (контрадикторность) – это отношения между двумя суждениями в которых предикаты совпадают, связки отличаются, а субъекты находятся в родовом, видовом отношении, то есть отличаются объемами. «Все люди – являются разумными существами», Некоторые люди – не являются разумными существами». На отмену от противоположных суждений противоречивые, не могу быть одновременно ложными. Ложность одного непременно будет доказательством истинности другого, и наоборот.
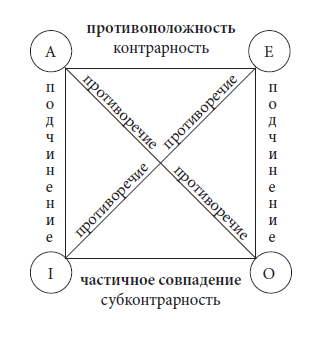
Возможные отношения между простыми суждениями отображают посредством, так называемого логического квадрата:
Истинное значение суждения, связано с истинностью значений всех других сравнимых суждений. К примеру если суждения типа А: «Все акулы – являются рыбами» истинно, смотря на логический квадрат, можно определить, что суждения типа I: «Некоторые рыбы – являются акулами», тоже будет истинным. Суждения типа Е: «Все акулы – не являются рыбами», точно так же как и суждения типа О: «Некоторые акулы – не являются рыбами», будут ложными.
Еще несколько слов о сложных суждениях. В зависимости от союза, которым соединяются простые суждения в сложные, выделяют пять видов сложного суждения:
Логический квадрат
Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками.
Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так суждения вида А и вида I, а также суждения вида Е и вида О находятся в отношении подчинения. Суждения вида А и вида Е находятся в отношении противоположности, а суждения вида I и вида О – частичного совпадения. Суждения вида А и вида О, а также суждения вида Е и вида I находятся в отношении противоречия.
Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т.е. равнозначность – это отношение между суждениями А и А, I и I, Е и Е, О и О. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: Все люди изучали логику и
Некоторые люди не изучали логику. Видя, что первое суждение является общеутвердительным (А), а второе частноотрицательным (О), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Также суждения: Все люди изучали логику (А) и Некоторые люди изучали логику (I) находятся в отношении подчинения, а суждения: Все люди изучали логику (А) и Все люди не изучали логику (Е) находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными. Что касается сравнимых суждений, о которых идет речь в данном параграфе, то истинностные значения каждого из них определенным образом связаны с истинностными значениями остальных. Так если суждение вида А является истинным или ложным, то три других (I, Е, О) сравнимых с ним суждения (т. е. имеющих сходные с ним субъекты и предикаты) в зависимости от этого (т. е. от истинности или ложности суждения вида А) тоже являются истинными или ложными. Например, если суждение вида А: Все тигры – это хищники яляется истинным, то суждение вида I: Некоторые тигры – это хищники также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида Е: Все тигры – это не хищники является лож-ным, и суждение вида О: Некоторые тигры – это не хищники также является ложным.
Таким образом, в данном случае из истинности суждения вида А вытекает истинность суждения вида I и ложность суждений вида Е и вида О (разумеется, речь идет о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
Далее представлены все случаи отношений между истинностными значениями простых сравнимых суждений.
Используя рассмотренные правила, можно делать выводы об истинности простых сравнимых суждений с помощью логического квадрата (или, как часто говорят в логике, – по логическому квадрату). Выше был приведен пример таких выводов на основе суждения вида А: Все тигры являются хищниками, где из его истинности вытекали определенные истинностные значения других суждений – I, Е, О. Рассмотрим еще один при- мер.
Возьмем суждение вида Е: Все треугольники не являются квадратами и сделаем из его истинности выводы об истинностных значениях суждений А, I, О. Когда данное суждение вида Е истинно (см. правила выше), то суждение вида А: Все треугольники являются квадратами ложно, суждение вида I: Некоторые треугольники являются квадратами также лож- но, а суждение вида О: Некоторые треугольники не являются квадратами истинно (если все треугольники не являются квадратами, то и часть треугольников, т. е. некоторые треугольники также не являются ими).
Логические отношения между суждениями (логический квадрат)
Основу отношений между суждениями составляет их сходство по смыслу и логическим значениям (истинности и ложности). В силу этого отношения устанавливаются не между любыми, а лишь между сравнимыми, т.е. имеющими общий смысл, суждениями.
Несравнимыми среди простых являются суждения, имеющие:
Таковы, например, два суждения:
«Среди космонавтов есть летчики »; «Среди космонавтов есть женщины ».
Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором (суждения одинаковой материи):
Среди сравнимых различают совместимые и несовместимые суждения.
Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемой логическим квадратом.
Логический квадрат
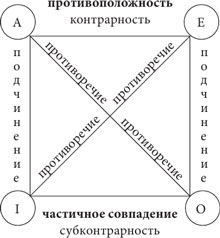
Отношение совместимости
Виды совместимости:
Эквивалентные суждения имеют одинаковые логические характеристики:
С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются.
Различия между высказываниями, содержащими простые эквивалентные суждения, проявляются главным образом словесно.
Например, различными словами могут быть выражены кванторы: «некоторые», «иногда», «как правило» и т.п.; использованы синонимы для выражения субъекта или предиката; суждения могут быть сформулированы на различных национальных языках: «Это стол», «It is a table».
Эту особенность эквивалентных суждений надо учитывать при анализе правовых контекстов, при переводах с одного языка на другой, при сравнении словесно различных утверждений в процессе дискуссии.
Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
При ложности одного из них другое будет истинным. Например, при ложности суждения «Некоторые злаки ядовиты» будет истинным суждение «Некоторые злаки не являются ядовитыми».
В то же время при истинности одного из частных суждений другое может быть как истинным, так и ложным.
Подчинение имеет место между суждениями А и I, E и О. Для них характерны следующие две зависимости:
Например, при истинности общего суждения «Всякое правоотношение регулируется нормами права» истинным будет и частное — «Некоторые правоотношения регулируются нормами права».
При истинности суждения «Ни один кооператив не относится к государственным организациям» будет истинным и суждение «Некоторые кооперативы не относятся к государственным организациям».
Например, если неверно утверждение, что «Некоторые хищения совершаются по неосторожности», то тем более будет неверным утверждение «Всякое хищение совершается по неосторожности».
При подчинении остаются неопределенными следующие зависимости:
Отношение несовместимости
Несовместимыми являются суждения
которые одновременно не могут быть истинными.
Виды несовместимости:
Противоположными (контрарными) являются суждения А и Е, которые одновременно
Истинность одного из противоположных суждений определяет ложность другого. Например, истинность суждения «Все офицеры — военнослужащие» определяет ложность суждения «Ни один офицер не является военнослужащим».
При ложности же одного из противоположных суждений другое остается неопределенным — оно может быть как истинным, так и ложным. Так, например, при ложности суждения «Все птицы улетают зимой в теплые края» ему противоположное «Ни одна птица не улетает зимой в теплые края» тоже оказывается ложным. В другом случае при ложности суждения «Ни один судья не является юристом» ему противоположное «Все судьи — юристы» будет истинным.
Для противоречия характерна строгая, или альтернативная несовместимость:
Отношения между такими суждениями регулируются законом исключенного третьего.
Например, если признается истинным суждение «Все принципиальные люди признают свои ошибки», то ложным будет ему альтернативное: «Некоторые принципиальные люди не признают своих ошибок».
Следует отметить, что несовместимые единичные суждения могут находиться лишь в отношении противоречия и не могут находиться в отношении противоположности, ибо каждому отдельному предмету может быть либо присущ, либо не присущ определенный признак.
Например, суждения «Суд вынес обвинительный приговор по делу Л.» и «Суд не вынес обвинительного приговора по делу Л.» находятся в отношении противоречия: если первое суждение истинно, то признается ложность второго, и наоборот.
Суждения типа а и о е и i находятся в отношении
мЕЛГЙС 4 ртпуфпе ухцдеойе
1. пВЭБС ИБТБЛФЕТЙУФЙЛБ УХЦДЕОЙС.
2. уФТХЛФХТБ Й ЛМБУУЙЖЙЛБГЙС РТПУФПЗП УХЦДЕОЙС
рПМОБС УФТХЛФХТБ РТПУФПЗП УХЦДЕОЙС ЧЛМАЮБЕФ ЮЕФЩТЕ ЬМЕНЕОФБ:
УЧСЪЛБ (Ч СЪЩЛПЧПК ЖПТНЕ ЧЩТБЦБЕФУС УМПЧБНЙ «ЕУФШ/ОЕ ЕУФШ», «УХФШ/ОЕ УХФШ, «СЧМСЕФУС/ОЕ СЧМСЕФУС» Й Ф.Р., МЙВП ЧППВЭЕ ФПМШЛП РПДТБЪХНЕЧБЕФУС). пФТБЦБЕФ ОБМЙЮЙЕ /ПФУХФУФЧЙЕ ПРТЕДЕМЕООПК УЧСЪЙ УХВЯЕЛФБ Й РТЕДЙЛБФБ;
рТПУФЩЕ УХЦДЕОЙС РПДТБЪДЕМСАФУС РП ЛБЮЕУФЧХ ОБ: ХФЧЕТДЙФЕМШОЩЕ Й ПФТЙГБФЕМШОЩЕ, Б РП ЛПМЙЮЕУФЧХ ОБ:
рП ИБТБЛФЕТХ РТЕДЙЛБФБ ТБЪМЙЮБАФ УХЦДЕОЙС:
БФТЙВХФЙЧОЩЕ. бФТЙВХФЙЧОЩН ОБЪЩЧБЕФУС УХЦДЕОЙЕ П РТЙЪОБЛЕ РТЕДНЕФБ, ОБРТЙНЕТ: «мЙУФ ЪЕМЕОЩК»;
У ПФОПЫЕОЙЕН. тЕМСФЙЧОЩН ОБЪЩЧБЕФУС УХЦДЕОЙЕ ПВ ПФОПЫЕОЙЙ НЕЦДХ РТЕДНЕФБНЙ. оБРТЙНЕТ, «нПУЛЧБ ВПМШЫЕ лТБУОПСТУЛБ»;
УХЭЕУФЧПЧБОЙС. ч УХЦДЕОЙСИ УХЭЕУФЧПЧБОЙС ЧЩТБЦБЕФУС УБН ЖБЛФ УХЭЕУФЧПЧБОЙС ЙМЙ ОЕУХЭЕУФЧПЧБОЙС РТЕДНЕФБ УХЦДЕОЙС. оБРТЙНЕТ: «чЩУЫЕЕ ПВТБЪПЧБОЙЕ ЕУФШ».
тБУРТЕДЕМЕООПУФШ ФЕТНЙОПЧ Ч УХЦДЕОЙСИ
пВЯЕДЙОСС ЛПМЙЮЕУФЧЕООХА Й ЛБЮЕУФЧЕООХА ИБТБЛФЕТЙУФЙЛЙ, УХЦДЕОЙС ДЕМСФУС ОБ:
фЕТНЙО УЮЙФБЕФУС ТБУРТЕДЕМЕООЩН (ПВПЪОБЮБЕФУС»+»), ЕУМЙ ПО ЧЪСФ Ч РПМОПН ПВЯЕНЕ. фЕТНЙО УЮЙФБЕФУС ОЕТБУРТЕДЕМЕООЩН (ПВПЪОБЮБЕФУС»-«), ЕУМЙ ПО ЧЪСФ Ч ЮБУФЙ ПВЯЕНБ.
уХЦДЕОЙЕ б: пВЭЕХФЧЕТДЙФЕМШОПЕ
«чУЕ УФХДЕОФЩ ОБЫЕК ЗТХРРЩ УДБМЙ ЪБЮЕФ РП МПЗЙЛЕ»
уХЦДЕОЙЕ I: юБУФОПХФЧЕТДЙФЕМШОПЕ
«оЕЛПФПТЩЕ УФХДЕОФЩ УДБМЙ ЪБЮЕФ»
уХЦДЕОЙЕ е: пВЭЕПФТЙГБФЕМШОПЕ
«оЙ ПДЙО УФХДЕОФ ОЕ УДБМ ЪБЮЕФ»
уХЦДЕОЙЕ п: юБУФОППФТЙГБФЕМШОПЕ
«оЕЛПФПТЩЕ УФХДЕОФЩ ОЕ УДБМЙ ЪБЮЕФ»
3. пФОПЫЕОЙС НЕЦДХ РТПУФЩНЙ УХЦДЕОЙСНЙ. мПЗЙЮЕУЛЙК ЛЧБДТБФ.
оЕУТБЧОЙНЩНЙ УТЕДЙ РТПУФЩИ УХЦДЕОЙК СЧМСАФУС УХЦДЕОЙС, ЙНЕАЭЙЕ ТБЪМЙЮОЩЕ УХВЯЕЛФЩ ЙМЙ РТЕДЙЛБФЩ.
уТБЧОЙНЩНЙ СЧМСАФУС УХЦДЕОЙС У ПДЙОБЛПЧЩНЙ УХВЯЕЛФБНЙ Й РТЕДЙЛБФБНЙ.
дМС ЙММАУФТБГЙЙ ПФОПЫЕОЙК НЕЦДХ РТПУФЩНЙ УХЦДЕОЙСНЙ ЙУРПМШЪХЕФУС МПЗЙЮЕУЛЙК ЛЧБДТБФ:
I. пФОПЫЕОЙЕН РПДЮЙОЕОЙС УЧСЪБОЩ УХЦДЕОЙС б Й I, е Й п. пВЭЙЕ УХЦДЕОЙС (б Й е) СЧМСАФУС РПДЮЙОСАЭЙНЙ, Б ЮБУФОЩЕ (I, п) РПДЮЙОЕООЩНЙ. дМС УХЦДЕОЙК ОБИПДСЭЙИУС Ч ПФОПЫЕОЙЙ РПДЮЙОЕОЙС, ЙНЕЕФ ЪОБЮЕОЙЕ ХУМПЧЙЕ ЙУФЙООПУФЙ: еУМЙ ЙУФЙООП б(е), ФП ЙУФЙООП Й I(O), ОП ОЕ ОБПВПТПФ.
4. пРЕТБГЙЙ У РТПУФЩНЙ УХЦДЕОЙСНЙ (ОЕРПУТЕДУФЧЕООЩЕ ХНПЪБЛМАЮЕОЙС).
рТЙ РПНПЭЙ ПРЕТБГЙК ПВТБЭЕОЙС, РТЕЧТБЭЕОЙС Й РТПФЙЧПРПУФБЧМЕОЙС РПМХЮБАФУС ОПЧЩЕ УХЦДЕОЙС, ЬЛЧЙЧБМЕОФОЩЕ ЙУИПДОЩН.
уНЩУМ ПВТБЭЕОЙС ЛБЛ ПРЕТБГЙЙ ЪБЛМАЮБЕФУС Ч ФПН, ЮФП УХВЯЕЛФ Й РТЕДЙЛБФ УХЦДЕОЙС НЕОСАФУС НЕУФБНЙ (ПВТБЭБАФУС), ОЕ НЕОСС ЛБЮЕУФЧБ УХЦДЕОЙС.
еУМЙ ЛПМЙЮЕУФЧП РТЙ ЬФПН УПИТБОСЕФУС, ФП ЬФП УХЦДЕОЙЕ ВЕЪ ПЗТБОЙЮЕОЙС (РТПУФПЕ ЙМЙ ЮЙУФПЕ), ЕУМЙ ЛПМЙЮЕУФЧП ЙУИПДОПЗП УХЦДЕОЙС НЕОСЕФУС, ФП ЬФП УХЦДЕОЙЕ У ПЗТБОЙЮЕОЙЕН.
I. A→I
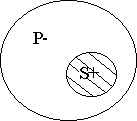
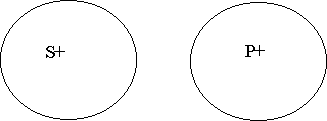
уХЦДЕОЙЕ б ПВТБЭБЕФУС Ч I У ПЗТБОЙЮЕОЙЕН (ПЗТБОЙЮЕОЙЕ УЧСЪБОП У ФЕН ЮФП РПОСФЙС S Й т ЧЪСФЩ Ч ТБЪОПН ПВЯЕНЕ, Ч ЬФПН МЕЗЛП ХВЕДЙФУС РТЙ РПНПЭЙ УИЕНЩ). чУЕ S ЕУФШ т
оЕЛПФПТЩЕ т ЕУФШ S
оБРТЙНЕТ: «еУМЙ ЧУЕ МАДЙ УНЕТФОЩ, ФП МЙЫШ ОЕЛПФПТЩЕ УНЕТФОЩЕ УХЭЕУФЧБ СЧМСАФУС МАДШНЙ» (еУМЙ ЧУЕ S ЕУФШ т, ФП ОЕЛПФПТЩЕ т ЕУФШ S). чПЪНПЦОП ПВТБЭЕОЙЕ б→б: еУМЙ ЧУЕ ЛЧБДТБФЩ(S) СЧМСАФУС ТБЧОПУФПТПООЙНЙ РТСНПХЗПМШОЙЛБНЙ, ФП ЧУЕ ТБЧОПУФПТПООЙЕ РТСНПХЗПМШОЙЛЙ(P) СЧМСАФУС ЛЧБДТБФБНЙ (S) (еУМЙ ЧУЕ S ЕУФШ т, ФП ЧУЕ т ЕУФШ S)
II. е→е
уХЦДЕОЙЕ е ПВТБЭБЕФУС Ч е ВЕЪ ПЗТБОЙЮЕОЙС
оБРТЙНЕТ: «еУМЙ ЧУЕ ФЕБФТЩ ОЕ СЧМСАФУС РПМЙЛМЙОЙЛБНЙ, ФП ЧУЕ РПМЙЛМЙОЙЛЙ ОЕ СЧМСАФУС ФЕБФТБНЙ». чУЕ S ОЕ-ЕУФШ т
чУЕ т ОЕ-ЕУФШ S
III. I→I
уХЦДЕОЙС I ПВТБЭБЕФУС Ч I ФБЛЦЕ ВЕЪ ПЗТБОЙЮЕОЙС.
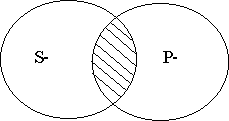
оЕЛПФПТЩЕ S ЕУФШ т
оЕЛПФПТЩЕ т ЕУФШ S
оБРТЙНЕТ: еУМЙ ОЕЛПФПТЩЕ УФХДЕОФЩ СЧМСАФУС УРПТФУНЕОБНЙ, ФП ОЕЛПФПТЩЕ УРПТФУНЕОЩ СЧМСАФУС УФХДЕОФБНЙ
IV. п→?
уХЦДЕОЙЕ п ОЕ ПВТБЭБЕФУС
4. юБУФОППФТЙГБФЕМШОЩЕ УХЦДЕОЙС (п) РХФЕН РТПФЙЧПРПУФБЧМЕОЙС УХВЯЕЛФХ, Ч УЙМХ ОЕПРТЕДЕМЕООПУФЙ ЛЧБОФПТБ «ОЕЛПФПТЩЕ», ОЕ РПЪЧПМСАФ ХЛБЪБФШ ЕДЙОУФЧЕООПЕ УМЕДУФЧЙЕ ЙЪ ЙУИПДОПЗП УХЦДЕОЙС.