Symbols that can be used to combine multiple boolean expressions into one boolean expression
Symbols that can be used to combine multiple boolean expressions into one boolean expression
Combine true/false expressions with and, or, and not for complex C# if statements
With if statements our program makes decisions while it runs. How advanced those decisions are depends on the if statement’s condition. Plenty of if statements evaluate a single Boolean expression. But for advanced logic we have to combine several true/false expressions into a single true or false value. Let’s see which C# operators make that possible.
IN THIS ARTICLE:
# Elaborate if statements that evaluate multiple Boolean expressions
But there are only so many situations we can process with a single Boolean expression. With complex programs we often have to check multiple values before we execute an if statement. So how do we evaluate multiple true/false expressions in an if statement condition?
To combine true/false expressions we use C#’s logical operators. Those operators, which are also called Boolean operators, combine several expressions into a single true or false value (Sharp, 2013; Stephens, 2014). This means logical operators combine several requirements into an if statement’s condition. That way they precisely control in which situation(s) our if statement’s code should run.
These are the logical operators that C# has (Liberty & MacDonald, 2009; Sharp, 2013; Stephens, 2014):
With if statements we often use the following logical operators:
# Advanced if statements with C#’s logical operators
Now let’s see how we can code if statements with the above logical operators.
# Example: if statement for two things at the same time
Here’s an if statement example:
Before the code of this if statement runs, the rpm variable has to be greater than ( > ) 0 while at the same time being less than ( ) 3,000. When the variable’s value is inside that range, the Console.WriteLine() method executes. When rpm is not bigger than 0 and/or less than 3,000, the && operator returns false and this if statement’s code doesn’t run.
# Example: if statement that checks if one of two things occurred
Here’s how an if statement can use the || operator:
# Example: if statement that checks if something didn’t happen
# Example: if/else statement with multiple true/false expressions
Of course, we can also use C#’s logical operators with other types of if statements. This if/else statement uses the logical AND operator ( && ) in its condition:
The if portion checks if the newMembers variable is greater than 50 and the appDownloads variable is bigger than 1,500. Since we combine those two expressions with the && operator, both have to be true before the if code block runs.
# Example: multiple logical operators in a single if statement
To evaluate complex conditions we often have to use multiple logical operators. Let’s consider this if statement for example:
We separate those two groups with the || operator. That means only one of them has to be true before the if statement’s code run, which makes the if statement evaluate two distinct situations. So when there are more then 225 new members and over 10,000 downloads, the if code runs. That code also executes when there are 100 or less new members and over 25,000 downloads.
# Tip: evaluate C#’s Boolean expressions with shorthand form
Here are some examples that use shorthand form to evaluate a true/false expression:
# Example: shorthand evaluation with C#’s if statements
The benefit of skipping the explicit test for true or false is that our code becomes shorter and easier to read. Say we have the following if statements:
A better way to write these if statements, and save a few key presses, is the following:
# Tip: use parentheses with complex if conditions
Once we use C#’s logical operators to make complex if statements, it’s a good idea to use parentheses ( ( and ) ). There are three reasons for that:
Let’s take a closer look at these benefits.
# Parentheses change how C# processes an if condition
With parentheses we change the order in which C# evaluates our logical condition. This is sometimes necessary to prevent mistakes. Say we have the following if statement:
But that’s not how C# evaluates this if statement. What C# does is is first combine the medianRPM and rpm > 0 expressions with the && operator. Then it uses the the || operator to combine that true/false outcome with the avgRPM expression. So in effect we combine the median RPM and RPM above zero with each other, and then look if the average is under 2,500.
That different order happens because the logical AND operator ( && ) has a higher priority than the logical OR operator ( || ) (Dorman, 2010; Liberty & MacDonald, 2009). That means && takes precedence over || in the same statement. Luckily there’s an easy way to change the order of operations: with parentheses ( ( and ) ) (Sharp, 2013). This works because C# always evaluates code inside the innermost group of parentheses first. And then it works its way out to the second innermost group of parentheses, and so on.
So to make our if statement evaluate the engine’s RPM correctly, we have to use parentheses to make the right way to evaluate the code explicit:
The two expressions that compare the avgRPM and medianRPM variables as arguments are now inside parentheses. That makes C# evaluate those with the || operator first. The true/false outcome of that is, with the && operator, combined with the rpm > 0 expression. This way our code first looks if the RPM is below its maximum level, and then see whether it’s above the minimum reading.
While C#’s order of operations is an important feature, there’s no need to memorise the order of operations – just use parentheses whenever you’re not exact sure of the right order. Those parentheses have the added bonus that they clarify your expressions. (It doesn’t affect your program when you use parentheses when they aren’t strictly speaking necessary.)
# Parentheses help spot common mistakes
Another reason to use parentheses with complex if statements that they help spot common mistakes. One of those mistakes happens when we combine two conditional tests with a logical operator, but only include the left-hand value once (Sharp, 2013).
An example of that error is:
When place each expression in its own pair of parentheses, errors like these are easier to spot:
The correct if statement is, of course, one that uses the avgRPM variable twice:
# Parentheses make an if condition easier to read
Parentheses also make complex if statements easier to read. While they do take a bit of time of type, that time is easily made up when you (or your teammates) have to read the code in the future.
Consider, for instance, the following if statement:
While this if statement runs correctly, the different expressions and their values don’t make for easy reading. But with parentheses, however, our code becomes much clearer:
This shows that even relatively simple if statements are easier to read and comprehend with parentheses.
# Summary
To have our program evaluate complex scenarios we often use several Boolean expressions in a single if statement. There are three logical operators we commonly use with those if statements.
Complex if statements are easier to code when we use parentheses. That makes code easier to read and prevents common mistakes. It also changes the order of operations to what we intended.
References
Dorman, S. (2010). Sams Teach Yourself Visual C# 2010 in 24 Hours. Indianapolis, IN: Sams/Pearson Education.
Liberty, J. & MacDonald, B. (2009). Learning C# 3.0: Master the Fundamentals of C# 3.0. Sebastopol, CA: O’Reilly Media.
Sharp, J. (2013). Microsoft Visual C# 2013 Step by Step. Microsoft Press.
Stellman, A. & Greene, J. (2010). Head First C#: A Brain-Friendly Guide (2nd edition). Sebastopol, CA: O’Reilly Media.
Stephens, R. (2014). C# 5.0 Programmer’s Reference. Indianapolis, IN: John Wiley & Sons.
Last updated on January 16, 2019 (published March 17, 2018 ).
# Related C# tutorials
C# can short-circuit true/false conditions that use the && or || logical operator. This way we make our if statements a bit more efficient.
Welcome on Kodify.net! This website aims to help people like you reduce their programming curve. I hope you find the articles helpful with your programming tasks.
Want to know more about me? Check out the about page.
See all TradingView tutorials to learn about a lot of Pine Script features
A «Feild» Guide to Programming with C++
Important takeaways
Contents
Overview
It is rare that we write a program that does exactly one thing every time it runs, never deviating from a strict set of steps. More commonly, we want to write programs that react to inputs from the user or another source and execute one piece of code or another given some condition about the current state of variables.
In \ref, we see a flowchart for an ATM system, where we get data from the user (their bank account number and the amount to withdraw from the account). Rather than just dispensing the money, we first check to ensure the user has sufficient funds in their account to make the withdraw. Based on the outcome of that check, we go down one of two paths: we either update the user’s account balance and make the withdraw, or we void the transaction and notify the user about the insufficient funds. We refer to each path as a branch of a program. Each branch contains a set of instructions that should only be executed under certain conditions, and when presented with several parallel branches, the computer can only take one.
In this chapter, we will learn about how to implement branching in C++ and how to construct the conditions (called Boolean expressions) to instruct the computer when to take a branch.
if statements
The simplest branch structure in C++ is the if statement. It works by running a specified block of code at a point in a program only if a given condition holds. If the condition does not hold, the block of code is skipped entirely.
Let’s see how to use if statements; say we want to read a number in from the user and, if the number is less than 10, we’ll print out a message. The code might look like this:
The general structure is:
Here are a few examples of Boolean expressions:
Back to the if statement above. Everything within the curly braces immediately following an if statement is the body of the branch. If the expression evaluates to true, then the block of code inside of the curly braces will be executed; if the expression evaluates to false, then the code inside the curly braces is skipped and will not be executed. The program will pick up just after the ending curly brace.
If the body consists of a single statement, the compiler does not require us to include the curly braces. For example, we can rewrite \ref as follows:
Be careful with this—sometimes programmers start off with no braces because there’s only one statement in the body, but then add another statement later and forget to add in the curly braces. This can cause hard-to-spot errors! It is strongly recommended that you always use curly braces to avoid such errors.
else statements
else if statements
Here is an updated version of \ref that uses an else if to print out an alternative message when the number provided by the user is exactly 10:
switch statements
I mentioned above that sometimes we want to leave break statements out so we can run the code in the following case statement. Below is an adaptation of \ref that is agnostic of the capitalization of the input character (so ‘k’ and ‘K’ are both valid to keep going, and ‘q’ or ‘Q’ are valid for quitting).
Complex Boolean expressions
Operator Precedence
Just as in algebra, you may override any order of precedent by using parentheses to group subexpressions. For more information about operator precedence (including operators will have not yet encountered), see this page.
De Morgan’s Laws
Turning back to our example, our if statement checks if the user’s input is in the valid range. What we really want is to check if it’s not in the valid range, and if so, exit the program. If the rating is valid, then the code that exits the program will be skipped and we can carry on doing whatever we want with the valid range. To do this, we have a couple of options.
De Morgan’s Laws. We can actually go from Option 1 to Option 2 algebraically by distributing the logical not into the expression. To do this, we use De Morgan’s Laws. The two laws say the following:
Note that x and y are placeholders for arbitrary expressions. We distribute the not to all subexpressions inside and flip the operator. In the case of test operators, we don’t distribute the not to the operands, but we do flip the operator as follows:
So, if we have the Boolean expression from method 1, we can distribute the not as follows:
Oracle AND Operator
Summary: in this tutorial, you will learn how to the Oracle AND operator to combine two or more Boolean expressions.
Introduction to Oracle AND operator
The AND operator is a logical operator that combines Boolean expressions and returns true if both expressions are true. If one of the expressions is false, the AND operator returns false.
The syntax of the AND operator is as follows:
The following table illustrates the result when you combine the true, false, and a NULL value using the AND operator
| TRUE | FALSE | NULL | |
|---|---|---|---|
| TRUE | TRUE | FALSE | NULL |
| FALSE | FALSE | FALSE | FALSE |
| NULL | NULL | FALSE | NULL |
When you use more than one logical operator in a statement, Oracle always evaluates the AND operators first. However, you can use parentheses to change the order of evaluation.
Oracle AND operator examples
See the following orders table in the sample database:
A) Oracle AND to combine two Boolean expressions example
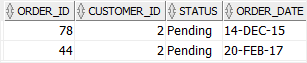
The following example finds orders of the customer 2 with the pending status:
In this example, the query returned all orders that satisfy both expressions:
Here is the result:
B) Oracle AND to combine more than two Boolean expressions example
You can use multiple AND operators to combine Boolean expressions.
For example, the following statement retrieves the orders that meet all the following conditions:
In this example, we used the EXTRACT() function to get the YEAR field from the order date and compare it with 2017.
C) Oracle AND to combine with OR operator example
You can combine the AND operator with other logical operators such as OR and NOT to form a condition.
For example, the following query finds order placed by customer id 44 and has status canceled or pending.
In this tutorial, you have learned how to use the Oracle AND operator to combine two or more Boolean expressions.
Boolean Expressions
A Boolean expression can consist of Boolean data, such as the following:
BOOLEAN variables or formulas
Functions that yield BOOLEAN results
BOOLEAN values calculated by comparison operators
For example, assume that your code contains the following Boolean expression.
Table 3-3, «Comparison and Logical Operators» shows the comparison and logical operators. Each operator has a priority that determines its order of evaluation. Operators of equal priority are evaluated left to right, unless parentheses change the order of evaluation. However, the evaluation is halted when the truth value is already decided. For example, in the following expression, the TOTAL function is never executed because the first phrase determines that the whole expression is true.
Creating Boolean Expressions
A Boolean expression is a three-part clause that consists of two items to be compared, separated by a comparison operator. You can create a more complex Boolean expression by joining any of these three-part expressions with the AND and OR logical operators. Each expression that is connected by AND or OR must be a complete Boolean expression in itself, even when it means specifying the same variable several times.
For example, the following expression is not valid because the second part is incomplete.
In the next expression, both parts are complete so the expression is valid.
When you combine several Boolean expressions, the whole expression must be valid even when the truth value can be determined by the first part of the expression. The whole expression is compiled before it is evaluated, so when there are undefined variables in the second part of a Boolean expression, you get an error.
Use the NOT operator, with parentheses around the expression, to reverse the sense of a Boolean expression.
The following two expressions are equivalent.
Example 3-1 Using Boolean Comparisons
The following example shows a report that displays whether sales in Boston for each product were greater than a literal amount.
This REPORT statement returns the following data.
Comparing NA Values in Boolean Expressions
Table 3-6, «Boolean Expressions with NA Values that Result in non-NA Values» shows the results of Boolean expressions involving NA values, which yield non-NA values.
Table 3-6 Boolean Expressions with NA Values that Result in non-NA Values
Symbols that can be used to combine multiple boolean expressions into one boolean expression
Implementing Logical Expressions
You’ve already seen several comparison operators. Below are many of the built-in operators:
Each of the comparison operators requires two operands, one on each side of the expression. For example:
To test if a value is between two numbers, you need to check the two conditions separately. The following is not a legal C# expression:
To combine multiple expression, you use logical operators.
Conditional Logical Operators
Conditional logical operators are used to combine multiple logical expressions. The most common logical operators are and, or, and not, which are represented as follows:
Note <.note>
C# also includes bitwise logical operators, & (AND), | (OR). These are used to perform binary comparisons of numeric values, and generally aren’t used directly for conditional expressions. The ^ (XOR) operator can be used with both boolean and integral operands.
Logical operations are applied left to right, and will short-circuit. That is, if the left operand of an && operator is false, the right operand will not be evaluated. This is often important, since the operands themselves may be method calls, not variables. You’ll learn more about methods in lesson 12.
Logical expressions are grouped using parentheses, which modify their order of operations just as in algebra. For example:
A boolean ( bool ) variable is often referred to as a flag. Flags can be useful as a means giving a name to a particular condition. For example: