What are the factors of 36
What are the factors of 36
Factors of 36
So you need to find the factors of 36 do you? In this quick guide we’ll describe what the factors of 36 are, how you find them and list out the factor pairs of 36 for you to prove the calculation works. Let’s dive in!
Want to quickly learn or show students how to find the factors of 36? Play this very quick and fun video now!
Factors of 36 Definition
When we talk about the factors of 36, what we really mean is all of the positive and negative integers (whole numbers) that can be evenly divided into 36. If you were to take 36 and divide it by one of its factors, the answer would be another factor of 36.
Let’s look at how to find all of the factors of 36 and list them out.
How to Find the Factors of 36
We just said that a factor is a number that can be divided equally into 36. So the way you find and list all of the factors of 36 is to go through every number up to and including 36 and check which numbers result in an even quotient (which means no decimal place).
Doing this by hand for large numbers can be time consuming, but it’s relatively easy for a computer program to do it. Our calculator has worked this out for you. Here are all of the factors of 36:
All of these factors can be used to divide 36 by and get a whole number. The full list of positive factors for 36 are:
1, 2, 3, 4, 6, 9, 12, 18, and 36
Negative Factors of 36
Technically, in math you can also have negative factors of 36. If you are looking to calculate the factors of a number for homework or a test, most often the teacher or exam will be looking for specifically positive numbers.
However, we can just flip the positive numbers into negatives and those negative numbers would also be factors of 36:
How Many Factors of 36 Are There?
As we can see from the calculations above there are a total of 9 positive factors for 36 and 9 negative factors for 36 for a total of 18 factors for the number 36.
There are 9 positive factors of 36 and 9 negative factors of 36. Wht are there negative numbers that can be a factor of 36?
Factor Pairs of 36
A factor pair is a combination of two factors which can be multiplied together to equal 36. For 36, all of the possible factor pairs are listed below:
We have also written a guide that goes into a little more detail about the factor pairs for 36 in case you are interested!
Just like before, we can also list out all of the negative factor pairs for 36:
Notice in the negative factor pairs that because we are multiplying a minus with a minus, the result is a positive number.
So there you have it. A complete guide to the factors of 36. You should now have the knowledge and skills to go out and calculate your own factors and factor pairs for any number you like.
Feel free to try the calculator below to check another number or, if you’re feeling fancy, grab a pencil and paper and try and do it by hand. Just make sure to pick small numbers!
Cite, Link, or Reference This Page
If you found this content useful in your research, please do us a great favor and use the tool below to make sure you properly reference us wherever you use it. We really appreciate your support!
«Factors of 36». VisualFractions.com. Accessed on August 15, 2022. http://visualfractions.com/calculator/factors/factors-of-36/.
«Factors of 36». VisualFractions.com, http://visualfractions.com/calculator/factors/factors-of-36/. Accessed 15 August, 2022.
Factors of 36. VisualFractions.com. Retrieved from http://visualfractions.com/calculator/factors/factors-of-36/.
Factors Calculator
Want to find the factor for another number? Enter your number below and click calculate.
Factors of 36
Factors of 36 are those numbers that divide 36 completely without leaving any remainder. There are 9 factors of 36 among which 36 is the biggest factor and 2 and 3 are its prime factors. The prime factorization of 36 can be done by multiplying all its prime factors such that the product is 36. Let us learn about all factors of 36, the prime factorization of 36, and the factor tree of 36 in this article.
| 1. | What are the Factors of 36? |
| 2. | Prime Factorization of 36 |
| 3. | Factor Tree of 36 |
| 4. | Factors of 36 in Pairs |
| 5. | FAQs on Factors of 36 |
What are the Factors of 36?
How to Find the Factors of 36?
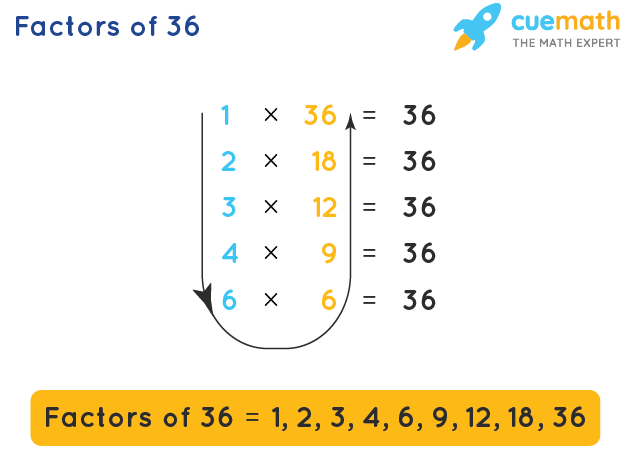
Factorization of a number means writing the number as a product of its factors. The most commonly used method to find the factors of a number is using the multiplication method. Let us find the factors of 36 using multiplication.
Factors of 36 using Multiplication
Let us find the factors of 36 using the multiplication method using the following steps.
Therefore, the factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, and 36. Now, let us learn about the prime factorization of 36.
Prime Factorization of 36
Prime factorization is a way of expressing a number as a product of its prime factors. The prime factors of a number are those factors that are prime numbers. The prime factorization of 36 can be done using the following steps. Observe the figure given below to understand the prime factorization of 36.
Therefore, the prime factors of 36 are 2 and 3 and the Prime factorization of 36 = 2 × 2 × 3 × 3
Factor Tree of 36
We can also find the prime factors of 36 using a factor tree. The factor tree of 36 can be drawn by factorizing 36 until we reach its prime factors. These factors are split and written in the form of the branches of a tree. The final factors are circled and are considered to be the prime factors of the 36. Let us find the prime factors of 36 using the following steps and the factor tree given below.
Note: It should be noted that there can be different factor trees of 36. For example, we can start by splitting 36 into 4 and 9. Then, 4 can be split further into 2 and 2, while 9 can be split into 3 and 3. Finally, we can observe the same prime factors, that is, 36 = 2 × 2 × 3 × 3
Factors of 36 in Pairs
The factors of 36 can be written in pairs. This means that the product of the pair factors of 36 is always 36.The factors of 36 in pairs can be written as shown in the table given below:
| Factors | Positive Pair Factors |
| 1 × 36 = 36 | 1, 36 |
| 2 × 18 = 36 | 2, 18 |
| 3 × 12 = 36 | 3, 12 |
| 4 × 9 = 36 | 4, 9 |
| 6 × 6 = 36 | 6, 6 |
It is possible to have negative pair factors as well because the product of two negative numbers also gives a positive number. Let us have a look at the negative pair factors of 36.
The following points explain some features of the pair factors of 36.
Important Notes
Points to remember
Let us recollect the list of the factors, the negative factors, and the prime factors of 36.
☛ Related Articles
Examples on Factors of 36
Example 1: State true or false with respect to the factors of 36.
a.) 3 and 6 are factors of 36.
b.) 2 and 3 are the prime factors of 36.
Solution:
a.) True, 3 and 6 are factors of 36.
b.) True, 2 and 3 are the prime factors of 36.
Example 2: Write all the positive factors of 36.
Solution:
All the positive factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Example 3:
List the positive and negative pair factors of 36.
Solution:
Factors of 36
What are the Factors of 36?
Factors of a number are the product of such numbers which completely divide the given number. Factors of a given number can be either positive or negative numbers. By multiplying the factors of a number we get the given number. For example 1, 2, 3, 6 are the factors of 6. On multiplying two or more numbers we get 6. Hence we have 2 x 3 = 6 or 1 x 6 = 6. On this page, we will study the factors of 36 definitions, how to find the factors of 36 and examples.
Prime Number
Prime numbers are whole numbers that are divisible by the number 1 and the number itself. So they have just two factors. For example 2,3,5,7,11… are the beginning prime numbers. 1 is neither a prime number nor a composite number. The prime number was discovered by Eratosthenes in around 275-194 B.C. He took the example of a sieve to filter out the prime numbers and drain out composite numbers from a list of natural numbers.
Co-Prime Numbers
Two numbers are said to be co-prime or mutually prime if and only if their common factor or only positive integer that is divisor for both of them is 1. In other words, their highest common factor is always 1.
For example, 21 and 22.
Factors of 21 are 1, 3, 7, 21 and factors of 22 are 1, 2, 11 and 22.
Facts about Prime Numbers
Prime numbers between 1 and 100 are more than the prime numbers between 101-200.
The only even Prime number is 2, the rest of the prime numbers are odd.
Two numbers are always coprime to one another.
No prime number which is greater than 5 ends with the number 5.
Factors of 36
The factors of the number 36 are the numbers that are multiplied together to get the original number 36. Since the number 36 is a composite number and not a prime number, there are many other factors besides the 1 and the number itself. Therefore, the 36 elements are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
Prime Factor and Prime Factorisation of Number 36
36 is divisible by the prime number 2 and becomes 18. If you repeat the same procedure again, the resulting value will be 9. Furthermore, 9 is divisible by the prime number 3, and the result after division is 3 which is a prime number and cannot be divided any further. number. Therefore, the prime factors of 36 are 2, 2, 3, and 3.
The method of writing a number as the product of 36 prime factors is called the 36 prime factorizations. To find the 36 prime factors, divide them by the smallest prime number, 2. If it cannot be further divided by 2, divide by the next prime number, 3, and continue this process until the final product is 1. This is called the prime factorization of numbers, and the 36 increments are shown below.
Step 1: Divide 36 with 2
Step 2: Again divide 18 with 2
Step 3: Since 9 is not divisible by 2, our next prime number is 3
Step 4: Finally at the last step divide 3 with 3 to get 1.
We can see here that the prime factors of 36 will be 2 × 2 × 3 × 3 i.e. 2^2 × 3^2.
Factors of 36 Definition
We know that the factor of a number divides the number completely if we talk about the number 36, the number 36 is composite and it can be presented as a unique product of primes, which is actually prime factorization. There is more than one factor for a number like 36; however, there is always one way of representing the number as a product of prime which is why prime factorization is called a unique product of primes. Now, let’s write the various factors of 36:
= 12 x 3 or 3 x 12
So, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
How to Find the Factors of 36?
According to the definition of factors of 36 we know that factors of 36 are all the positive or negative integers which divide the number 36 completely. So let us simply divide the number 36 by every number which completely divides 36 in ascending order till 36.
So the factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, and 36.
We know that factors also include negative integers hence we can also have,
Factors of 36 Can be Listed as Follows:
Positive Factors of 36
1, 2, 3, 4, 6, 9, 12, 18, and 36
Negative Factors of 36
– 1, – 2, – 3, – 4, – 6, – 9, – 12, – 18, and – 36
Hence 36 have a total 9 positive factors and 9 negative factors.
Factors Pairs of 36
Factor Pairs of 36 are combinations of two factors that when multiplied together give 36.
List of all the Positive Factor Pairs of 36
As we know that Factors of 36 include negative integers too.
List of all the Negative Factor Pairs of 36:
Prime Factors of 36
According to the prime factor definition we know that the prime factor of a number is the product of all the factors that are prime( a number that divides by itself and only one). Hence we can list the prime factors from the list of factors of 36.
Or the other way to find the prime factorization of 36 is by prime factorization or by factor tree.
How To Calculate Prime Factorization of 36?
To calculate the prime factorization of 36, first, take the least prime number that is 2. Divide it by 2 until it is completely divisible by 2. If at a point it is not divisible by 2 take the next least prime number that is 3. Perform the same steps and move forward, till we get 1, as the quotient. Here is the stepwise method to calculate the prime factors of 36
Step 1: Divide 36 with 2
Step 2: Again divide 18 with 2
Step 3: Now 9 is no more divisible by 2, move to the next prime number i.e. 3
Step 4: At last, divide 3 with 3 to get 1.
Here is the factor tree representing prime factors of 36.
Solved Examples:
Example 1: Write down the factors of 16.
Therefore the factors of 16 are 1, 2, 4, 8 and 16.
Example 2: Write down the factors of 68.
Therefore the factors of 16 are 1, 2, 4, 17, 34 and 68.
Example 3: If 144 is One of the Multiples of 36, then Write its Factors.
The factors of 72 are the same, with additional factors of 72 and 144. We can write the factor of 72 as 1, 2, 3, 4, 6, 9, 12, 18, 36, 72, and 144.
What are the factors of 36
We have all the information you will ever need about the Factors of 36. We will provide you with the definition of Factors of 36, show you how to find the Factors of 36, give you all the Factors of 36, tell you how many Factors 36 has, and supply you with all the Factor Pairs of 36 to prove that our answer is solved correctly.
Factors of 36 definition
The Factors of 36 are all the integers (positive and negative whole numbers) that you can evenly divide into 36. 36 divided by a Factor of 36 will equal another Factor of 36.
How to find the Factors of 36
Since the Factors of 36 are all the numbers that you can evenly divide into 36, we simply need to divide 36 by all numbers up to 36 to see which ones result in an even quotient. When we did that, we found that these calculations resulted in an even quotient:
36 Г· 1 = 36
36 Г· 2 = 18
36 Г· 3 = 12
36 Г· 4 = 9
36 Г· 6 = 6
36 Г· 9 = 4
36 Г· 12 = 3
36 Г· 18 = 2
36 Г· 36 = 1
The Postive Factors of 36 are therefore all the numbers we used to divide (divisors) above to get an even number. Here is the list of all Postive Factors of 36 in numerical order:
1, 2, 3, 4, 6, 9, 12, 18, and 36.
Factors of 36 include negative numbers. Therefore, all the Positive Factors of 36 can be converted to negative numbers. The list of Negative Factors of 36 are:
How many Factors of 36?
When we counted the Factors of 36 that we listed above, we found that 36 has 9 Positive Factors and 9 Negative Factors. Thus, the total number of Factors of 36 is 18.
Factor Pairs of 36
Factor Pairs of 36 are combinations of two factors that when multiplied together equal 36. Here are all the Positive Factor Pairs of 36
1 Г— 36 = 36
2 Г— 18 = 36
3 Г— 12 = 36
4 Г— 9 = 36
6 Г— 6 = 36
9 Г— 4 = 36
12 Г— 3 = 36
18 Г— 2 = 36
36 Г— 1 = 36
Like we said above, Factors of 36 include negative numbers. Minus times minus equals plus, thus you can convert the Positive Factor Pair list above by simply putting a minus in front of every factor to get all the Negative Factor Pairs of 36:
Factor Calculator
Do you need the factors for a particular number? You can submit a number below to find the factors for that number with detailed explanations like we did with Factors of 36 above.
Factors of 37
We hope this step-by-step tutorial to teach you about Factors of 36 was helpful. Do you want to see if you learned something? If so, give the next number on our list a try and then check your answer here.
The Factors Of 36
Alex Bolano PRO INVESTOR


What are the factors of 36? If you remember any high school math then that question probably was not that hard (the answer is 1, 2, 3, 4, 6, 9, 12, 18, and 36). Just in case though, let’s go over exactly what a factor is.
Factoring, or factorization, is the process by which a mathematical expression is rewritten as the product of simpler mathematical expressions. The elements that multiply together to equal the more complex expression are called that expression’s factors. In other words, the factors of some number N are the numbers that you can multiply together to equal N.
“Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding.” — William Paul Thurston
So with our original question, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36 because 1 × 36 = 36, 2 × 18 = 36, 3 × 12 = 36, 4 × 9 = 36, and 6 × 6 = 36. Similarly, the factors of 16 are 1, 2, 4, 8, and 16; and the factors of 21 are 1, 3, 7, and 21. Some numbers, like 23, are unique in that they only have 2 factors, 1 and themselves. These numbers are called prime numbers and they have some very special properties.
Numbers are not the only things that can have factors. Algebraic expressions, like x 2 −5x+6, have factors as well. Specifically, the factors of x 2 −5x+6 are simpler expressions (x−2) and (x−3). One can multiply (x−2) by (x−3) to get x 2 −5x+6 and so they count as its factors.
Mathematical Properties Of Factors
Immediately, one can start to see some patterns that arise with factors. For example, every even number has 2 as a factor. Consequently, no even number can be prime, as they always have more factors than just one and themselves (except for the number 2 itself, which is notable for being the sole even prime number).
For all numbers N, the largest factor, aside from N itself, is less than or equal to half of N. This is because there is no number greater than half of N that you can multiply to equal N. Also, notice that all numbers can be written as the product of some set of prime numbers. For example, 27 can be expressed 27= 3×9 = 3×3 2 = 3×3×3. The expression 3×3×3 is the prime factorization of 27. The existence of prime factorizations is a consequence of the fundamental theorem of arithmetic, the fact that every number greater than 1 is either prime itself, or is the product of some prime numbers.
“Math is the language of the universe. So the more equations you know, the more you can converse with the cosmos.” — Neil DeGrasse Tyson
Not every expression can be factored, though. Expressions that cannot be factored are called irreducible polynomials and are said to be in their simplest form. Irreducible polynomials cannot be written as the product and any simpler elements. Whether or not a polynomial is irreducible is relative to a specific domain. x 2 −2 = (x−√2)(x+√2) is irreducible over the domain of the integers, as it cannot be written as the product of any 2 integers (√2 is not an integer). x 2 −2 = (x−√2)(x+√2) however, is reducible with respect to the real numbers, as √2 is a real number. Some polynomials are absolutely irreducible; that is irreducible across every domain of numbers. For example, the polynomial x n +y n −1 (sometimes called the Fermat curve) is irreducible for any positive number n. This means that it is impossible to express x n +y n −1 as the product of any two mathematical objects.
Applications Of Factoring
Factoring has a number of uses in calculus, physics, algebra, trig, and more complex mathematics. Primarily, factoring allows one to simplify a complex expression and rewrite as the product of simpler parts. In doing so, often one can highlight mathematical relationships otherwise hidden.
Here is an example: say we have the messy expression 4 √162. To simplify this we can factor the expression and get 4 √(3×3×3×3×2) = 4 √(3 4 ×2) = 3 4 √2. 3 4 √2 is much easier to deal with than 4 √162, and so factoring has saved us a huge headache.
Alternatively, factoring can be useful in situations where one is attempting to model real-world phenomena with mathematics. Let’s say I am tossing bowling balls off of the Leaning Tower of Pisa (Galileo would be proud). The motion of each bowling ball with respect to time can be represented by the equation ƒ(x)=−x 2 +x+6.
“Pure mathematicians just love to try unsolved problems – they love a challenge.” — Andrew Wiles
Additionally, factoring, or more specifically the difficulty of factoring extremely large numbers, plays a role in cryptography. Essentially, encrypted messages contain both a “public key” and a “secret key.” The public key consists of a number that is the product of two large prime numbers and is used to initially encrypt the message. The secret key consists of those two prime factors and is necessary to decrypt the message. Extremely large numbers are very difficult to factor into primes, so unless one already knows the secret key, it is practically impossible to break the encryption given the current state of computer technology. In fact, given the current state of computing technology, if one tried to brute force break a common 128-bit encryption, it would take about 2 66 seconds to test all possible combinations. To be clear, that is equivalent to about 2, 158 000, 000, 000 years—150 times the current age of the universe (
Factoring is one of the most basic and useful mathematical operations. In fact, recent studies show that relatively simple mathematical techniques, like factoring, are more useful to aiding mathematical understanding than more complex mathematical concepts. Factoring has useful applications all across the industry, so next time you are in math class make sure to pay attention.
About Alex Bolano PRO INVESTOR
When Alex isn’t nerdily stalking the internet for science news, he enjoys tabletop RPGs and making really obscure TV references. Alex has a Masters’s degree from the University of Missouri-St. Louis.