What is a polyconic projection based on
What is a polyconic projection based on
Polyconic projection
The projection is defined by:
: x = cot(phi) sin(lambda sin(phi)),
References
External links
Look at other dictionaries:
Polyconic projection — Polyconic Pol y*con ic, a. [Poly + conic.] Pertaining to, or based upon, many cones. [1913 Webster]
polyconic projection — [päl΄i kän′ik] n. a type of conic map projection in which the parallels are represented as arcs of circles having centers at different points along the straight central meridian and the other meridians are shown as curves … English World dictionary
polyconic projection — A map projection that is a combination of separate conic projections drawn for each parallel or latitude. In this projection, the central meridian is a straight line and other meridians are curves concave to the central meridians. Parallels are… … Aviation dictionary
polyconic projection — noun a conic projection of a map having distances between meridians equal to those distances on a globe • Hypernyms: ↑conic projection, ↑conical projection * * * noun : a map projection based on the development of a series of concentric cones… … Useful english dictionary
polyconic projection — noun Date: circa 1864 a map projection consisting of a composite series of concentric cones each of which before being unrolled has been placed over a sphere so as to be tangent to a different parallel of latitude … New Collegiate Dictionary
polyconic projection — Cartog. a conic projection in which the parallels are arcs of circles that are not concentric but are equally spaced along the central straight meridian, all other meridians being curves equally spaced along the parallels. [1900 05] * * * … Universalium
polyconic projection — pol•y•con′ic projec′tion [[t]ˌpɒl iˈkɒn ɪk[/t]] n. geo a conic map projection in which the parallels are arcs of circles that are not concentric but are equally spaced along the central straight meridian, all other meridians being curves equally… … From formal English to slang
international modified polyconic projection — A modified polyconic map projection chosen by an international committee in 1909 for construction of maps of the whole world, except polar caps, on one projection and on a scale of 1:1,000,000. The size of the sheet is 4° change of latitude by 6° … Aviation dictionary
Polyconic — Pol y*con ic, a. [Poly + conic.] Pertaining to, or based upon, many cones. [1913 Webster]
Polyconic
In this topic
Description
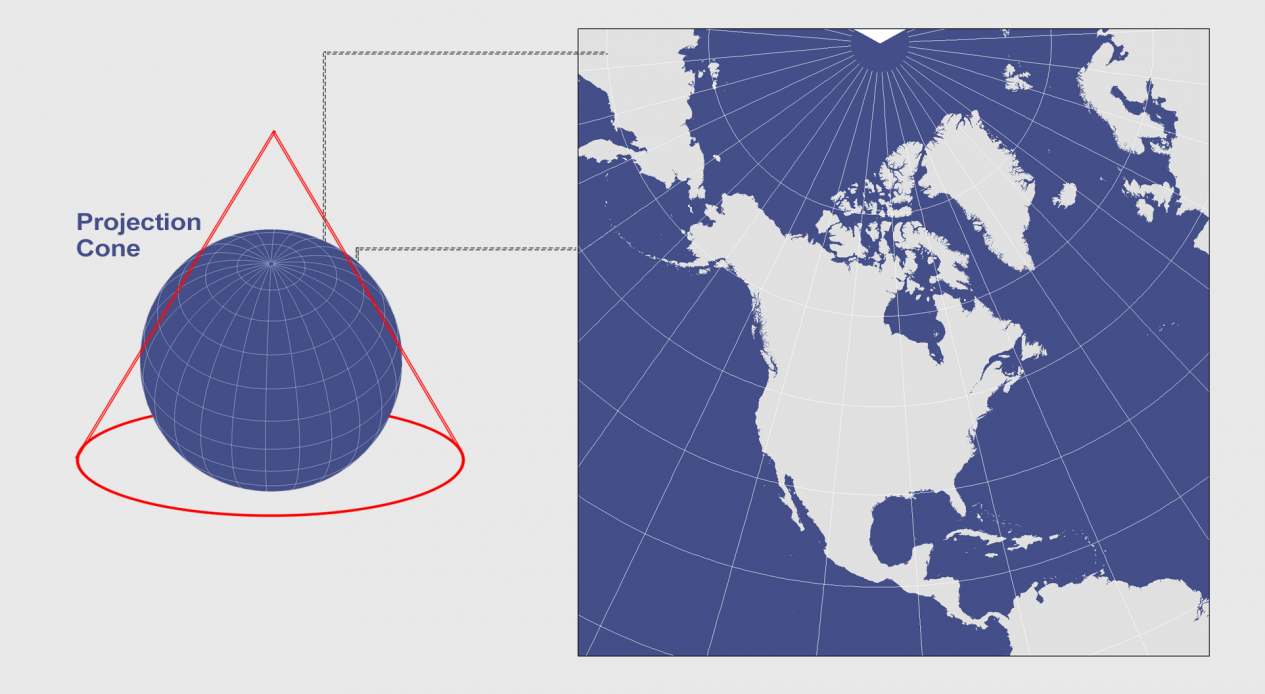
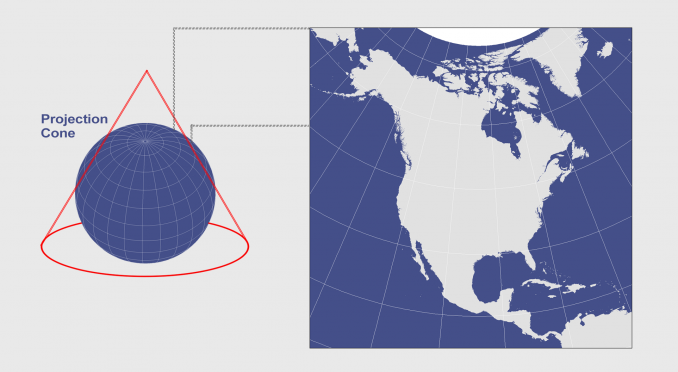
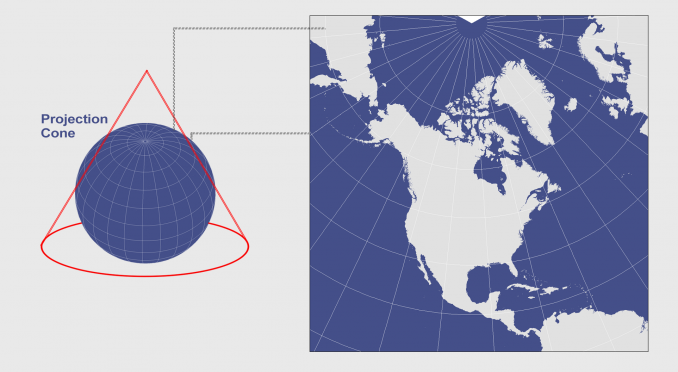
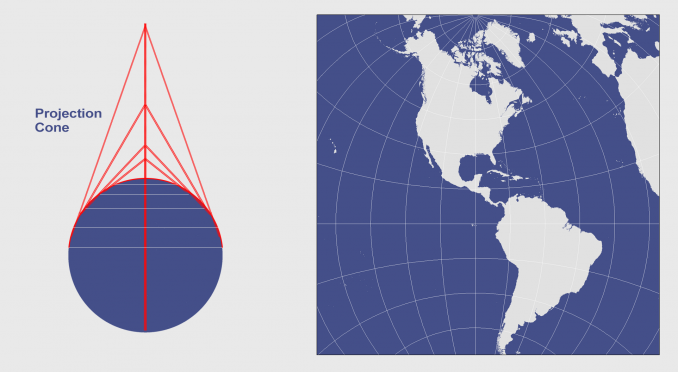
The polyconic projection is also known as American polyconic or ordinary polyconic projection. The name translates into «many cones,» and it is created by lining up an infinite number of cones along the central meridian. This affects the shape of the meridians. Unlike other conic projections, the meridians are curved rather than straight. The projection is neither conformal nor equal-area. It is appropriate for regions of predominant north-south extent.
The projection was developed by Ferdinand R. Hassler in 1820. It is available in ArcGIS Pro 1.0 and later and in ArcGIS Desktop 8.0 and later.

Projection properties
The subsections below describe the polyconic projection properties.
Graticule
This is a polyconic projection. The equator and the central meridian are projected as two perpendicular straight lines. All other meridians are complex curves, equally distributed along the equator and each parallel of latitude and concave toward the central meridian. All the parallels are nonconcentric circular arcs, equally distributed along the central meridian. The poles are presented as points. The graticule is symmetric across the equator and the central meridian.
Distortion
The polyconic projection is neither conformal nor equal-area. It generally distorts shapes, areas, distances, directions, and angles. The central meridian is free of distortion. The scale along each parallel and along the central meridian of the projection is accurate. Distortion increases with distance from the central meridian. The east-west distortion is greater than north-south distortion. The projection produces considerable distortion toward the edge of the map. Distortion values are symmetric across the equator and the central meridian.
Usage
The polyconic projection is not recommended for regional maps. Because there is no distortion along the central meridian, the projection is appropriate for regions of predominant north-south extent. It was used for topographic USGS quad sheets from 1886 until approximately 1957.
Parameters
Sources
Snyder, J. P. (1987). Map Projections: A Working Manual. U.S. Geological Survey Professional Paper 1395. Washington, DC: United States Government Printing Office.
Snyder, J. P. (1993). Flattening the Earth. Two Thousand Years of Map Projections. Chicago and London: University of Chicago Press.
ArcMap
Description
The polyconic projection is also known as American polyconic or ordinary polyconic projection. The name translates into «many cones,» and it is created by lining up an infinite number of cones along the central meridian. This affects the shape of the meridians. Unlike other conic projections, the meridians are curved rather than straight. The projection is neither conformal nor equal-area. It is appropriate for regions of predominant north-south extent.
The projection was developed by Ferdinand R. Hassler in 1820. It is available in ArcGIS Pro 1.0 and later and in ArcGIS Desktop 8.0 and later.

Projection properties
The subsections below describe the polyconic projection properties.
Graticule
This is a polyconic projection. The equator and the central meridian are projected as two perpendicular straight lines. All other meridians are complex curves, equally distributed along the equator and each parallel of latitude and concave toward the central meridian. All the parallels are nonconcentric circular arcs, equally distributed along the central meridian. The poles are presented as points. The graticule is symmetric across the equator and the central meridian.
Distortion
The polyconic projection is neither conformal nor equal-area. It generally distorts shapes, areas, distances, directions, and angles. The central meridian is free of distortion. The scale along each parallel and along the central meridian of the projection is accurate. Distortion increases with distance from the central meridian. The east-west distortion is greater than north-south distortion. The projection produces considerable distortion toward the edge of the map. Distortion values are symmetric across the equator and the central meridian.
Usage
The polyconic projection is not recommended for regional maps. Because there is no distortion along the central meridian, the projection is appropriate for regions of predominant north-south extent. It was used for topographic USGS quad sheets from 1886 until approximately 1957.
Parameters
Sources
Snyder, J. P. (1987). Map Projections: A Working Manual. U.S. Geological Survey Professional Paper 1395. Washington, DC: United States Government Printing Office.
Snyder, J. P. (1993). Flattening the Earth. Two Thousand Years of Map Projections. Chicago and London: University of Chicago Press.
Conic Projection: Lambert, Albers and Polyconic
Conic Projection Examples
When you place a cone on the Earth and unwrap it, this results in a conic projection.
Some of the popular conic projections are Albers Equal Area Conic and the Lambert Conformal Conic projections.
Both of these types of map projections are well-suited for mapping long east-west regions because distortion is constant along common parallels. But they aren’t terribly good at projecting the whole planet.
Here are some details on conic projections and how maps use them today.
Albers Equal Area Conic Projection
The Albers Equal Area Conic projection is commonly used for displaying large countries that require equal-area representation. For example, the USGS uses this conic projection for maps showing the conterminous United States (48 states).
H. C. Albers introduced this map projection in 1805 with two standard parallels (secant). As the name states, the purpose was to project all areas on the map proportionally to all areas on Earth.
Albers Equal Area Conic Projection Distortion
Like all projections, the Albers Equal Area Conic Projection has map distortion. Distances and scale are true only on both standard parallels with directions being reasonably accurate. Areas are equal to the same areas on Earth, though it’s not conformal, perspective, or equidistant.
Lambert Conformal Conic Projection
The Lambert Conformal Conic is one of the many creations by Lambert in 1772 still widely used in the United States today. It looks like the Albers Equal Area Conic, but graticule spacings differ so that it’s conformal rather than equal area.
It uses a conic developable surface secant at two standard parallels, usually at 33° and 45° to minimize distortion. However, standard parallels vary depending on location. For example, Canada’s standard parallels are usually 49ºN. and 77ºN.
Furthermore, the State Plane Coordinate System (SPCS) uses LCC when zones have an east-west orientation.
Lambert Conformal Conic Projection Map Properties
The major advantage of the Lambert Conformal Conic map projection is how it retains conformality.
Despite how distances are reasonably accurate and retained along standard parallels, it isn’t equal area as distortion increases away from standard parallels.
Polyconic Projection
This now obsolete map projection uses an infinite number of cones tangent to an infinite number of parallels. This type of protection is generally used for countries that span along a longitudinal extent.
In a polyconic projection, all meridians except the central one have curved lines. Only along the central meridian, distances, direction, shape, and areas are true. However, distortion increases away from its central meridian.
Polyconic Projection Distortion
Overall, this map projection compromises many properties. It is neither conformal, perspective, or equal area.
Conic Projection Advantages and Disadvantages
Unlike cylindrical maps, conic map projections are generally not well-suited for mapping very large areas. They are more suitable for mapping continental and regional areas. For example, Albers Equal Area Conic and LCC are common for mapping the United States.
Polar orientation conic projections have their cone center point directly above the pole. Meridians are straight converging at the pole. Parallels are arcs circling the pole. Parallels cross meridians at right angles.
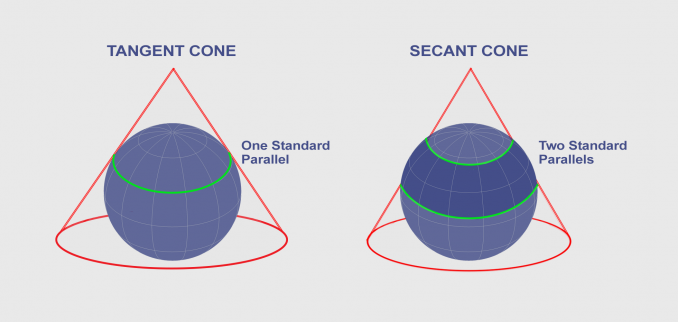
Tangent cones result in one standard line where the scale on that line has no distortion. Secant cones cut distortion down with two standard lines. These standard lines have no distortion but it increases away from these lines.
Additional Resources
Here are some more helpful references for map projection types:
polyconic projection
Тематики
Обобщающие термины
Синонимы
Тематики
Смотреть что такое «polyconic projection» в других словарях:
Polyconic projection — Polyconic Pol y*con ic, a. [Poly + conic.] Pertaining to, or based upon, many cones. [1913 Webster]
polyconic projection — [päl΄i kän′ik] n. a type of conic map projection in which the parallels are represented as arcs of circles having centers at different points along the straight central meridian and the other meridians are shown as curves … English World dictionary
Polyconic projection — A polyconic projection is a conical map projection. The projection stems from rolling a cone tangent to the Earth at all parallels of latitude, instead of a single cone in a normal conic projection. Each parallel is a circular arc of true scale.… … Wikipedia
polyconic projection — A map projection that is a combination of separate conic projections drawn for each parallel or latitude. In this projection, the central meridian is a straight line and other meridians are curves concave to the central meridians. Parallels are… … Aviation dictionary
polyconic projection — noun a conic projection of a map having distances between meridians equal to those distances on a globe • Hypernyms: ↑conic projection, ↑conical projection * * * noun : a map projection based on the development of a series of concentric cones… … Useful english dictionary
polyconic projection — noun Date: circa 1864 a map projection consisting of a composite series of concentric cones each of which before being unrolled has been placed over a sphere so as to be tangent to a different parallel of latitude … New Collegiate Dictionary
polyconic projection — Cartog. a conic projection in which the parallels are arcs of circles that are not concentric but are equally spaced along the central straight meridian, all other meridians being curves equally spaced along the parallels. [1900 05] * * * … Universalium
polyconic projection — pol•y•con′ic projec′tion [[t]ˌpɒl iˈkɒn ɪk[/t]] n. geo a conic map projection in which the parallels are arcs of circles that are not concentric but are equally spaced along the central straight meridian, all other meridians being curves equally… … From formal English to slang
international modified polyconic projection — A modified polyconic map projection chosen by an international committee in 1909 for construction of maps of the whole world, except polar caps, on one projection and on a scale of 1:1,000,000. The size of the sheet is 4° change of latitude by 6° … Aviation dictionary
Polyconic — Pol y*con ic, a. [Poly + conic.] Pertaining to, or based upon, many cones. [1913 Webster]