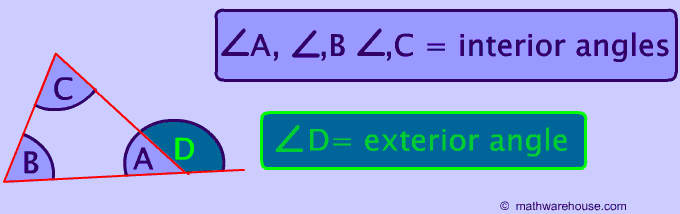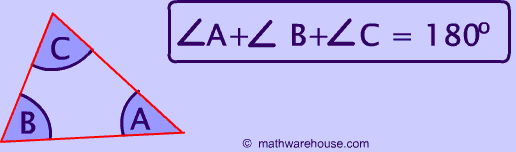What is angle side angle
What is angle side angle
The AAS (Angle-Angle-Side) Theorem
The AAS (Angle-Angle-Side) Theorem
Mathematics is a pure science, so you are almost never stopped on the street and challenged to test two triangles for congruence. If you were, though, you could test triangles for congruence in five ways. Knowing as many methods as possible helps you, giving you flexibility to deal with any situation, whether you are stopped on the street or stumped in the classroom. This method is the Angle Angle Side, or AAS Theorem.
Proving Congruent Triangles
Five methods exist for testing congruence in triangles, though one is restricted for use with right triangles. Here are all five:
In other lessons we have illustrated the other methods, and no, we did not just randomly rearrange «Angle» and «Side» in as many ways as we could think of. Notice, for instance, you cannot find Angle Angle Angle as a congruence proof (that is reserved for similarity), nor can you cook up a Side Side Angle postulate.
Whichever term you see sandwiched between the others, that part is included. An included angle or side is physically between the others in the triangle. So Side Angle Side (SAS) means one side, the angle next to that side, and then the side next to that angle. That side is out there, all alone, not between the angles.
For every testing method, you are checking the three parts identified between the two triangles. If corresponding parts are congruent for those three parts, the two triangles are congruent. These testing methods or proofs allow you to establish congruence by checking only half the parts (from three possible sides and three possible angles).
AAS Theorem
Your textbook probably calls this a theorem, or it may be labeled a postulate; don’t worry about it! Keep the concept, not the fussy words, in mind as you attempt to prove triangles congruent.
AAS Theorem Definition
Notice how it says «non-included side,» meaning you take two consecutive angles and then move on to the next side (in either direction). You do not take the side between those two angles! (If you did, you would be using the ASA Postulate).
The congruent parts are:
We know from these triangles that two interior angles are congruent (and consecutive, or next to each other), but we know nothing about the side between them. Instead, seemingly unhelpfully, we learn that another side is congruent.
Going through our toolbox full of triangle congruence testing methods, we can try each:
Why does the AAS Theorem work?
Quick, what do the interior angles of all triangles add up to?
If two angles and their included side of one triangle are all congruent to two corresponding angles and their included side of another triangle, the two triangles are congruent.
AAS Theorem Example
S i d e L G ≅ S i d e A M
Knowing the interior angles are congruent as listed, what else do you know?
What does that allow you to do now? Deploy ASA and declare the two triangles congruent, since:
S i d e L G ≅ S i d e A M
What Real Geometricians Do
You have no need of proving the third angle’s congruence and then deploying ASA, since we have, ready and waiting, the AAS Theorem. So real mathematicians and geometricians just leap right to AAS and declare the two triangles congruent.
If you have to explain this theorem to another student, friend, or random stranger on the street, you cannot make the leap from two angles to the mysterious third angle without some explanation. Then you may need to explain how we are essentially giving up on one of our original angles in favor of the third angle.
It is that mental shift, from a given angle to the newly identified third angle, that allows you to tap the awesome power of ASA and gather our previously outlying side into the proof.
Finally, after walking your pal through those steps, hit ’em with the efficiency and even more awesome power of AAS, where any two angles and a non-included side can be used to identify congruence between triangles. Pretty impressive, isn’t it?
Lesson Summary
Now that you have tinkered with triangles and studied these notes, you are able to recall and apply the Angle Angle Side (AAS) Theorem, know the right times to to apply AAS, make the connection between AAS and ASA, and (perhaps most helpful of all) explain to someone else how AAS helps to determine congruence in triangles.
Next Lesson:
What you’ll learn:
After studying these instructions and viewing the video, you will be able to:
Triangles Side and Angles
Interior & Exterior Angles and sides
Properties of Triangles
Triangles are one of the most fundamental geometric shapes and have a variety of often studied properties including:
What’s the difference between interior and exterior angles of a triangle?
This question is answered by the picture below. You create an exterior angle by extending any side of the triangle.
Interior Angles of a Triangle Rule
To explore the truth of this rule, try Math Warehouse’s interactive triangle, which allows you to drag around the different sides of a triangle and explore the relationship between the angles and sides. No matter how you position the three sides of the triangle, the total degrees of all interior angles (the three angles inside the triangle) is always 180°.
This property of a triangle’s interior angles is simply a specific example of the general rule for any polygon’s interior angles.
Interior Angles Interactive Demonstration
Practice Problems (interior angles rule)
Problem 1
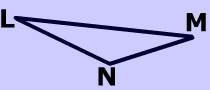
What is m$$\angle$$LNM in the triangle below?
Problem 2
In any triangle
To explore the truth of the statements you can use Math Warehouse’s interactive triangle, which allows you to drag around the different sides of a triangle and explore the relationships betwen the measures of angles and sides. No matter how you position the three sides of the triangle, you will find that the statements in the paragraph above hold true.
Angle Side Angle
Angle-Side-Angle is also called ASA criterion which means if two triangles are congruent any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle. Angle side angle is one of the conditions for two triangles to be congruent. The other conditions are SSS, SAS, AAS, and RHS. In this section, we will explore the ASA rule, the formula, and the congruence theorem using real-life examples.
| 1. | Definition of Angle Side Angle |
| 2. | Angle Side Angle Congruence Rule |
| 3. | Angle Side Angle Congruence Rule Proof |
| 4. | How to Apply Angle Side Angle Congruence Rule? |
| 5. | Angle Side Angle Congruence Theorem |
| 6. | Angle Side Angle Formula |
| 7. | FAQs on Angle Side Angle |
Definition of Angle Side Angle
By definition, an angle side angle states that if two angles of one triangle, and the side between these two angles, are respectively equal to the two angles and the side between the angles of another triangle, then the two triangles will be congruent to each other by ASA rule. Two triangles are said to be congruent when:
However, in order to be sure that two triangles are congruent, we do not necessarily need to have information about all sides and all angles. Let us understand ASA with an example. Consider the following two triangles, Δ ABC and Δ DEF:
We are given that,
BC = EF
∠B = ∠E
∠C = ∠F
We say that by ASA criterion: Δ ABC ≅ ΔDEF.
Angle Side Angle Congruence Rule
ASA Congruence rule states that two triangles are said to be congruent if any two angles and the side included between them of one triangle are equal to the corresponding angles and the included side of the other triangle. Look at the image given below to determine if the two given triangles, Δ ABC and ΔXYZ are congruent by the ASA rule.
Under ASA criterion, Δ ABC ≅ ΔXYZ, as ∠B = ∠Y, ∠C = ∠Z, and the side BC = YZ. Since Δ ABC ≅ ΔXYZ, then the third angle ∠A and the other two sides of Δ ABC are bound to be equal to the corresponding angle ∠X and the sides of ΔXYZ.
Angle Side Angle Congruence Rule Proof
Consider the two triangles, ABC and DEF in which ∠ B = ∠ E, ∠ C = ∠ F, and BC = EF
To Prove: Δ ABC ≅ Δ DEF.
For proving the congruence of the two triangles three cases arise.
Case 1: AB = DE (Assumed), ∠ B = ∠ E (Given), BC = EF (Given). Thus, Δ ABC ≅ Δ DEF (by SAS)
Case 2: Let if possible AB > DE and thus, we can take a point P on AB such that PB = DE. Now consider Δ PBC ≅ Δ DEF.
In Δ PBC and Δ DEF, PB = DE (By construction), ∠ B = ∠ E (Given), BC = EF (Given).
Thus, Δ PBC ≅ Δ DEF, by the SAS congruence rule.
Since the triangles are congruent, their corresponding parts will be equal. Thus, ∠ PCB = ∠ DFE. But, we are given that ∠ ACB = ∠ DFE. So, ∠ ACB = ∠ PCB. This is possible only if P coincides with A. or, BA = ED So, Δ ABC ≅ Δ DEF (by SAS axiom)
Angle Angle Side
Angle Angle Side or AAS postulate refers to two angles and one side of two triangles to prove its congruency. The AAS is one of the 5 congruency theorems that states that if two angles along with a non-included side are equal to the corresponding angles and non-included side of another triangle, the two triangles are considered to be congruent. The 5 congruence rules include SSS, SAS, ASA, AAS, and RHS. Let us learn more about the angle angle side theorem and solve a few examples.
| 1. | Angle Angle Side Definition |
| 2. | AAS Criterion for Congruence |
| 3. | Angle Angle Side Congruence Theorem |
| 4. | Proof of AAS Congruence Theorem |
| 5. | FAQs on Angle Angle Side |
Angle Angle Side Definition
By definition, angle angle side is a congruence theorem where it involves two angles and a non-included side. Hence, the theorem states that if any two angles and the non-included side of one triangle are equal to the corresponding angles and the non-included side of the other triangle. The angles are consecutive in nature and the sides are not included between the angles but in either direction of the angles. Look at the image below, we can see the two consecutive or next to each other angles of one triangle are equal to corresponding angles of another triangle. The sides of both the triangles are not included between the angles but are consecutive to the angles, hence the sides are also equal.
AAS Criterion for Congruence
AAS Criterion stands for Angle-Angle-Side Criterion. Under the AAS criterion, two triangles are congruent if any two angles and the non-included side of one triangle are equal to the corresponding angles and the non-included side of the other triangle.
If Δ ABC ≅ ΔXYZ under AAS criterion, then the third angle (∠ABC) and the other two sides (AC and BC) of Δ ABC is bound to be equal to the corresponding angle (∠XYZ) and the sides (XZ and YZ) of ΔXYZ.
Angle Angle Side Congruence Theorem
Angle-Angle-Side congruence theorem states that if two angles of a triangle with a non-included side are equal to the corresponding angles and non-included side of the other triangle, they are considered to be congruent. Let us see the proof of the theorem:
Given: AB = DE, ∠B=∠E, and ∠C =∠F. To prove: ∆ABC ≅ ∆DEF
If both the triangles are superimposed on each other, we see that ∠B =∠E and ∠C =∠F. And the non-included sides AB and DE are equal in length. Therefore, we can say that ∆ABC ≅ ∆DEF.
Proof of AAS Congruence Theorem
To prove the AAS congruence theorem, we need to first look at the ASA congruence theorem which states that when two angles and the included side (the side between the two angles) of one triangle are (correspondingly) equal to two angles and the included side of another triangle.
The AAS congruence theorem states that if any two consecutive angles of a triangle along with a non-included side are equal to the corresponding consecutive angles and the non-included side of another triangle, the two triangles are said to be congruent. We should also remember that if two angles of a triangle are equal to two angles of another, then their third angles are automatically equal since the sum of angles in any triangle must be a constant 180° (by the angle sum property).
To prove the AAS congruence rule, let us consider the two triangles above ∆ABC and ∆DEF. We know that AB = DE, ∠B =∠E, and ∠C =∠F. We also saw if two angles of two triangles are equal then the third angle of both the triangle is equal since the sum of angles is a constant of 180°. Hence,
From (i) and (ii) we get,
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
Since we already know that ∠B =∠E and ∠C =∠F, so
∠A + ∠E + ∠F = ∠D + ∠E + ∠F
In both the triangles we know that,
AB = DE, ∠A = ∠D, and ∠C =∠F
Therefore, according to the ASA congruence rule, it is proved that ∆ABC ≅ ∆DEF.
Examples on Angle Angle Side
Example 1: From the below image, which triangle follows the AAS congruence rule?
Solution:
From the above-given pairs, we can see that pair number 4 fits the AAS congruence rule where two consecutive angles with a non-included angle of one triangle are equal to the corresponding consecutive angles with a non-included side of another triangle, then the triangles are considered to be congruent. The pairs are of the other congruence rules such as,
Pair 1 = SSS Congruency Rule
Pair 2 = SAS Congruency Rule
Pair 3 = ASA Congruency Rule
Example 2: From the below triangle, we know that ∠Q = ∠R along with right angles on both sides of the triangle. Can we prove that ∆PQS ≅ ∆PRS?
Solution: Given,
∠Q = ∠R and ∠PSQ = ∠PSR = 90°
Since both the triangles share the same perpendicular line making the length of the line the same for both triangles. Hence, the sides of both triangles are also equal. According to the AAS congruence rule, we can say that ∆PQS ≅ ∆PRS.
Side Angle Side Formula
The side angle side formula which is also known as the SAS formula is used to calculate the area of the triangle using trigonometry rules. This formula which is based on the side angle side theorem helps us to calculate the area of a triangle. As the name suggests, side angle side represents the two sides and the angle between them. Let us explore more about the side angle side formula to calculate the area of a triangle.
What is Side Angle Side Formula?
The side angle side formula is the SAS area formula which means we can find the area of a triangle if the length of two sides of a triangle and its included angle is known. The SAS formula is expressed as:
Area of a triangle = (1/2) × side1 × side2 × sin (included angle)
The side angle side formula was created on the basis of the Side Angle Side Theorem. According to the Side Angle Side theorem, two triangles are said to be congruent if two sides and the angle that lies between these two sides are equal. The angle between the two sides is known as the included angle.
Derivation of Side Angle Side Formula
We know that the area of a triangle is = 1/2 × base × height. So, let us consider the following triangle to understand the derivation of the SAS formula using the steps given below.
Therefore, the side angle side formula or the area of the triangle using the SAS formula = 1/2 × a × b × sin c
Let us work on some problems to understand the side angle side formula.
Examples Using Side Angle Side Formula
Example 1: What will be the area of a triangle whose sides are of length 5 cm and 10 cm and its included angle is 30°?
Solution:
We know that the side angle side formula is given as:
Area of a triangle = (1/2) × side1 × side2 × sin (included angle)
Given: side1 = 5 cm, side2 = 10 cm, sin (included angle) = sin 30° = 1/2
Substituting the values,
Area = (1/2) × 5 × 10 × sin 30°
Answer: Thus, the area of the triangle is 12.5 cm 2
Example 2: In the triangle shown below, find all the dimensions using the side angle side formula.
Solution:
Given: Angle A = 49°, b = 5, c = 7
To find: a, Angle B, Angle C
Let us name side AB as c, and side AC as b
Let us follow the steps of the side angle side formula:
Step 1: To find the value of ‘a’ let us use the Law of Cosines
a 2 = b 2 + c 2 − 2bc cosA
a 2 = 5 2 + 7 2 − 2 × 5 × 7 × cos(49°)
a 2 = 25 + 49 − 70 × cos(49°)
a 2 = 74 − 70 × 0.6560.
a 2 = 74 − 45.924. = 28.075.
a = 5.30 (rounded upto 2 decimal places)
Step 2: To find the value of the smaller angle, we will use the law of sines
Angle B is smaller than Angle C as Angle B is opposite to the shorter side.
Thus, we will choose angle B and apply law of sines,
sin B / b = sin A / a
sin B / 5 = sin(49°) / 5.298.
sin B = (sin(49°) × 5) / 5.298.
B = 45.4° (rounded upto 1 decimal place)
Step 3: Now to find angle C, the angle sum property of the triangle can be used
C = 180° − 49° − 45.4°
C = 85.6°
Answer: Thus, we have calculated all the missing dimensions of the triangle.
FAQS on Side Angle Side Formula
What is the Side Angle Side Formula?
The side angle side formula which is also known as the SAS formula is used to calculate the area of the triangle using trigonometry rules. The formula is written as, Area of a triangle = (1/2) × side1 × side2 × sin (included angle), which means that if the two sides and the angle included between them is given then the area of the triangle can be calculated using the given formula.
What is the SAS Theorem in Geometry?
According to the Side Angle Side theorem, two triangles are said to be congruent if two sides and the angle that lies between these two sides are equal. The angle between the two sides is known as the included angle.
What is the Use of the Side Angle Side Formula?
The side angle side formula can be used to find the area of a triangle when the two sides and the included angle is given. The other uses of the formula are that we can find the hypotenuse, the unknown side of a right-angled triangle using the trigonometric law of Cosine. We can use the law of sines to find the smaller angle, and then the third angle of the triangle can be calculated since two angles are known.