What is variable in statistics
What is variable in statistics
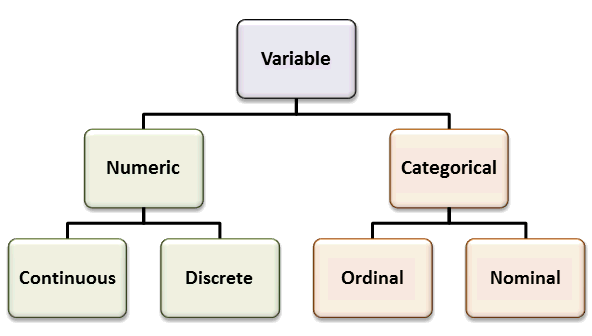
Variables in Statistics
A variable is any characteristics, number, or quantity that can be measured or counted. A variable may also be called a data item.
It is called a variable because the value may vary between data units in a population, and may change in value over time. For example; ‘income’ is a variable that can vary between data units in a population and can also vary over time for each data unit.
Types of Variables:
Numeric variables:
These variable have values that describe a measurable quantity as a number, like ‘how many’ or ‘how much’. Therefore numeric variables are quantitative variables. The data collected for a numeric variable are quantitative data. They may be further described as either continuous or discrete
Continuous Variable:
A continuous variable is a numeric variable which can take any value between a certain set of real numbers. The value given to an observation for a continuous variable can include values as small as the instrument of measurement allows. Their values are obtained by measuring. They are represented by connected points on graph. They can assumes infinite number of different values in the range.
Examples of continuous variables include height, time, age, and temperature.
Descrete Varaiable:
A discrete variable is a numeric variable which can take a value based on a count from a set of distinct whole values. They can assume a finite number of isolated values.
A discrete variable cannot take the value of a fraction between one value and the next closest value. Values are obtained by counting. They are represented by isolated points on the graph. They can whole number values in given range.
Examples: the number of registered cars, the number of children in a family, etc.
Catelogical Variable:
Categorical or qualitative variables can take values that describe a ‘quality’ or ‘characteristic’ of a data unit, like ‘what type’ or ‘which category’. Categorical variables fall into mutually exclusive (in one category or in another) and exhaustive (include all possible options) categories. They tend to be represented by a non-numeric value. The data collected for a categorical variable are qualitative data. They may be further described as either ordinal or nominal:
Ordinal Variable:
An ordinal variable is a categorical variable which can take a value that can be logically ordered or ranked. There is a clear ordering of the variables. The categories associated with ordinal variables can be ranked higher or lower than another, but do not necessarily establish a numeric difference between each category.
Examples of ordinal categorical variables include academic grades (i.e. A, B, C), clothing size (i.e. small, medium, large, extra large) and attitudes (i.e. strongly agree, agree, disagree, strongly disagree). If these categories were equally spaced, then the variable would be an interval variable.
Nominal Variable:
A nominal variable is a categorical variable which can take a value that is not able to be organised in a logical sequence.
Types of Measurement Scales from Type of variables:
Data can be classified as being on one of four scales: nominal, ordinal, interval or ratio. Each level of measurement has some important properties that are useful to know. For example, only the ratio scale has meaningful zeros.
Nominal:
The nominal scale places non-numerical data into categories or classifications. They are assigned a category. They don’t have a numeric value and so cannot be added, subtracted, divided or multiplied. They also have no order.
Ordinal:
The ordinal scale contains things that you can place in order. Ordinal scales are made up of ordinal data. For example, hottest to coldest, lightest to heaviest, richest to poorest, etc. Thus in ordinal scale the data is ranked.
The ordinal scale and interval scales are very similar to each other and are often confused. If you assume that the differences between the variables are equal the scale is an interval scale.
A major disadvantage with using the ordinal scale over other scales is that the distance between measurements is not always equal. If you have a list of numbers like 1, 2 and 3, you know that the distance between the numbers, in this case, is exactly 1. But if you had “very satisfied”, “satisfied” and “neutral”, there’s nothing to say if the difference between the three ordinal variables is equal.
Interval:
An interval scale has ordered numbers with meaningful divisions. It is a quantitative data with an ordered scale in which the interval between data values is meaningful. Zero is not meaningful in interval scale.
For example, the difference between a 100 O C and 90 O C is the same difference as between 70 O C and 80 O C.
Ratio:
The ratio scale is exactly the same as the interval scale with one major difference: zero is meaningful. For example, a temperature of 0 O C is meaningful. The zero in a ratio scale means that something doesn’t exist.
Example: Weight in kilograms is a very good example since it has a definite ratio from one weight to another. 50kg is indeed twice as heavy as 25 kg.
Note: If the clock starts ticking when you are born, but an age of “0” technically means you don’t exist. If the weighing scale shows 0 kg, therefore you don’t exist. If the height is 0 then have no height and hence do not exist.
Variables and Statistics
In statistics, variables are central to any analysis and they need to be understood well by the researcher. Even though the concept looks deceptively simple, many studies and experienced researchers can go wrong by using the wrong variables.
This article is a part of the guide:
Browse Full Outline
Like any variable in mathematics, variables can vary, unlike mathematical constants like pi or e. In statistics, variables contain a value or description of what is being studied in the sample or population.
For example, if a researcher aims to find the average height of a tribe in Columbia, the variable would simply be the height of the person in the sample. This is a simple measure for a simple statistical study. However, most statistical analyses are not as straightforward.
In many cases, statistical variables do not contain numerical values but rather something descriptive, such as the color of fins of a fish or the kind of species in a given natural habitat.
Qualitative to Quantitative Conversion
In many studies, the qualitative aspects of study are converted into numerical data for statistical analysis. In this case, the final variable used in the statistical analysis is a number instead of an attribute. This is central to good design of experiments.
For example, a research study might aim to find out how happy the sample group of students is before and after eating a bar of chocolate. In this case, it is very difficult to describe happiness, which is a very subjective and qualitative attribute. Converting this into a numerical scale of say 1-10 is what will give the study some credibility and help the researchers draw the right conclusions and inferences.
Quantitative Variables: Discrete and Continuous
Quantitative variables in statistics can be of different types, but the most commonly used classification is that they can either be discrete or continuous. These types of variables have some inherent differences that the researcher needs to be aware of.
For example, the test scores of a sample of students is clearly a discrete type of data that will be represented by discrete variables.
On the other hand, the signal noise produced in a study involving communicating devices is continuous in nature because the noise can take any value. This would be represented by a continuous variable.
Discrete to Continuous Conversion
These different types of variables require different kinds of analysis. For example, a number of continuous variables can be described using normal distribution. In fact, many discrete variables can also be represented in this manner when the sample space is so large that it looks like a continuous variable.
For example, the results of a coin toss involving 5 tosses is very discrete but if the number of flips is increased to 5000, the data looks smooth and continuous and the probability of obtaining say at least 2300 heads can be computed with a very good level of accuracy using continuous variables (coin tosses follow a normal distribution).
Types of Variables in Research & Statistics | Examples
Published on November 21, 2019 by Rebecca Bevans. Revised on July 21, 2022.
In statistical research, a variable is defined as an attribute of an object of study. Choosing which variables to measure is central to good experimental design.
Example
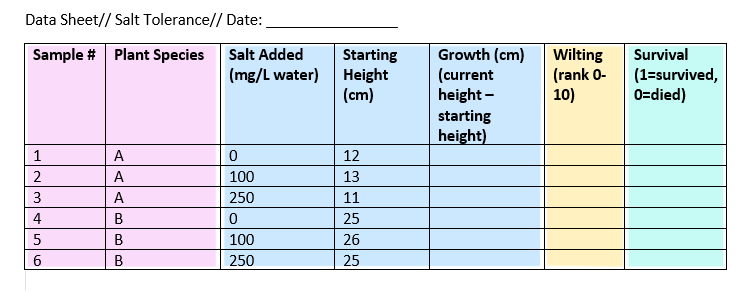
If you want to test whether some plant species are more salt-tolerant than others, some key variables you might measure include the amount of salt you add to the water, the species of plants being studied, and variables related to plant health like growth and wilting.
You need to know which types of variables you are working with in order to choose appropriate statistical tests and interpret the results of your study.
You can usually identify the type of variable by asking two questions:
Table of contents
Types of data: Quantitative vs categorical variables
Data is a specific measurement of a variable – it is the value you record in your data sheet. Data is generally divided into two categories:
A variable that contains quantitative data is a quantitative variable; a variable that contains categorical data is a categorical variable. Each of these types of variable can be broken down into further types.
Quantitative variables
When you collect quantitative data, the numbers you record represent real amounts that can be added, subtracted, divided, etc. There are two types of quantitative variables: discrete and continuous.
Categorical variables
Categorical variables represent groupings of some kind. They are sometimes recorded as numbers, but the numbers represent categories rather than actual amounts of things.
There are three types of categorical variables: binary, nominal, and ordinal variables.
*Note that sometimes a variable can work as more than one type! An ordinal variable can also be used as a quantitative variable if the scale is numeric and doesn’t need to be kept as discrete integers. For example, star ratings on product reviews are ordinal (1 to 5 stars), but the average star rating is quantitative.
Example data sheet
To keep track of your salt-tolerance experiment, you make a data sheet where you record information about the variables in the experiment, like salt addition and plant health.
Parts of the experiment: Independent vs dependent variables
Experiments are usually designed to find out what effect one variable has on another – in our example, the effect of salt addition on plant growth.
You manipulate the independent variable (the one you think might be the cause) and then measure the dependent variable (the one you think might be the effect) to find out what this effect might be.
You will probably also have variables that you hold constant (control variables) in order to focus on your experimental treatment.
| Type of variable | Definition | Example (salt tolerance experiment) |
|---|---|---|
| Independent variables (aka treatment variables) | Variables you manipulate in order to affect the outcome of an experiment. | The amount of salt added to each plant’s water. |
| Dependent variables (aka response variables) | Variables that represent the outcome of the experiment. | Any measurement of plant health and growth: in this case, plant height and wilting. |
| Control variables | Variables that are held constant throughout the experiment. | The temperature and light in the room the plants are kept in, and the volume of water given to each plant. |
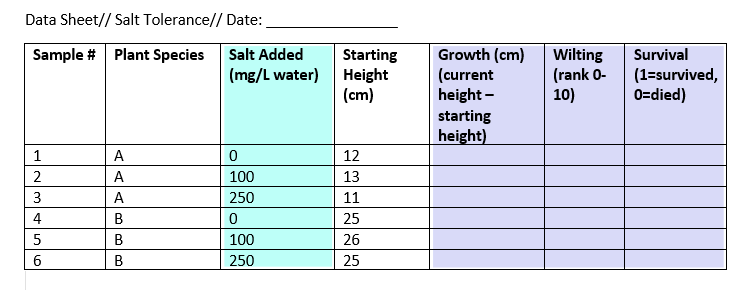
Example data sheet
In this experiment, we have one independent and three dependent variables.
The other variables in the sheet can’t be classified as independent or dependent, but they do contain data that you will need in order to interpret your dependent and independent variables.
What about correlational research?
Types of Variable
All experiments examine some kind of variable(s). A variable is not only something that we measure, but also something that we can manipulate and something we can control for. To understand the characteristics of variables and how we use them in research, this guide is divided into three main sections. First, we illustrate the role of dependent and independent variables. Second, we discuss the difference between experimental and non-experimental research. Finally, we explain how variables can be characterised as either categorical or continuous.
Dependent and Independent Variables
An independent variable, sometimes called an experimental or predictor variable, is a variable that is being manipulated in an experiment in order to observe the effect on a dependent variable, sometimes called an outcome variable.
Imagine that a tutor asks 100 students to complete a maths test. The tutor wants to know why some students perform better than others. Whilst the tutor does not know the answer to this, she thinks that it might be because of two reasons: (1) some students spend more time revising for their test; and (2) some students are naturally more intelligent than others. As such, the tutor decides to investigate the effect of revision time and intelligence on the test performance of the 100 students. The dependent and independent variables for the study are:
Dependent Variable: Test Mark (measured from 0 to 100)
Independent Variables: Revision time (measured in hours) Intelligence (measured using IQ score)
The dependent variable is simply that, a variable that is dependent on an independent variable(s). For example, in our case the test mark that a student achieves is dependent on revision time and intelligence. Whilst revision time and intelligence (the independent variables) may (or may not) cause a change in the test mark (the dependent variable), the reverse is implausible; in other words, whilst the number of hours a student spends revising and the higher a student’s IQ score may (or may not) change the test mark that a student achieves, a change in a student’s test mark has no bearing on whether a student revises more or is more intelligent (this simply doesn’t make sense).
In the section on experimental and non-experimental research that follows, we find out a little more about the nature of independent and dependent variables.
Experimental and Non-Experimental Research
Categorical and Continuous Variables
Categorical variables are also known as discrete or qualitative variables. Categorical variables can be further categorized as either nominal, ordinal or dichotomous.
Continuous variables are also known as quantitative variables. Continuous variables can be further categorized as either interval or ratio variables.
Ambiguities in classifying a type of variable
It is worth noting that how we categorise variables is somewhat of a choice. Whilst we categorised gender as a dichotomous variable (you are either male or female), social scientists may disagree with this, arguing that gender is a more complex variable involving more than two distinctions, but also including measurement levels like genderqueer, intersex and transgender. At the same time, some researchers would argue that a Likert scale, even with seven values, should never be treated as a continuous variable.
Stats and R
Introduction
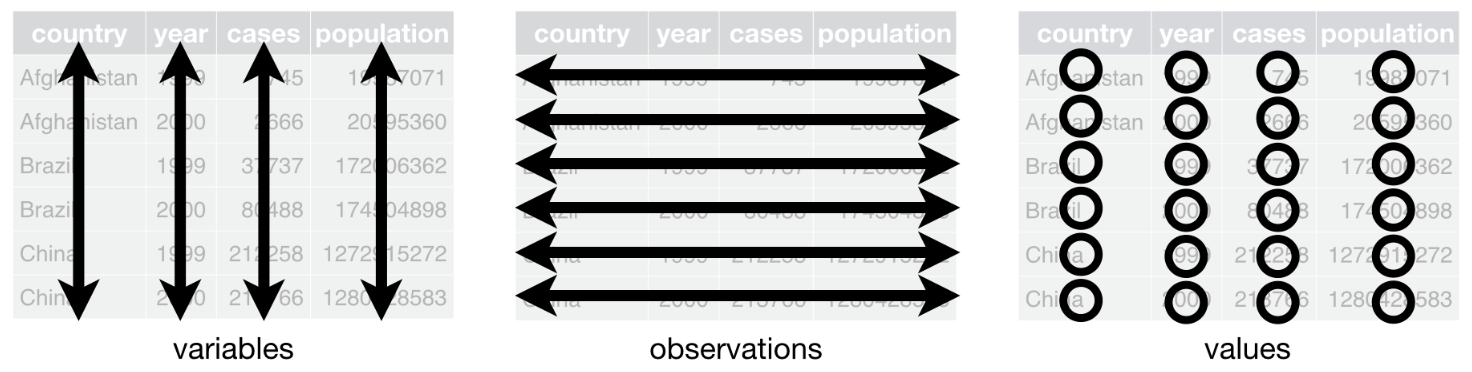
If you happen to work with datasets frequently, you probably know that each row of your dataset represents a different experimental unit (also called observation) and each column represents a different characteristic (called variable):
Structure of a dataset. Source: R for Data Science by Hadley Wickham & Garrett Grolemund
If you do some research on the weight and height of 100 students of your university, for example, you will most likely have a dataset containing 100 rows and three columns:
These three columns represent three characteristics of the 100 students. They are called variables.
In this article, we are going to focus on variables, and in particular to the different types of variable that exist in statistics. (To learn about the different data types in R, read “Data types in R”.)
Different types of variables for different types of statistical analysis
First, one may wonder why we are interested in defining the types of our variables of interest.
The reason why we often class variables into different types is because not all statistical analyses can be performed on all variable types. For instance, it is impossible to compute the mean of the variable “hair color” as you cannot sum brown and blond hair.
On the other hand, finding the mode of a continuous variable does not really make any sense because most of the time there will not be two exact same values, so there will be no mode. And even in the case there is a mode, there will be very few observations with this value. As an example, try finding the mode of the height of the students in your class. If you are lucky, a couple of students will have the same size. However, most of the time, every student will have a different size (especially if heights have been measured in millimeters) and thus there will be no mode. To see what kind of analysis is possible on each type of variable, see more details in the articles “Descriptive statistics by hand” and “Descriptive statistics in R”.
Similarly, some statistical tests can only be performed on certain type of variables. For example, the Pearson correlation is usually computed on quantitative variables, while a Chi-square test of independence is done with qualitative variables, and a Student t-test or ANOVA requires a mix of quantitative and qualitative variables.
Big picture
In statistics, variables are classified into 4 different types:
Quantitative
A quantitative variable is a variable that reflects a notion of magnitude, that is, if the values it can take are numbers. A quantitative variable represents thus a measure and is numerical.
Quantitative variables are divided into two types: discrete and continuous. The difference is explained in the following two sections.
Discrete
Quantitative discrete variables are variables for which the values it can take are countable and have a finite number of possibilities. The values are often (but not always) integers. Here are some examples of discrete variables:
Even if it would take a long time to count the citizens of a large country, it is still technically doable. Moreover, for all examples, the number of possibilities is finite. Whatever the number of children in a family, it will never be 3.58 or 7.912 so the number of possibilities is a finite number and thus countable.
Continuous
On the other hand, quantitative continuous variables are variables for which the values are not countable and have an infinite number of possibilities. For example:
For simplicity, we usually referred to years, kilograms (or pounds) and centimeters (or feet and inches) for age, weight and height respectively. However, a 28-year-old man could actually be 28 years, 7 months, 16 days, 3 hours, 4 minutes, 5 seconds, 31 milliseconds, 9 nanoseconds old.
For all measurements, we usually stop at a standard level of granularity, but nothing (except our measurement tools) prevents us from going deeper, leading to an infinite number of potential values. The fact that the values can take an infinite number of possibilities makes it uncountable.
Qualitative
In opposition to quantitative variables, qualitative variables (also referred as categorical variables or factors in R) are variables that are not numerical and which values fits into categories.
In other words, a qualitative variable is a variable which takes as its values modalities, categories or even levels, in contrast to quantitative variables which measure a quantity on each individual.
Qualitative variables are divided into two types: nominal and ordinal.
Nominal
A qualitative nominal variable is a qualitative variable where no ordering is possible or implied in the levels.
For example, the variable gender is nominal because there is no order in the levels (no matter how many levels you consider for the gender—only two with female/male, or more than two with female/male/others, levels are unordered). Eye color is another example of a nominal variable because there is no order among blue, brown or green eyes.
A nominal variable can have:
Note that a qualitative variable with exactly 2 levels is also referred as a binary or dichotomous variable.
Ordinal
On the other hand, a qualitative ordinal variable is a qualitative variable with an order implied in the levels. For instance, if the severity of road accidents has been measured on a scale such as light, moderate and fatal accidents, this variable is a qualitative ordinal variable because there is a clear order in the levels.
Another good example is health, which can take values such as poor, reasonable, good, or excellent. Again, there is clear order in these levels so health is in this case a qualitative ordinal variable.
Variable transformations
There are two main variable transformations:
From continuous to discrete
Let’s say we are interested in babies’ ages. The data collected is the age of the babies, so a quantitative continuous variable. However, we may work with only the number of weeks since birth and thus transforming the age into a discrete variable. The variable age remains a quantitative continuous variable but the variable we are working on (i.e., the number of weeks since birth) is a quantitative discrete variable.
From quantitative to qualitative
Let’s say we are interested in the Body Mass Index (BMI). For this, a researcher collects data on height and weight of individuals and computes the BMI. The BMI is a quantitative continuous variable but the researcher may want to turn it into a qualitative variable by categorizing individuals below a certain threshold as underweighted, above a certain threshold as overweighted and the rest as normal weight. The raw BMI is a quantitative continuous variable but the categorization of the BMI makes the transformed variable a qualitative (ordinal) variable, where the levels are in this case underweighted 2000€).
Additional notes
Misleading data encoding
Last but not least, in datasets it is very often the case that numbers are used for qualitative variables. For instance, a researcher may assign the number “1” to women and the number “2” to men (or “0” to the answer “No” and “1” to the answer “Yes”). Despite the numerical classification, the variable gender is still a qualitative variable and not a discrete variable as it may look. The numerical classification is only used to facilitate data collection and data management. It is indeed easier to write the number “1” or “2” instead of “women” or “men”, and thus less prone to encoding errors.
The same goes for the identification of each observation. Suppose you collected information on 100 students. You may use their student’s ID to identify them in the dataset (so that you can trace them back). Most of the time, students’ ID (or ID in general) are encoded as numeric values. At first sight, it may thus look like a quantitative variable. However, ID is clearly not a quantitative variable because it actually corresponds to an anonymized version of the student’s first and last name. If you think about it, it would make no sense to compute the mean or median on the IDs, as it does represent a measurement (but rather just an easy way to identify students).
If you face this kind of setup, do not forget to transform your variable into the right type before performing any statistical analyses. Usually, a basic descriptive analysis (and knowledge about the variables which have been measured) prior to the main statistical analyses is enough to check that all variable types are correct.
Thanks for reading. I hope this article helped you to understand the different types of variable. If you would like to learn more about the different data types in R, read the article “Data types in R”.
As always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.