What number base could you use as a shorthand for base 2 binary
What number base could you use as a shorthand for base 2 binary
Number Bases
Humans count in base 10, but there are other ways to represent numbers.
Decimal / Base 10 / Denary
This is the number base we’re used to. We use the numbers 0 to 9 to represent numbers.
It’s thought that humans use decimal because we have ten fingers.
Decimal is notated with a subscript 10, like this: 2310
Binary / Base 2
Computers use binary as it can be represented with a high or low current. Only the values 1 and 0 are used.
Binary is notated with a subscript 2, like this: 100110110102
Binary numbers can be converted to decimal using column headers which double in value, starting from 1.
Hexadecimal / Base 16
Hexadecimal uses the numbers 0 to 9 and the letters A to F. A is the equivalent of 10 in decimal and F is 15.
Hexadecimal is good to use when memory is at a premium. A large range of numbers can be represented with very few characters. It’s also easy to covert to and from binary so is often used as «shorthand» for base 2 as it requires fewer characters.
Hexadecimal numbers are notated with a subscript 16, like this: 4E16
The least significant part of a hexadecimal number is furthest to the right and is worth just its value.
(16 * 10) + (1 * 1) = 161
To convert from hexadecimal to binary, convert each digit into a binary nibble (4 bits) like in the picture below.
1101 is 13 in decimal.
13 = D in hexadecimal.
TryHackMe: Introductory Researching
[Task 1] Introduction
[Task 2] Example Research Question
3. What are automated tasks called in Linux?
ANS: Cron ****
[Task 3] Vulnerability Searching
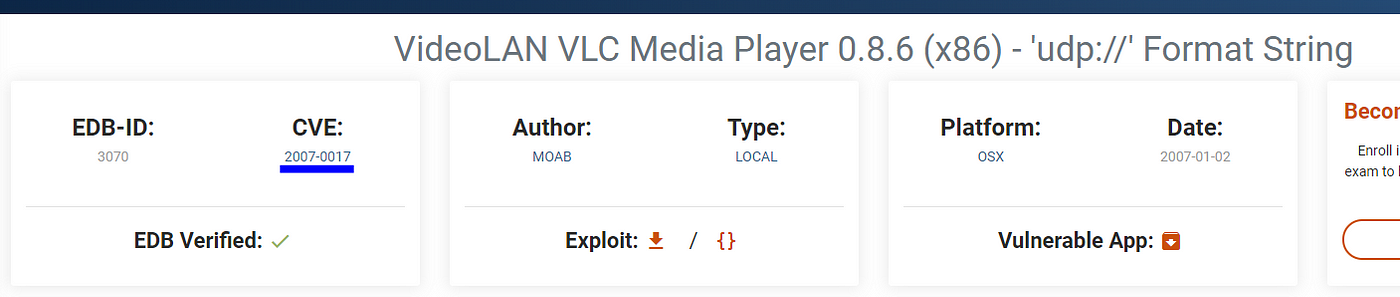
I will use exploit-db
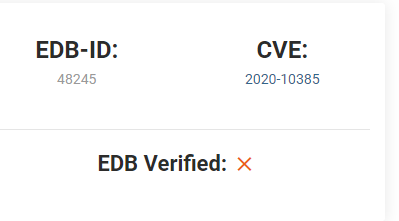
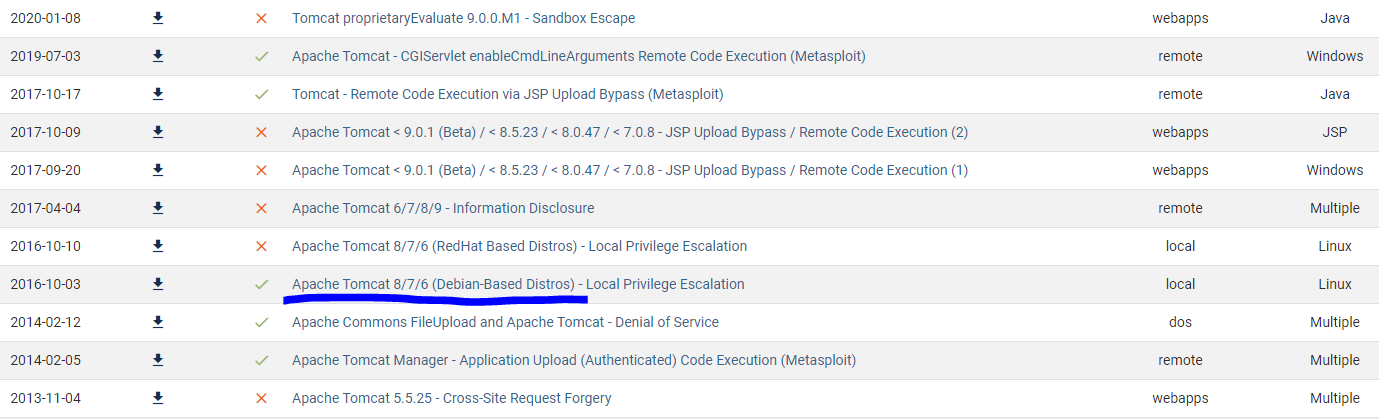
2. There was a Local Privilege Escalation vulnerability found in the Debian version of Apache Tomcat, back in 2016. What’s the CVE for this vulnerability?
3. What is the very first CVE found in the VLC media player?
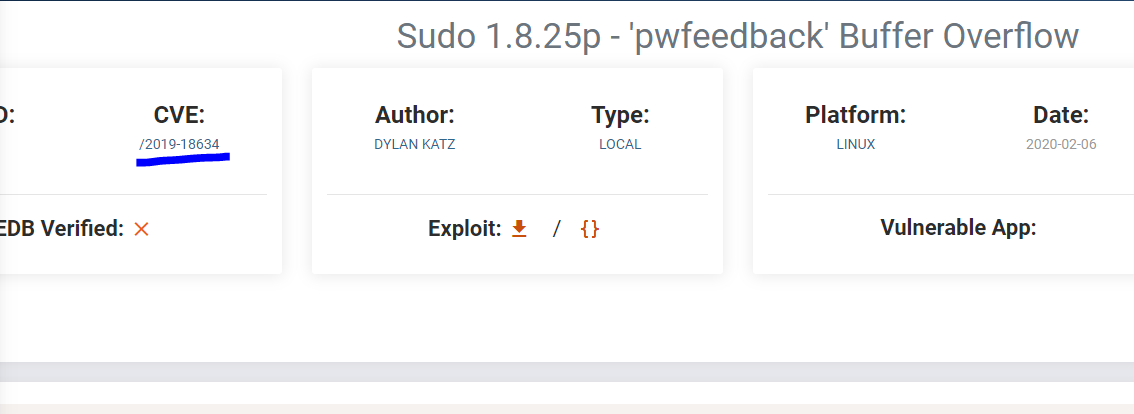
4. If I wanted to exploit a 2020 buffer overflow in the sudo program, which CVE would I use?
[Task 4] Manual Pages
2. fdisk is a command used to view and alter the partitioning scheme used on your hard drive.
What switch would you use to list the current partitions?
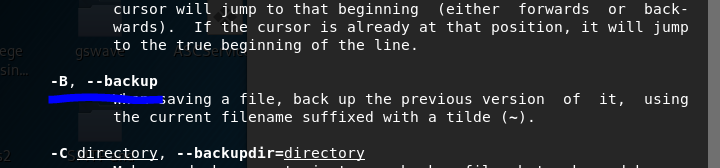
3. nano is an easy-to-use text editor for Linux. There are arguably better editors (Vim, being the obvious choice); however, nano is a great one to start with.
What switch would you use to make a backup when opening a file with nano?
4. Netcat is a basic tool used to manually send and receive network requests.
What command would you use to start netcat in listen mode, using port 12345?
Binary & Hexidecimal Numbering Systems
It is time to abandon your reliance on the base 10 numbering system. It is after all a human construct that probably is based on the number of fingers most people have. Mathematics is perfectly happy with numbering systems based on different numbers of digits. In electrical engineering and computer science, we take advantage of this fact and use the binary numbering system to represent logic states. The binary numbering system is base 2 and just uses the digits 0 and 1.
Binary is base 2 and uses just 0 and 1
We also use hexidecimal, which is base 16, but this is really just used as shorthand for binary as you will see. With hexidecimal we need 16 digits, and these are represented by 0-9 followed by A-F.
Hexideciaml is base 16 and uses 0-9 and A-F
Decimal Numbering System (Base 10)
In order to understand different numbering systems and how to convert from one to another, we need to break down and understand our native base 10 system. Base 10 numbering system means that each position in a number can be one of ten different digits. It also means that the total value of a number in base 10 is the sum of the digits in each position multiplied by powers of 10 in ascending order from right to left starting with power of 0. Below is the number two-thousand, six hundred and fourteen with powers of ten positions identified.
| 2 | 6 | 1 | 4 |
| 10 3 | 10 2 | 10 1 | 10 0 |
Binary Numbering System (Base 2)
The binary numbering system is base 2, and each position in a binary number represents the amount of a power of 2 starting with power of 0 and ascending from right to leftt. It is like base 10, except change powers of 10 to powers of 2, and there are 2 possible values in each number position instead of 10. Here is an example number:
| 1 | 0 | 1 | 0 |
| 2 3 | 2 2 | 2 1 | 2 0 |
In order to convert this number to decimal (base 10) perform the powers of 2 multiplications in base 10 for each position, multiply that by the value in that position, and sum it up. The number above would be 1*8 + 0*4 + 1*2 + 0*1 = 10 in decimal.
When writing a binary number, we often add a lower case b to the end of the number to make it clear that it is a binary number and not decimal, because 1010 is also a valid decimal number. So, we would write 1010b to be clear.
Hexidecimal Numbering System (Base 16)
The hexidecimal numbering system is base 16, and each postion in a hex number has 16 possible values. There are only ten numeric characters in the English language, 0-9, so in addition we use A-F to represent values 10-15.
| A | 7 | E | 4 |
| 16 3 | 16 2 | 16 1 | 16 0 |
This hexidecimal number can be converted to decimal by following the same process used for binary number conversion, except ou need to replace the alpha characters with their numeric values. 10*4096 + 7*256 + 14*16 + 4*1 = 42980 in decimal. You can see that hexidecimal can represent alot of values with just a few digits. We denote a hexidecimal number with a lower case h at the end or more commonly with a 0x at the beginning. So, we would write A7E4h or 0xA7E4 to be clear.
Binary is the numbering system we need to represent the two logic states: false represented by 0, and true represented by 1. Hexidecimal is used extensively as a shorthand for binary. Because it is base 16 with 16 being a power of 2, conversion from binary to hex is clean. All the possible values in a 4 digit binary number can be represented by a 1 digit hex number using all its possible values. A 4 digit binary number can represent values 0-15 (decimal), and a 1 digit hex number can represent values 0-15 (decimal).
To convert from binary to hex, so can use the same process as above, but the numbers being multiplied and added need to be hex numbers. For example, 10010b = 1*2 4 + 0*2 3 + 0*2 2 + 1*2 1 + 0*2 0 = 1*10 + 0*8 + 0*4 + 1*2 + 0*1 = 0x12. Note that each number is in hex, and the first term, 1*10, would be 1*16 in decimal. In pactice, I think most folks convert from binary to decimal and then from decimal to hex. Something like: 10010b has a 16 plus a 2 which is 18. That’s more than 16 and less than 32, so the second position has a 1 which is 16 leaving 2, so 0x12 is the answer.
Why Base 2 with binary numbers?
History: I read from one of Knuth’s algorithm book that first computers used the base of 10. Then, it switched to two’s complement here.
Examples:
8 Answers 8
Trending sort
Trending sort is based off of the default sorting method — by highest score — but it boosts votes that have happened recently, helping to surface more up-to-date answers.
It falls back to sorting by highest score if no posts are trending.
Switch to Trending sort
At its heart, digital logic is base two. A digital signal is either on or off. Supporting other bases (as in BCD) means wasted representation space, more engineering, more complex specification, etc.
Editted to add: In addition to the trivial representation of a single binary digit in digital logic, addition is easily realized in hardware, start half adder which is easily realized in Boolean logic (i.e. with transistors):
Which brings us to twos complement: negation is easy, and the addition of mixed positive and negative number follows naturally with no additional hardware. So subtraction comes almost for free.
Few other representations will allow arithmetic to be implemented so cheaply, and I know of none that are easier.
Optimization in storage and optimization in processing time are often at cross purposes with each other; all other things being equal, simplicity usually trumps complexity.
Anyone can propose any storage mechanism for information they wish, but unless there are processors or algorithms that support it, it won’t get used.
Second, 2s complement hardware is simple to implement. Not only is simple to implement, it is super simple to implement 2s complement hardware that supports both signed and unsigned arithmetic, since they are the same thing. In other words, the binary representation of uint4(8) and sint4(-15) are the same, and the binary representation of uint(7) and sint4(7) are the same, which means you can do the addition without knowing whether or not it is signed, the values all work out either way. That means the HW can totally avoid knowing anything about signs and let it be dealt with as a language convention.
In the end the decision was made because of voltage variance.
With base 2 it is on or off, no in between.
However with base 10 how do you know what each number is?
A shorthand for base 2 (binary)
I was doing TryHackMe and I encountered this question. I got this answer by looking through some help from the TryHackMe forum but I could not find an explanation to why 16 is the shorthand for base 2? Can someone explain to me why 16 is the correct answer in this case but not Base 8? Thank you for your help
3 Answers 3
Trending sort
Trending sort is based off of the default sorting method — by highest score — but it boosts votes that have happened recently, helping to surface more up-to-date answers.
It falls back to sorting by highest score if no posts are trending.
Switch to Trending sort
I got off on the wrong foot on this one.
So a binary number can be represented as 110011, for example (base 2). In reality, you would not use that. People use either octal or hex. So the question becomes: which one is the most common, and how would you name it?
The way they’ve phrased the question makes it look like any numbering system could be a possible answer.
Base 16 would be better because you can represent 4 binary digits using a single hexadecimal digit whereas one octal digit can represent 3 binary digits.
Therefore you can represent large number of values using fewer hexadecimal digits.