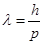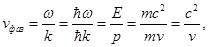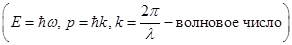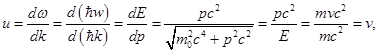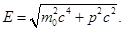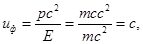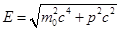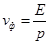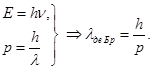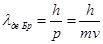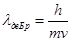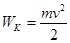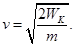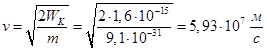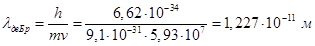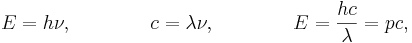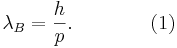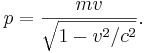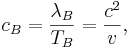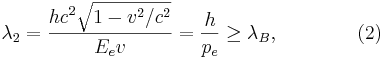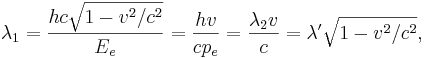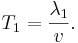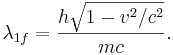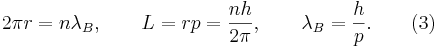длина волны де бройля в чем измеряется

Как определить длину волны де Бройля для электрона

Волна де Бройля или волна амплитуды вероятности

Волна де Бройля является волной вероятности или волной амплитуды вероятности, которая определяет плотность вероятности обнаружения объекта в конкретной точке конфигурационного пространства.

Согласно определения волн де Бройля, можно сделать вывод об их взаимодействии с какими-либо частицами и их волновой природе. Формулировка волн материи была введена в науку в 1924 году французским физиком-теоретиком Луи де Бройлем. Благодаря теории, свойство корпускулярно-волнового дуализма (или двойственности) было распространено на любые проявления материи, включая излучение и какие-либо частицы вещества.

В современной квантовой теории «волна материи» понимается несколько иначе. Однако название данного физического феномена, связанного с частицами вещества, включая водород, сформулировано в честь автора гипотезы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В 1913 году Н. Бор предложил полуклассическую модель атома, в основе которой было два постулата:

Таким образом, боровская модель атома не предусматривает излучение электрона на орбите, его нахождение между орбитами. Однако согласно простой рассматриваемой модели, движение электрона рассматривают с классической точки зрения, как вращение планеты вокруг Солнца.

В процессе поиска ответа на вопрос о поведении электрона Де Бройль предположил, что электрону в любом случае должна соответствовать определенная волна. Благодаря ей, частица «выбирает» исключительно такие орбиты, на которых данная волна укладывается целое число раз. В этом и заключался смысл целочисленного коэффициента в постулированной Бором формуле.

Гипотеза приводит к выводу, что электронная волна де Бройля не является электромагнитной, а волновые параметры должны быть характерны для любых материальных частиц, а не только для электронов в атоме. Ученому удалось получить важное соотношение, с помощью которого можно определить тип этих рассматриваемых волновых свойств. Формула расчета волны де Бройля:

где λ – является длиной волны, p – определяет импульс частицы в уравнении.

Природа волн де Бройля, фазовая и групповая скорость

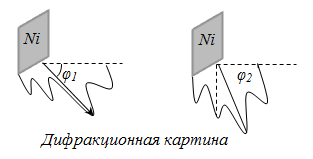
Следует отметить, что волны де Бройля, называемые электронными волнами, не являются электромагнитными. В 1927 году американским физикам Дэвиссону и Джермеру удалось подтвердить гипотезу де Бройля. Ученые обнаружили дифракцию электронов на кристалле никеля. В процессе получилось определить дифракционные максимумы, которые соответствуют формуле Вульфа-Брэггов:

Расчет брэгговской длины волны подтвердил ее соответствие формуле:

В дальнейшем гипотеза де Бройля была подтверждена опытным путем Л.С. Тартаковским и Г. Томсоном. Ученым удалось зафиксировать дифракционную картину, когда пучок быстрых электронов при Е≈ 50 кэВ проходит сквозь фольгу из разных металлов.

Чуть позже получилось обнаружить дифракцию нейтронов, протонов, атомных пучков и молекулярных пучков. В дальнейшем были изобретены инновационные методики исследования вещества, включая нейтронографию и электронографию, сформировалось направление электронной оптики.

Макротела должны характеризоваться аналогичными свойствами. В случае, если m = 1кг, \(l = 6,62*10^ <-31>м\) – невозможно обнаружить современными методами – поэтому макротела рассматриваются только в качестве корпускул.

В том случае, когда частица с массой m перемещается со скоростью v, фазовая скорость волн де Бройля будет определяться по формуле:

Исходя из того, что c > v, фазовая скорость волн де Бройля превышает скорость света в вакууме. Можно отметить, что фазовая скорость Vф может быть больше и может быть меньше с, в отличие от групповой скорости. Формула групповой скорости:

Таким образом, групповая скорость волн де Бройля соответствует скорости движения частицы. В случае фотона она будет равна:

В результате, значение групповой скорости равно скорости света.

Волны де Бройля подвержены дисперсии. Если подставить выражение:

получим следующее равенство:

Так как присутствует дисперсия, волны де Бройля невозможно представить, как волновой пакет. В противном случае, он мгновенно «расплывется», то есть исчезнет, в течение 10-26 с.

Какой формулой определяется длина волны

Количественные соотношения, которые связывают корпускулярные и волновые способности частиц, аналогичны свойствам фотонов:

Гипотеза де Бройля основана на универсальном характере данного равенства, что справедливо в условиях любых волновых процессов. Какой-либо частице, которая обладает импульсом р, соответствует волна. Ее длину можно определить с помощью формулы де Бройля:

p =mv— является импульсом частицы, h – определяется, как постоянная Планка.

Как определить длину волны де Бройля для электрона

Рассчитать длину волны де Бройля для электрона можно на конкретном примере. Предположим, то требуется определить длину волны де Бройля λ для электрона, кинетическая энергия которого составляет:

В первую очередь стоит записать исходные данные:

Формула волны де Бройля:

Так как известна кинетическая энергия электронов, можно рассчитать их скорость:

Далее можно определить длину волны де Бройля:

В том случае, когда скорость v частиц соизмерима со скоростью света с, длину волны де Бройля можно рассчитать по формуле:

Источник

Электронные волны де Бройля

«Де Бройль был первым, кто осознал тесную физическую и формальную взаимосвязь между квантовыми состояниями материи и явлениями резонанса еще в те времена, когда волновая природа материи не была открыта экспериментально.»
Альберт Эйнштейн

Если кванты света могут себя вести и как волна, и как частица, то могут ли подобным образом вести себя другие микрочастицы, составляющие атом? Настала пора ответить и на этот вопрос.

Мы уже знаем, что фотон ведет себя в пространстве не только как некий материальный объект — корпускула, но и как волна. Причем длина этой волны определяется формулой 1 = h/р, где h — постоянная Планка, а р — импульс частицы. Вопросом, любая ли движущаяся частица может себя вести подобным образом, заинтересовался французский физик-теоретик Луи де Бройль.

Частица превращается. В волну

Напомним, что впервые квантовые свойства были открыты Максом Планком при исследовании законов теплового излучения тел. Тогда в науку и вошло представление о «световых порциях» — квантах электромагнитного поля. Вместе с тем уже давно были известны волновые свойства электромагнитного излучения, проявляющиеся, например, в явлениях дифракции (огибании светом препятствий, сравнимых с длиной волны) и интерференции (наложении волн друг на друга) света.

Впервые идею о корпускулярно-волновой природе электрона французский физик выдвинул еще в 1923 году. Позднее это оказалось справедливым и для других составляющих атома. Выдвинутая им гипотеза хорошо обосновала казавшийся загадочным принцип стационарных орбит в модели атома Бора.

Де Бройль предположил, что если частица имеет массу m и скорость v, значительно меньшую скорости света с, импульс частицы р = mv, то длина волны должна определяться формулой А = h/mv.

Волновые свойства электронов должны проявиться, например, при их рассеянии на кристаллах, на которых уже к этому времени наблюдали дифракцию рентгеновских лучей.

Оставалось проверить теорию на практике. Как же это сделать?

Окошко в микромир

Впервые экспериментальное подтверждение гипотезы де Бройля осуществили американские ученые Клинт Дэвиссон и Лестер Джермер. Они разогнали пучок электронов в электрическом поле с разностью потенциалов до 150 вольт и пустили его на кристалл никеля. Было установлено, что на кристалле происходит дифракция электронов, причем полученная длина соответствует соотношению де Бройля, а следовательно, электрон в данном случае действительно ведет себя как волна.

Таким образом, подтвержденная на опыте идея де Бройля о корпускулярно-волновом дуализме микрочастиц принципиально изменила представления об облике микромира. Поскольку всем микрообъектам — по традиции будем все же называть их частицами — присущи и корпускулярные, и волновые свойства, то любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании этих слов. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу именно такой теории — волновой, или квантовой механики, и легла подтвержденная гипотеза де Бройля.

Сегодня волновые свойства составляющих атом частиц, а также самих атомов и молекул не только доказаны прямыми опытами, но и широко используются в установках с высокой разрешающей способностью.

Существование волн де Бройля лежит в основе работы электронного микроскопа, разрешающая способность которого на много порядков выше, чем у любого оптического микроскопа, что позволяет ученым наблюдать молекулы и атомы. Метод дифракции частиц в настоящее время широко используется при изучении строения и свойств вещества.

«Полезно поразмыслить над ошибками, сделанными великими умами, поскольку они часто имели серьезное основание, чтобы их сделать» (Луи де Бройль)

Источник

Волны де Бройля

Идея о волнах, связанных не только с квантами света, но и массивными частицами, предложена Луи де Бройлем в 1923–1924 годах и называется гипотезой де Бройля. Хотя трактовка квадрата модуля амплитуды волны как плотности вероятности в конфигурационном пространстве принадлежит Максу Борну, по традиции и в знак признания заслуг французского физика говорят о волнах де Бройля.

Идея волн де Бройля полезна для приблизительных выводов о масштабах проявления волновых свойств частиц, но не отражает всей физической реальности и потому не лежит в основе математического аппарата квантовой механики. Вместо дебройлевских волн эту роль в квантовой механике выполняет волновая функция, а в квантовой теории поля — полевые операторы.

Связанные понятия

Эта статья — об энергетическом спектре квантовой системы. О распределении частиц по энергиям в излучении см. Спектр, Спектр излучения. Об энергетическом спектре сигнала см. Спектральная плотность.Энергетический спектр — набор возможных энергетических уровней квантовой системы.

Основные положения статистической интерпретации волновой функции были сформулированы М. Борном в 1926 году, как только было опубликовано волновое уравнение Шрёдингера. В отличие от интерпретации Шрёдингера, представляющей электрон в атоме в виде волнового пакета, интерпретация М.Борна рассматривала электрон в атоме как отрицательно заряженную элементарную частицу и сохраняла структуру электрона. Но при этом законы движения электрона в атоме приобретают вероятностный характер, определяемый волновой.

В теории поля представление системы зарядов в виде некоторых квадрупо́лей, аналогично представлению её в виде системы диполей, используется для приближённого расчёта создаваемого ей поля и излучения. Более общим представлением является разложение системы на мультиполи, соответствующее разложению потенциалов в ряд Тейлора по некоторым переменным. Квадруполь — частный случай мультиполя. Квадрупольное рассмотрение системы оказывается особенно важным в том случае, когда её дипольный момент и заряд равны.

Пра́вилами отбо́ра в спектроскопии называют ограничения и запрет на переходы между уровнями квантомеханической системы с поглощением или излучением фотона, наложенные законами сохранения и симметрией.

Источник

«Волновые свойства микрочастиц. Волны де Бройля»

Разделы: Физика

Волновые свойства микрочастиц. Волны де Бройля.

Французский физик Луи де Бройль – потомок королей и будущий Нобелевский лауреат, родился в 1892 году.

Как и многие во время I Мировой войны воевал, а после войны стал работать в лаборатории своего старшего брата Мориса. Его занимал всё тот же вопрос: “Почему атомы устойчивы? Почему на стационарных орбитах электроны не излучают?”
Третий постулат Бора выделял эти орбиты из набора всех мыслимых орбит правилом квантования:

Де Бройль хотел найти разумные основания для этого условия, то есть пытался понять физический смысл правила квантования.

В 1923 году де Бройль выдвинул гипотезу: не только свет, но и все тела в природе должны обладать и волновыми, и корпускулярными свойствами одновременно.

Чтобы понять это, нужно иметь непредвзятый ум. Природа не создала зримых образов, которые помогли бы наглядно представить это.

Длина волны , присущая частицам вещества, получила название длины волны де Бройля, а сами такие волны – волны де Бройля.

Волны де Бройля для электрона.

Движение электрона вокруг ядра в атоме будет устойчивым тогда, когда на длине орбиты укладывается целое число n длин волн электрона.

, откуда . Домножим на h, имеем

, ;

Получили третий постулат Бора.

Рис. 1 Иллюстрация теории де Бройля

Новое понятие стационарной орбиты: это такая орбита, на которой укладывается целое число длин волн электрона.

Определим длину волны электрона.

; (*)

Выразим n из третьего постулата и подставим в (*). Получим:

;

Пример: электрон в атоме движется со средней скоростью v=10 6 м/с, тогда длина волны электрона в атоме .

Волны де Бройля для частиц вещества.

I. Если частица релятивистская .

Применение микрочастиц для исследования структуры вещества.

В настоящее время опыты по дифракции электронов и нейтронов и основанные на них приборы получили широкое распространение в науке и технике. Дифракция электронов применяется при исследовании структуры поверхности. Например, при изучении коррозии, при адсорбции газов на поверхностях.

Метод исследования структуры вещества, основанный на дифракции электронов, получил название электронография. Наличие у электронов заряда вызывает сильное взаимодействие с веществом, благодаря чему проникающая способность электронов намного меньше, чем у рентгеновских лучей. Это обстоятельство делает электронографию особенно ценной при исследовании структур поверхностей. Она позволяет изучать перестройку кристаллической структуры на поверхности и самые начальные стадии кристаллизации твёрдых тел.

Открытие волновых свойств электронов вызвало появление новой отрасли науки, получившей название электронной оптики, и нового прибора – электронного микроскопа. Разрешающая способность любого микроскопа определяется длинной волны применяемого излучения. Использование вместо световых лучей пучков электронов позволяет существенно, в тысячи раз, повысить разрешающую способность микроскопа благодаря чрезвычайно малому значению дебройлевской длины волны электрона. Действительно, для электронов, прошедших ускоряющую разность потенциалов U=10 кВ, длина волны де Бройля составляет =0,0122 нм, что на порядок меньше характерных размеров атомов.

С помощью ускорителей заряженных частиц оказывается возможным получать пучки электронов и протонов очень высоких энергий. В современных ускорителях энергия заряженных частиц может достигать порядка 10 3 ГэВ. Дебройлевская длина волны таких частиц очень мала. Электроны, ускоренные до таких энергий, использовались в экспериментах по изучению размеров и структуры атомных ядер, а также образующих ядра нуклонов – протонов и нейтронов.

В каких случаях волновые свойства играют решающую роль в поведении частицы, а в каких случаях они оказываются несущественными и их можно не учитывать?

Волновые свойства частиц будут наиболее ярко проявляться в тех случаях, когда дебройлевская длина волны частицы сравнима с характерными размерами области движения частицы L. Тоесть, . Например, при взаимодействии электрона с атомами, а так же при их движении в твёрдых телах, волновые свойства электронов будут проявляться максимальным образом, так как дебройлевская длина волны электрона и размеры атома, а также расстояние между атомами в кристалле имеют один и тот же порядок. В тех же случаях, когда длина волны 9.03.2009

Источник

In E n glish

Из проекта Викизнание

Длина волны де Бройля — длина волны, которая проявляется у всех частиц в квантовой механике согласно корпускулярно-волновому дуализму, и определяющая плотность вероятности обнаружения объекта в заданной точке конфигурационного пространства. Длина волны де Бройля обратно пропорциональна импульсу частицы.

Оглавление

Определение

В 1924 году французский физик Луи де Бройль предположил, что для частиц справедливы те же самые соотношения, что и для фотона: [1]

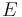
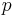
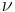
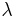
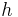
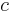
где и – энергия и импульс фотона, и – частота и длина волны фотона, – постоянная Планка, – скорость света.

Отсюда следует определение длины волны де Бройля через постоянную Планка и релятивистский импульс частицы:

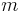
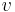
В отличие от фотонов, которые всегда движутся с одной и той же скоростью, равной скорости света, у частиц согласно специальной теории относительности импульсы зависят от массы и от скорости движения по формуле

Вывод формулы для длины волны де Бройля

Существует несколько объяснений тому, что в экспериментах с частицами проявляется длина волны де Бройля. Однако не все эти объяснения могут быть представлены в математической форме, либо они не дают физического механизма, обосновывающего формулу (1).

Волны внутри частиц

При возбуждении одних частиц другими в ходе эксперимента, или при столкновениях частиц с измерительными приборами, в частицах могут возникать внутренние стоячие волны. Это могут быть электромагнитные волны либо волны, связанные с сильным взаимодействием частиц, с сильной гравитацией в гравитационной модели сильного взаимодействия, и т.д. С помощью преобразований Лоренца можно пересчитать длину волны этих внутренних колебаний в длину волны, которую обнаруживает внешний наблюдатель, проводящий эксперимент с движущимися частицами. Расчёт даёт формулу для длины волны де Бройля, [2] [3] [4] а также скорость распространения волны де Бройля:

где 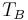– период колебаний волны де Бройля.

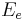
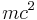
Таким образом, выявляются основные черты, связанные с корпускулярно-волновым дуализмом – если энергия внутренних стоячих волн в частицах достигает энергии покоя этих частиц, то длина волны де Бройля вычисляется так же, как у фотонов при соответствующем импульсе. Если же энергия возбуждения частиц меньше энергии покоя , то длина волны получается по формуле:

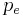
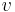
где – импульс той массы-энергии, которая связана с внутренними стоячими волнами, и движется вместе с частицей со скоростью .

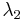
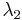
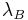
Очевидно, что в экспериментах в основном проявляется длина волны де Бройля (1), как граничная и наименьшая величина для длины волны (2). В то же время эксперименты со множеством частиц могут не дать однозначного значения для длины волны по формуле (2) – если энергии возбуждения частиц не контролируются и различаются у разных частиц, то разброс значений будет слишком велик. Чем выше энергии взаимодействий и энергии возбуждения частиц, тем ближе они будут к энергии покоя и тем ближе будет длина волны к . Лёгкие частицы наподобие электронов быстрее приобретают скорость порядка скорости света, становятся релятивистскими и уже при малых энергиях демонстрируют квантовые и волновые свойства.

Кроме длины волны де Бройля, преобразования Лоренца дают ещё одну длину волны и её период:

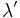
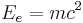
Эта длина волны испытывает лоренцевское сокращение по сравнению с длиной волны в сопутствующей частице системе отсчёта. Кроме этого, эта волна имеет скорость своего распространения, равную скорости движения частицы. В предельном случае, когда энергия возбуждения частиц равна энергии покоя, , для длины волны имеем:

Полученная длина волны есть не что иное, как комптоновская длина волны в эффекте Комптона, с поправкой на фактор Лоренца.

В представленной картине появление волны де Бройля и корпускулярно-волновой дуализм трактуются как чисто релятивистский эффект, возникающий как следствие лоренцевского преобразования стоячей волны, движущейся вместе с частицей. При этом, поскольку длина волны де Бройля ведёт себя подобно длине волны фотона с соответствующим импульсом, что объединяет частицы и волны, волны де Бройля считаются волнами вероятности, связанными с волновой функцией. В квантовой механике принимается, что квадрат амплитуды волновой функции в данной точке в координатном представлении задаёт плотность вероятности обнаружения частицы в этой точке.

У частиц электромагнитный потенциал спадает обратно пропорционально квадрату расстояния от частицы до точки наблюдения, потенциал сильного взаимодействия в гравитационной модели сильного взаимодействия ведёт себя аналогично. При возникновении внутренних колебаний в частице колеблется и потенциал поля вокруг частицы, и следовательно, амплитуда волны де Бройля быстро растёт при приближении к частице. Это как раз соответствует тому, что частица с большей вероятностью находится там, где больше амплитуда её волновой функции. Это верно для чистого состояния, например, для одной частицы. Если же имеется смешанное состояние, когда в учёт берутся волновые функции нескольких взаимодействующих частиц, трактовка, связывающая волновые функции и вероятности становится не такой точной. В этом случае волновая функция скорее будет отражать амплитуду суммарной волны де Бройля, связанную с амплитудой суммарного волнового поля потенциалов частиц.

Преобразования Лоренца для определения длины волны де Бройля были использованы также в статье. [5]

Объяснение волны де Бройля через стоячие волны внутри частиц описывается также в статье. [6] В отличие от этого, в статье [7] предполагается, что внутри частицы имеется круговая электромагнитная волна. Согласно заключению в статье, [8] за пределами движущейся частицы должна быть волна де Бройля с амплитудной модуляцией.

Электроны в атомах

Движение электронов в атомах происходит путём их вращения вокруг атомных ядер. В субстанциональной модели электроны представляют собой облака в форме дисков. Это является результатом действия четырёх приблизительно одинаковых по величине сил, возникающих:

1) от притяжения электрона к ядру за счёт сильной гравитации и кулоновского притяжения зарядов электрона и ядра, 2) от отталкивания заряженного вещества электрона самого от себя, 3) от убегания вещества электрона от ядра за счёт вращения, что учитывается центростремительной силой.

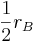
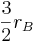
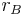
В атоме водорода электрон в состоянии с минимальной энергией может быть моделирован вращающимся диском, внутренний край которого имеет радиус , а внешний край – радиус , где есть боровский радиус. [3]

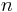
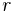
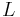
Если предположить, что на орбите электрона в атоме укладывается длин волн де Бройля, то при круговой орбите с радиусом для длины окружности и момента импульса электрона будет следующее:

Это соответствует постулату Боровской модели атома, по которому момент импульса в атоме водорода квантуется и пропорционален номеру орбиты 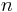и постоянной Планка.

Однако энергия возбуждений в веществе электронов в атомах на стационарных орбитах как правило не равна энергии покоя самих электронов, и потому пространственное квантование волны де Бройля вдоль орбиты в форме (3) следует объяснять другим способом. В частности было показано, что на стационарных орбитах в распредёлённом по пространству веществе электрона осуществляется равенство потока кинетической энергии вещества и суммы потоков энергии от электромагнитного поля и поля сильной гравитации. [3]

В этом случае потоки энергии полей не тормозят и не раскручивают вещество электрона. Это даёт равновесные круговые и эллиптические орбиты электрона в атоме. При этом оказывается, что моменты импульса квантуются пропорционально постоянной Планка, что в первом приближении приводит к соотношению (3).

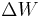
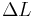
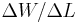
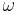
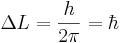
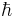
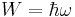
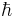
Кроме этого, при переходах с одной орбиты на другую, более близкую к ядру, электроны излучают фотоны, которые уносят из атома энергию и момент импульса . Для фотона корпускулярно-волновой дуализм сводится к прямой связи между этими величинами, а их отношение равно средней угловой частоте волны фотона и одновременно средней угловой скорости электрона , излучающего при соответствующих условиях фотон в атоме при своём вращении. Если полагать, что у каждого фотона , где есть постоянная Дирака, то тогда для энергии фотона имеем: . В таком случае при атомных переходах момент импульса электрона также меняется на , и должна быть справедлива формула (3) для квантования момента импульса в атоме водорода.

При переходе электрона из одного стационарного состояния в другое в его веществе меняются кольцевой поток кинетической энергии и внутренние потоки полей, а также их импульсы и энергии. Синхронно с этим меняется энергия электрона в поле ядра, излучается энергия фотона, увеличивается импульс электрона и уменьшается длина волны де Бройля в (3). Таким образом, излучение фотона как кванта электромагнитного поля из атома сопровождается изменением энергии потоков поля в веществе электрона, оба процесса связаны с энергиями полей и с изменением момента импульса электрона, пропорционального .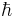

Из соотношения (3) кажется, что на электронной орбите можно расположить 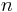длин волн де Бройля. Но при этом энергия возбуждения электрона не достигает энергии его покоя, как это требуется для описания длины волны де Бройля при поступательном движении частиц. Вместо этого возникает связь между моментами импульса и потоками энергии в веществе электрона в стационарных состояниях, и связь при изменении этих моментов импульса и потоков при излучении фотонов.

Другие модели

Ссылки

1. L. de Broglie, Recherches sur la théorie des quanta (Researches on the quantum theory), Thesis (Paris), 1924; L. de Broglie, Ann. Phys . ( Paris ) 3, 22 (1925).

2. Федосин С.Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.

3. Федосин С. Г. Физические теории и бесконечная вложенность материи, Пермь, 2009, 844 стр., Табл. 21, Ил.41, Библ. 289 назв. ISBN 978-5-9901951-1-0.

Источник