проводники в электрическом поле электроемкость конденсаторы

Проводники в электрическом поле. Емкость, конденсаторы. Энергия электрического поля в конденсаторе.

Проводники в электрическом поле. По своим электрическим свойствам все вещества можно разделить на проводники и диэлектрики. В проводниках под действием постоянного электрического поля возникает электрический ток, в диэлектриках – нет. Это объясняется принципиальным различием их структуры. В проводниках существуют носители тока, или свободные заряды, т.е. заряженные частицы, которые под действием поля могут перемещаться в пределах проводника. В диэлектриках таких свободных зарядов нет, все заряженные частицы удерживаются в пределах атомов, молекул, ионов и под действием поля испытывают лишь микроскопические смещения.

Если сообщить проводнику заряд или поместить его во внешнее электростатическое поле, то через достаточно короткий промежуток времени в проводнике установится равновесное распределение заряда, при котором электрический ток отсутствует. Если нейтральный проводник поместить во внешнее электростатическое поле, то в нем произойдет перераспределение зарядов – явление электростатической индукции – т.о., что поле индуцированных зарядов скомпенсирует внешнее поле внутри проводника.

Напряженность на поверхности проводника перпендикулярна этой поверхности, поскольку последняя является эквипотенциальной, причем Е = σ/ε₀.

Электроемкость. Т.к. в условиях электростатического равновесия значения потенциала во всех точках проводника одинаковы, можно говорить, что потенциал φ проводника пропорционален заряду: φ = q/C.

Отношение заряда к потенциалу является для данного проводника постоянной величиной – электрической емкостью проводника: С = q/φ. Емкость зависит от размеров и форм проводника и не зависит от материала, т.к. существует единственное распределение заданного заряда по заданной поверхности, при котором всюду Е = 0. Емкость численно равна заряду, который необходимо сообщить проводнику, чтобы увеличить его потенциал на единицу.

Конденсатор – система, состоящая из 2-х проводников, которым сообщены заряды одинаковой абсолютной величины, но противоположных знаков. Обкладки – проводники в форме тонких пластин той или иной формы. Пространство между ними заполнено диэлектриком.

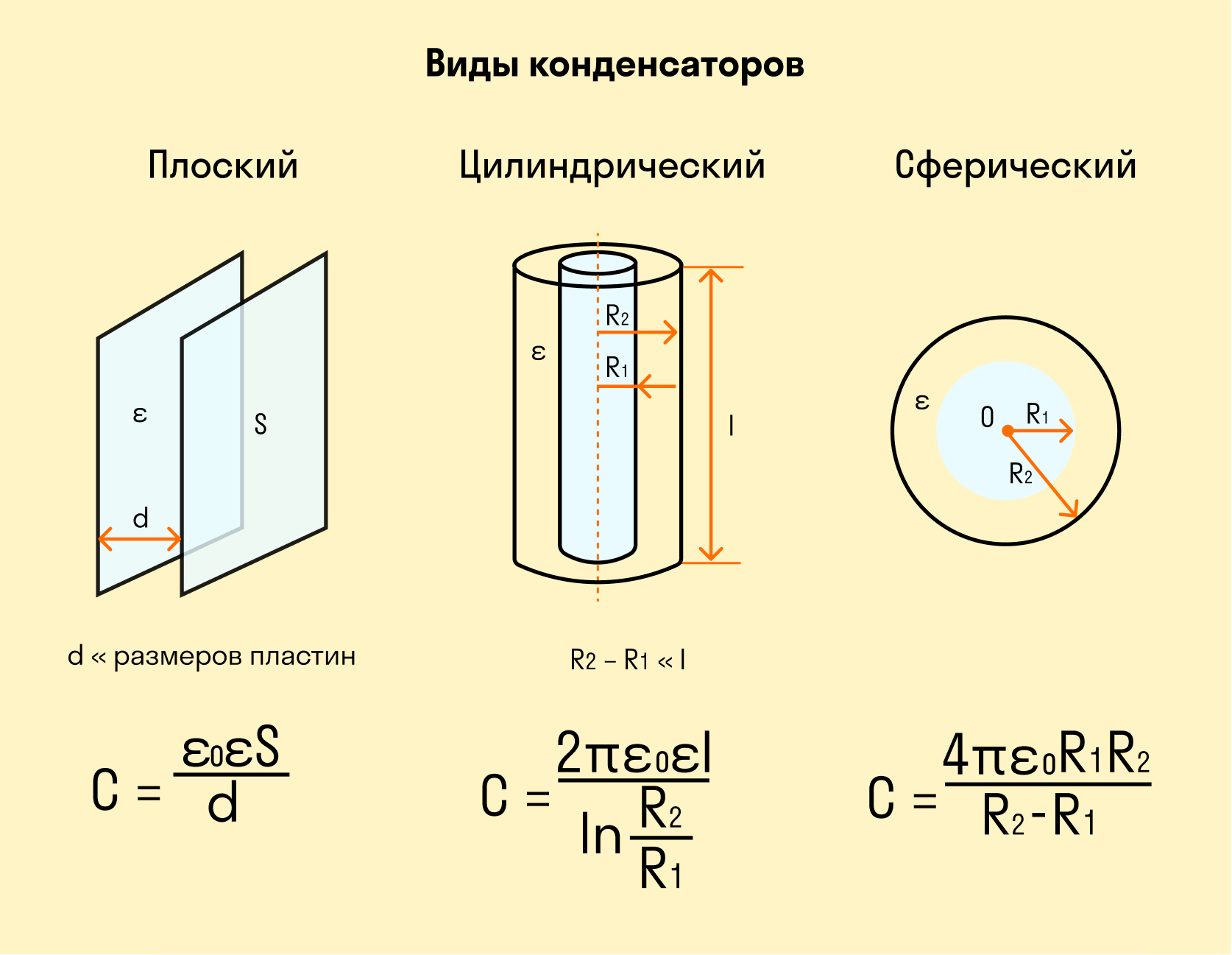
C = q/U – емкость конденсатора. С = ε₀S/d. если пространство между обкладками заполнено однородным диэлектриком с диэлектрической проницаемостью ε, то С = εε₀S/d.

Энергия электрического поля. Энергия заряженного конденсатора – энергия его электрического поля. Для его описания вводится плотность энергии поля – энергия поля в единице объёма: ω=ΔW/ΔV, ΔW – энергия поля в этом объёме ΔV. При пренебрежении краевыми эффектами, электрическое поле конденсатора сосредоточено в пространстве между обкладками и однородно, поэтому плотность энергии одинакова во всех точках между обкладками и равна отношению полной энергии поля к объёму пространства, которое оно занимает: ω = W/V = εε₀E²/2.

По закону сохранения энергии работа, совершенная при разрядке конденсатора, определяет энергию, которой он обладал. Энергия заряженного конденсатора может быть представлена в виде:

W = CU 2 /2 = q 2 /2C = εε₀E²V/2.

5. Постоянный электрический ток. Закон Ома в дифференциальной форме. Электродвижущая сила.

Электрическим током называется упорядоченное движение электрических зарядов.

Условия существования электрического тока:

1) наличие свободных зарядов в проводнике;

2) наличие электрического поля внутри проводника.

Для постоянного тока, т. е. тока, не изменяющегося со временем, справедлива следующая формула: I=q/t.

Напряжением на участке U называется отношение работы электростатических и сторонних сил, действующих на переносимый заряд, к величине этого заряда.

Закон Ома в дифференциальной форме.

Закон Ома в дифференциальной форме справедлив для любой точки участка цепи как с постоянным, так и с переменным сечением. Для однородного участка цепи плотность тока равна

; отсюда: .

Подставим эту формулу, а также формулу для сопротивления (2.26) в закон Ома (2.24)

Учтем, что для однородного поля справедлива формула (2.19)

Тогда

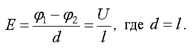
Величина, обратная удельному сопротивлению, называется удельной проводимостью, т. е.

В векторной форме формулу (2.27) можно записать следующим образом

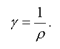
Формула (2.28) выражает закон Ома в дифференциальной форме. Плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление (рис. 2.8).

Рис.2.8

В такой форме закон Ома выражает связь между величинами, относящимися к данной точке, и поэтому применим к неоднородным проводникам.

По аналогии с электрическим полем (см. формулу (2.3)), вводится понятие напряженность поля сторонних сил:

Тогда для любой точки участка цепи, содержащего ЭДС (рис. 2.9), справедлив закон Ома в дифференциальной форме (см. (2.28))

Рис.2.9

Источник

Проводники в электрическом поле. Конденсаторы. Электроемкость

Проводники в электрическом поле. Конденсаторы. Электроемкость

1. Проводники в электростатическом поле.

2. Электроёмкость проводника

3. Конденсаторы. Ёмкость конденсатора

4. Энергия заряженного проводника (конденсатора)

5. Объёмная плотность энергии электростатического поля

1. Проводники в электростатическом поле

Поместим проводник в электростатическое поле (рис.23.1, а). На свободные заряды проводника со стороны поля действует сила, смещающая заряды. Электроны в металле движутся против поля, из точек с меньшим потенциалом в точки с большим потенциалом; тем самым разность потенциалов выравнивается, заряды смещаться перестают. Это равновесное распределение зарядов в проводнике при помещении его в электростатическое поле устанавливается очень быстро, так что в состоянии равновесия разность потенциалов любых двух точек проводника равна нулю. Потенциал проводника всюду (внутри и на поверхности проводника) одинаков:

. (23.1)

Отсюда следует, что электростатического поля внутри проводника нет:

. (23.2)

Внутри проводника нет объёмных нескомпенсированных зарядов; заряды могут быть только на поверхности проводника. Это легко доказать с помощью теоремы Гаусса: если гауссова поверхность целиком лежит внутри проводника, то поток вектора через неё есть ноль, поскольку , значит

.

Поверхность проводника – эквипотенциальная, поэтому линии напряжённости к ней перпендикулярны (рис.23.1, б), а индуцированные на поверхности проводника свободные заряды разрывают линии напряжённости, так что внутри проводника поля нет.

Проводник может быть полым, – это несущественно, всё равно поля внутри объёма, ограниченного проводником, не будет (рис.23.2). На этом и основан принцип экранирования от внешних полей.

Однако если внутри полости поместить заряды, то поле в ней, конечно, будет (рис.23.3). Линии поля разрываются толщей проводника и дальше уходят на бесконечность – поля нет в толще проводника.

Рис.23.4 даёт представление о распределении зарядов, индуцированных на поверхности сферического проводника положительным точечным зарядом. Такое явление называется электростатической индукцией.

Найдём напряжённость поля вблизи поверхности проводника, поверхностная плотность заряда которой равна , по теореме Гаусса для вектора электрического смещения:

.

В качестве гауссовой поверхности возьмём достаточно малый цилиндр, основания которого площадью S параллельны поверхности проводника, а образующие перпендикулярны (рис.23.5). Поток вектора равен нулю как через боковую поверхность (линии к ей параллельны), так и через основание, находящееся в проводнике (там поля нет ). Из-за малости S поток через внешнее основание, перпендикулярное линиям , равен .

Суммарный заряд внутри объёма, ограниченного поверхностью, – это заряд кусочка поверхности площадью S и равен , тогда

. (23.3)

Вблизи поверхности проводника величина вектора равна поверхностной плотности заряда.

. (23.3а)

Одноимённо заряженные участки поверхности проводника отталкиваются. Найдём силу отталкивания, действующую в вакууме на элемент поверхности площадью dS со стороны остальной части поверхности проводника (рис.23.7). Для определённости будем считать, что заряд проводника положительный: .

Пусть – напряжённость поля, созданного зарядом всей поверхности проводника, кроме заряда этого малого участка . Сила, действующая на него со стороны остального заряда проводника, равна

.

Обозначим напряжённость поля, созданного самим зарядом . Вектор направлен от элемента поверхности. Тогда по принципу суперпозиции полное поле . Вне проводника поля и направлены одинаково, и , а внутри – противоположно, то есть .

С другой стороны, вне проводника напряжённость из (23.3а) равна

,

а внутри проводника поля нет:

.

.

2. Электроёмкость проводника

Рассмотрим уединённый заряженный проводник. Как было показано, потенциал любой его точки одинаков. Потенциал проводника прямо пропорционален заряду: , а коэффициент пропорциональности – это ёмкость проводника:

. (23.4)

Электроемкость уединенного проводника показывает, какой заряд нужно сообщить данному проводнику, чтобы его потенциал изменился на единицу. Еди­ни­цей элек­тро­ем­ко­сти в сис­те­ме СИ яв­ля­ет­ся 1 фа­ра­д – это электроем­кость та­ко­го про­вод­ни­ка, по­тен­ци­ал ко­то­ро­го при со­об­щении за­ря­да в 1 ку­лон из­ме­ня­ет­ся на 1 вольт:

.

Найдём ёмкость проводящей сферы радиуса , окружённой безграничной диэлектрической средой. Потенциал поля такой сферы вне сферы ():

.

На поверхности () сферы потенциал равен

,

.

. (23.5)

Электроемкость проводника зависит от его размеров, формы, наличия по соседству других проводников и от диэлектрической проницаемости среды.

Если недалеко от заряженного проводника находится другой проводник, то из-за явления электростатической индукции ёмкость проводника меняется (возрастает): заряды на незаряженном проводнике перераспределяются так, что потенциал неуединённого проводника меньше, чем уединённого. Проще говоря, проводники влияют друг на друга.

3. Конденсаторы. Ёмкость конденсатора

Конденсатор – это два проводника (две обкладки), находящихся вблизи друг друга. Обкладки имеют одинаковые по величине и противоположные по знаку заряды. Взаимная ёмкость (или просто ёмкость) конденсатора определяется формулой (23.6):

, (23.6)

где – разность потенциалов обкладок.

Ёмкость конденсатора численно равна заряду, который нужно ему сообщить, чтобы разность потенциалов обкладок (напряжение на конденсаторе) было равно 1 вольту. Ёмкость зависит от формы, размеров обкладок, их взаимного расположения и диэлектрической проницаемости среды.

Найдём ёмкость плоского конденсатора (рис.23.8,а).

. (23.7)

Для вычисления разности потенциалов на обкладках сферического конденсатора (рис.23.8,б) воспользуемся формулой связи напряженности электростатического поля и потенциала:

.

Интегрировать здесь будем по радиус-вектору, проведенному от внутренней обкладки к внешней (рис.23.9). Вектор напряженности поля направлен радиально (в силу симметрии), тогда

. (23.8)

Напряженность поля между обкладками можно найти по теореме Остроградского-Гаусса, согласно которой поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охваченных поверхностью, деленной на εε0:

. (23.9)

В качестве Гауссовой поверхности в нашем случае следует взять сферу, концентрическую обкладкам, радиусом r: R1

Источник

Электроемкость конденсатора

Электроемкость проводников

Проводники умеют не только проводить через себя электрический ток, но и накапливать заряд. Эта способность характеризуется таким параметром, как электроемкость.

Электроемкость

C = q/φ

С — электроемкость [Ф]

q — электрический заряд [Кл]

φ — потенциал [В]

Особенность этой величины в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости. Самая популярная — формула электроемкости шара.

Электроемкость шара

C = 4πεε₀r

С — электроемкость [Ф]

ε — относительная диэлектрическая проницаемость среды [-]

ε₀ — электрическая постоянная

r — радиус шара [м]

Конденсаторы

Способность накапливать заряд — полезная штука, поэтому люди придумали конденсаторы. Это такие устройства, которые помогают применять электрическую емкость проводников в практических целях.

Конденсатор состоит из двух проводящих пластин (обкладок), разделенных диэлектриком. Между проводящими пластинами образуется электрическое поле, все силовые линии которого идут от одной обкладки к другой.

Когда заряд накапливается на обкладках, происходит процесс под названием зарядка конденсатора. Заряды на разных обкладках равны по величине и противоположны по знаку.

Электроемкость конденсатора измеряется отношением заряда на одной из обкладок к разности потенциалов между обкладками:

Электроемкость конденсатора

C = q/U

С — электроемкость [Ф]

q — электрический заряд [Кл]

U — напряжение (разность потенциалов) [В]

По закону сохранения заряда, если обкладки заряженного конденсатора соединить проводником, то заряды нейтрализуются, переходя с одной обкладки на другую. Так происходит разрядка конденсатора.

Любой конденсатор имеет предел напряжения. Если оно окажется слишком большим, то случится пробой диэлектрика, то есть разрядка произойдет прямо через диэлектрик. Такой конденсатор больше работать не будет.

Виды конденсаторов

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

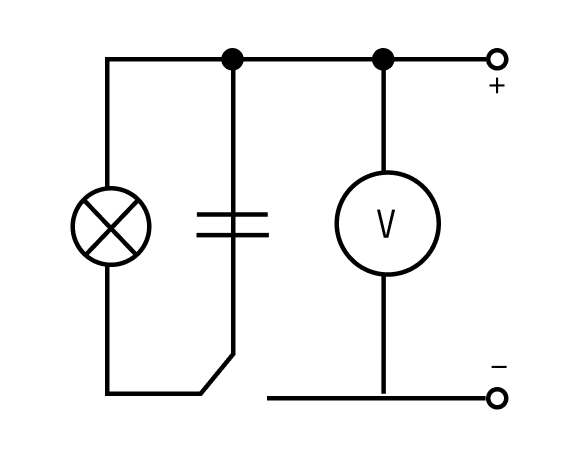
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

Энергия электростатического поля

W_p = qEd

W_p — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

E — напряженность электрического поля [В/м]

d — расстояние от заряда [м]

В случае с конденсатором d будет представлять собой расстояние между пластинами.

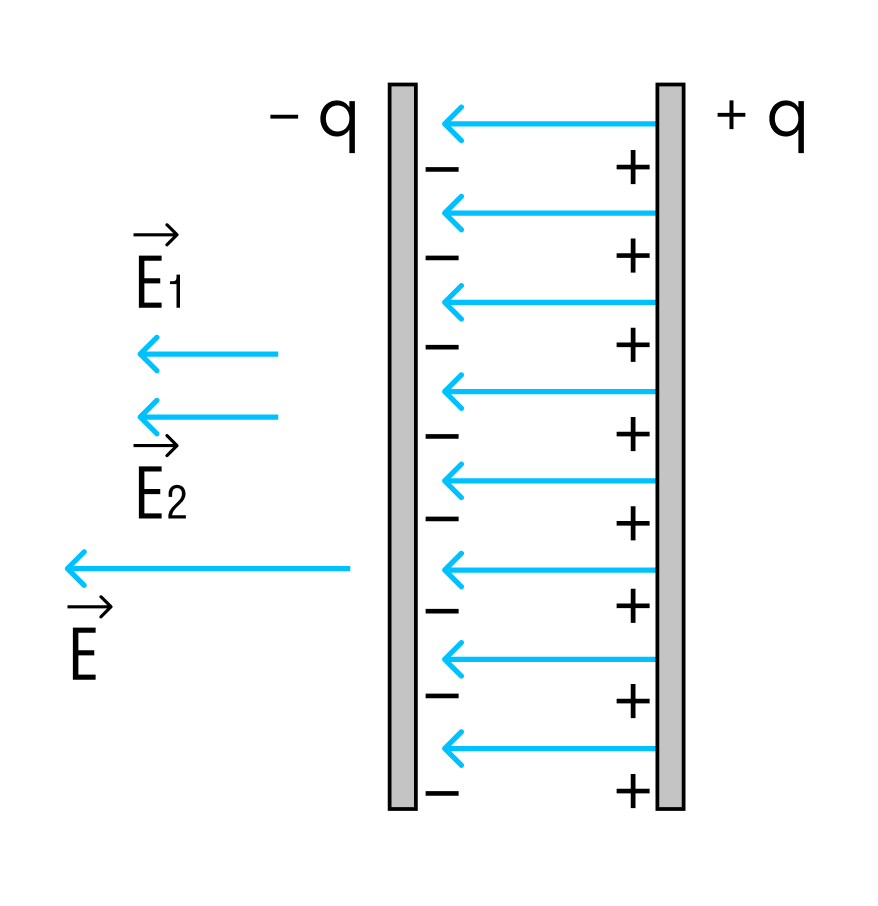
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

Тогда энергия конденсатора равна:

W_p = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

W_p = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора

W_p = qU/2

W_p — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

U — напряжение на конденсаторе [В]

Энергия конденсатора

W_p = q 2 /2C

W_p — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

C — электроемкость конденсатора [Ф]

Энергия конденсатора

W_p = CU 2 /2

W_p — энергия электростатического поля [Дж]

C — электроемкость конденсатора [Ф]

U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Без него не будет работать ни один прибор. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Пример два — тачскрин

Тачскрин на телефоне работает по принципу, схожему с конденсатором. В самом смартфоне, конечно, тоже есть множество конденсаторов, но этот принцип куда интереснее.

Дело в том, что тело человека тоже умеет проводить электричество — у него даже есть сопротивление и электроемкость. Так что можно считать человеческий палец пластиной конденсатора — тело же проводник, почему бы и нет. Но если поднести палец к металлической пластине, получится плохой конденсатор.

В экран телефона встроена матрица из микроскопических пластинок. Когда мы подносим палец к одной из них, получается своего рода конденсатор. Когда перемещаем палец ближе к другой пластинке — еще один конденсатор. Телефон постоянно проверяет пластинки, и если обнаруживает, что у какой-то из них внезапно изменилась электроемкость, значит, рядом есть палец. Координаты пластинки с изменившейся электроемкостью передаются операционной системе телефона, а она уже решает, что с этими координатами делать.

Кстати, то же самое можно проделать, если взять обычную сосиску и поводить ей по экрану смартфона. Тачскрин будет реагировать на все контакты, как реагирует на человеческий палец.

Это не единственный вариант реализации тачскрина, но один из лучших на сегодняшний день. В айфоне используется именно он.

Источник