суждение клиент всегда прав совместимость по истинности с суждением

Суждение клиент всегда прав совместимость по истинности с суждением

В системе гуманитарных наук логике принадлежит особое место. Интерес к ней в настоящее время вызван многими обстоятельствами, и в первую очередь значительным расширением сферы логического знания. Специфической областью его применения является право.

Высокие требования к законотворчеству, правоприменительной практике и правовой теории распространяются также на профессиональное мышление юриста. Поскольку юридическая практика опирается на четкое знание и единообразное применение законов, поскольку она строго регламентирована, постольку необычайную значимость в правовом мышлении приобретает рациональный стиль, правильная оформленность его содержания. Изучение логики способствует достижению этих целей.

Знание логики позволяет юристу точно и аргументированно строить свою речь, видеть несогласованность в показаниях потерпевших, свидетелей, подозреваемых, а также в имеющихся письменных источниках, помогает убедительно опровергать ошибочные доводы оппонентов, правильно составлять план работы, служебные документы, выстраивать следственные версии и т. п.

Главная дидактическая цель пособия состоит в том, чтобы вооружить будущих юристов теоретическими знаниями о формах абстрактного мышления, формально-логических законах, вопросно-ответном комплексе, основах теории аргументации. Учебное пособие включает все основные разделы курса классической логики, определяемые требованиями Государственного образовательного стандарта для юристов.

Очевидно, что изучение логики юристом не может заменить специальных правовых знаний. Однако оно способствует тому, чтобы каждый будущий правовед стал хорошим специалистом в своей области. Недаром известный русский юрист А.Ф. Кони считал, что образованный юрист должен быть человеком, в котором общее образование идет впереди специального. А в системе общего образования одно из ведущих мест принадлежит формально-логической подготовке. Вот почему, по мнению выдающегося отечественного педагога К.Д. Ушинского, логика должна стоять в преддверии всех наук. Развивая способность правильно мыслить, логика дает знания, необходимые для основательного, глубокого усвоения студентами профилирующих юридических учебных дисциплин.

Логика, обладая прикладным характером, позволяет обучаемым освоить теоретически и научиться применять практически логику научного исследования, логику принятия решения (в условиях определенности, неопределенности и риска), логику спора, логику общения, логику конфликтов (межличностных, политических, экономических) и т.д.

При изучении проблем логики важно иметь в виду, что усвоение теоретических вопросов не является самоцелью. Теория — лишь исходное условие и сред­ство, помогающее приобрести навыки правильного рассуждения. Главное — научиться применять приобретенные теоретические знания на практике, в процессе рассуждения. Важную роль в приобретении этих навыков играют специально подобранные практические упражнения. Однако перед выполнением этих упражнений студентам рекомендуется проверить глубину усвоения теоретических проблем, ответив на контрольные вопросы. Определения основных логических терминов, которые даны в словаре, могут быть дополнительно использованы при изучении конкретных вопросов, при решении задач и выполнении упражнений или для предварительного ознакомления при самостоятельной работе.

Проблемы, возникшие в ходе изучения теоретических положений, не поддающиеся решению с помощью средств, изложенных в данном пособии, необходи­мо решать, обращаясь к рекомендуемой дополнительной литературе. Затем следует перейти к выполнению практических упражнений и тестовых заданий, решению занимательных логических задач. В пособии содержится необходимый минимум для активного усвоения теории конкретного вопроса.

Изучение формально-логических проблем требует серьезной и вдумчивой работы. Поэтому глубина проникновения в содержание проблем, последовательность в изучении материала, связь с практикой мышления, решение логических задач, выполнение упражнений и тестовых заданий — непременные условия, которые нужно выполнять не формально, а с пользой для дела.

Учебное пособие предназначено для студентов юридических факультетов вузов. Оно может быть полезно также преподавателям, аспирантам и соискателям юридических кафедр, занимающимся исследованием теоретических проблем права и решением практических юридических вопросов.

Глава 1. ЛОГИКА КАК НАУКА

Освоение проблем формальной логики требует глубокого понимания, в первую очередь, ее объекта и предмета как науки, уяснения методологической роли для конкретного вида деятельности. При этом решаются не только теоретические задачи. Познание предмета логики, истории ее возникновения и развития имеет большое практическое значение, поскольку означает освоение прикладного характера логики, ее нормативных требований, а также превращение их в норму собственной мыслительной деятельности будущих юристов.

§ 1. Мышление как объект логики

Человек, обладая сознанием, отражает действительность, приобретает, знания о природе, обществе и самом себе. Полученные знания сами по себе не имеют самостоятельной ценности. Зна­ние в основном тогда ценно, когда оно позволяет человеку правильно ориентироваться в мире, осуществляя свою жизнедеятельность в нем. Поэтому цель познания заключается в получении не любых знаний, а истинных, использование которых, при соблюдении ряда условий, приводит к верным результатам. Под истиной понимается такое знание, которое адекватно отражает в сознании человека явления и процессы действительности.

Есть знания, истинность которых видна непосредственно. Таковыми, например, являются факты сознания, прямо отражающие последствия совершенного общественно опасного деяния: телесные повреждения потерпевшего, следы действия орудия преступления (царапины на замке, оставленные отмычкой), следы ног или рук преступника, вещественные доказательства (предметы, документы) и т. п. Такого рода факты познаются в процессе непосредственного физического взаимодействия с объектом познания при помощи органов чувств. Эти факты принято называть очевидными, потому что они не нуждаются в доказательстве: их истинность самоочевидна. К числу непосредственно очевидных знаний относятся, прежде всего, те, которые являются результатом чувственного познания. Чувственное познание осуществляется и закрепляется в сознании в трех основных формах: ощущение, восприятие, представление.

Кроме непосредственных знаний, есть знания, истинность которых достигается опосредованно, то есть с помощью других знаний, не всегда обращаясь к показаниям органов чувств. Эти знания являются результатом логического познания, мышления.

Источник

ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ ПО ЗНАЧЕНИЯМ ИСТИННОСТИ

Суждения, как и понятия, делятся на сравнимые (имеют об­щий субъект или предикат) и несравнимые. Сравнимые суждения делятся на совместимые и несовместимые.

Совместимые выражают одну и ту же мысль полностью или лишь в некоторой части. Отношения совместимости: эквивален­тность, логическое подчинение, частичное совпадение (субконтрарность). Совместимые эквивалентные суждения выражают од­ну и ту же мысль в различной форме («Юрий Гагарин — первый космонавт» и «Юрий Гагарин первым полетел в космос»). Субъ­ект здесь один и тот же, а предикаты различные по форме, но одинаковые по смыслу. В двух эквивалентных суждениях: «Миха­ил Шолохов — лауреат Нобелевской премии» и «Автор романа «Тихий Дон» — лауреат Нобелевской премии» — одинаковыми являются предикаты, а различными по форме выражения, но тождественными понятиями — субъекты. Если два высказыва­ния эквивалентны, то невозможно, чтобы одно из них было истинным, а другое ложным.

В сочинении, при заучивании материала, в устном изложении текста, при переводе с одного языка на другой — всюду учащиеся должны уметь кратко и корректно излагать свои мысли. А. П. Чехов дал такое сравнение: «Краткость — сестра таланта».

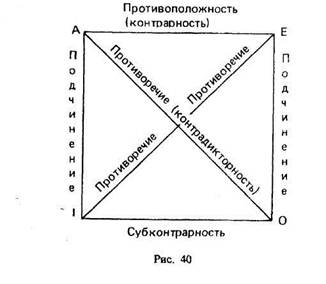
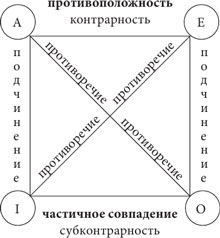
Совместимые суждения, находящиеся в отношении логичес­кого подчинения, имеют общий предикат; понятия, выражающие субъекты двух таких суждений, также находятся в отношении логического подчинения. Отношения между суждениями по ис­тинности принято схематически изображать в виде «Логического квадрата» (рис. 40).

Возьмем суждение «Все учащиеся нашей группы — спортс­мены». Это суждение А общеутвердительное (подчиняющее). Су­ждение I — «Некоторые учащиеся нашей группы — спортсме­ны» — подчиненное.

Для суждении А и I, а также Е и О, находящихся в отношении логического подчинения, истинность общего суждения определя­ет истинность частного, подчиненного суждения. Но ложность общего суждения оставляет частное суждение неопределенным. Истинность частного суждения оставляет общее суждение неоп­ределенным (при нарушении этого правила может возникнуть логическая ошибка — «поспешное обобщение»). Ложность част­ного суждения обусловливает ложность общего суждения. Если истинно суждение «Ни одна трапеция не является сферическим телом», то будет истинным и суждение «Некоторые трапеции не являются сферическими телами». Умозаключение от общего суж­дения к логически подчиненному ему частному суждению всегда будет давать истинное заключение.

В отношении частичного совпадения (субконтрарности) нахо­дятся два таких совместных суждения I и О, которые имеют одинаковые субъекты и одинаковые предикаты, но различаются по качеству. Например, I — «Некоторые свидетели дают истин­ные показания» и О — «Некоторые свидетели не дают истинных показаний». Оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно (оно может быть либо истинным, либо ложным). Например, если истинно суждение I — «Некоторые книги в этой библиотеке — букинистические», то суждение О — «Некоторые книги в этой библиотеке не являются букинистичес­кими» — будет неопределенным, т. е. оно может быть как ис­тинным, так и ложным.

Отношения несовместимости: противоположность, противо­речие. По логическому квадрату в отношении противополож­ности (контрарности) находятся суждения А и Е. Два суждения: А — «Все люди трудятся добросовестно» и Е — «Ни один чело­век не трудится добросовестно» — оба ложны. Но А и Е не могут быть оба истинными. Если одно из противоположных суждений истинно, то другое будет ложным.

Итак, из истинности одного из противоположных суждений вытекает ложность другого, но ложность одного из них оставля­ет другое суждение неопределенным.

В отношении противоречия (контрадикторности) находятся суждения А и О, а также Е и I. Два противоречащих суждения не могут быть одновременно истинными и одновременно ложными. Если в настоящее время истинно суждение I — «Некоторые лет­чики — космонавты», то ложным будет суждение «Ни один лет­чик не является космонавтом».

Закономерности, выражающие отношения между суждениями по истинности, имеют большое познавательное значение, так как они помогают избежать ошибок при непосредственных умозак­лючениях, производимых из одной посылки (одного суждения).

Источник

Логические отношения между суждениями (логический квадрат)

Основу отношений между суждениями составляет их сходство по смыслу и логическим значениям (истинности и ложности). В силу этого отношения устанавливаются не между любыми, а лишь между сравнимыми, т.е. имеющими общий смысл, суждениями.

Несравнимыми среди простых являются суждения, имеющие:

Таковы, например, два суждения:

«Среди космонавтов есть летчики »; «Среди космонавтов есть женщины ».

Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором (суждения одинаковой материи):

Среди сравнимых различают совместимые и несовместимые суждения.

Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемой логическим квадратом.

Логический квадрат

Вершины логического квадрата символизируют простые категорические суждения — А, Е, I, О; стороны и диагонали — отношения между суждениями:

Отношение совместимости

Виды совместимости:

Эквивалентные суждения имеют одинаковые логические характеристики:

С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются.

Различия между высказываниями, содержащими простые эквивалентные суждения, проявляются главным образом словесно.

Например, различными словами могут быть выражены кванторы: «некоторые», «иногда», «как правило» и т.п.; использованы синонимы для выражения субъекта или предиката; суждения могут быть сформулированы на различных национальных языках: «Это стол», «It is a table».

Эту особенность эквивалентных суждений надо учитывать при анализе правовых контекстов, при переводах с одного языка на другой, при сравнении словесно различных утверждений в процессе дискуссии.

Частичная совместимость характерна для суждений I и О, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

При ложности одного из них другое будет истинным. Например, при ложности суждения «Некоторые злаки ядовиты» будет истинным суждение «Некоторые злаки не являются ядовитыми».

В то же время при истинности одного из частных суждений другое может быть как истинным, так и ложным.

Подчинение имеет место между суждениями А и I, E и О. Для них характерны следующие две зависимости:

Например, при истинности общего суждения «Всякое правоотношение регулируется нормами права» истинным будет и частное — «Некоторые правоотношения регулируются нормами права».

При истинности суждения «Ни один кооператив не относится к государственным организациям» будет истинным и суждение «Некоторые кооперативы не относятся к государственным организациям».

Например, если неверно утверждение, что «Некоторые хищения совершаются по неосторожности», то тем более будет неверным утверждение «Всякое хищение совершается по неосторожности».

При подчинении остаются неопределенными следующие зависимости:

Отношение несовместимости

Несовместимыми являются суждения

которые одновременно не могут быть истинными.

Виды несовместимости:

Противоположными (контрарными) являются суждения А и Е, которые одновременно

Истинность одного из противоположных суждений определяет ложность другого. Например, истинность суждения «Все офицеры — военнослужащие» определяет ложность суждения «Ни один офицер не является военнослужащим».

При ложности же одного из противоположных суждений другое остается неопределенным — оно может быть как истинным, так и ложным. Так, например, при ложности суждения «Все птицы улетают зимой в теплые края» ему противоположное «Ни одна птица не улетает зимой в теплые края» тоже оказывается ложным. В другом случае при ложности суждения «Ни один судья не является юристом» ему противоположное «Все судьи — юристы» будет истинным.

Для противоречия характерна строгая, или альтернативная несовместимость:

Отношения между такими суждениями регулируются законом исключенного третьего.

Например, если признается истинным суждение «Все принципиальные люди признают свои ошибки», то ложным будет ему альтернативное: «Некоторые принципиальные люди не признают своих ошибок».

Следует отметить, что несовместимые единичные суждения могут находиться лишь в отношении противоречия и не могут находиться в отношении противоположности, ибо каждому отдельному предмету может быть либо присущ, либо не присущ определенный признак.

Например, суждения «Суд вынес обвинительный приговор по делу Л.» и «Суд не вынес обвинительного приговора по делу Л.» находятся в отношении противоречия: если первое суждение истинно, то признается ложность второго, и наоборот.

Источник

§ 3. отношения между суждениями

§ 3. отношения между суждениями

Устанавливать типы отношений между суждениями важно при сопоставлении разных точек зрения по спорным вопросам, а также и в других случаях.

Основными видами отношений между суждениями по логическим формам являются отношения: совместимости по истинности, совместимости по ложности, логического следования, логической эквивалентности, подчинения, контрадикторности, контрарности, субконтрарности и логической независимости.

Отношение логической совместимости по истинности имеет место между суждениями А и В, если и только если логические формы этих суждений таковы, что существуют суждения этих логических форм (но, возможно, других нелогических содержаний) такие, которые оба являются истинными. Если такие суждения не существуют, то между исходными суждениями имеет место отношение логической несовместимости по истинности.

Отношение логической совместимости по ложности имеет место между суждениями А и В, если и только если существуют суждения А’ и В’, возможно отличающиеся от исходных суждений только нелогическими содержаниями, которые оба являются ложными. Если таковые не существуют, то суждения А и В находятся в отношении логической несовместимости по ложности.

Отношение логического следования имеет место между суждениями А и В (факт наличия этого отношения обозначается так: А |= В или А Þ В), если и только если не существуют суждения А’ и В’ тех же логических форм, что А и В, и, возможно, других нелогических содержаний, такие, что А’ истинно, а В’ ложно.

Отношение логической эквивалентности имеет место между суждениями А и В, если и только если А |= В и В |= А. Оно обозначается так: А Û В.

Суждения А и В находятся в отношении подчинения, если и только если А |= В и В |¹ А. Знак “|¹” означает: “не следует”. Суждение А называется в этом случае подчиняющим, а В — подчиненным.

Отношение противоречия (контрадикторности) имеет место между суждениями, которые несовместимы по истинности и несовместимы по ложности.

Контрарными являются суждения, совместимые по ложности, но несовместимые по истинности.

Субконтрарными являются суждения, которые совместимы по истинности, но несовместимы по ложности.

Суждения являются логически независимыми, если и только если все они совместимы по истинности и ложности и каждое из них не находится в отношении логического следования к другим из этих суждений.

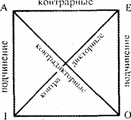
Отношения между атрибутивными суждениями с одними и теми же терминами изображаются посредством схемы, называемой логическим квадратом:

Между суждениями форм А и I, а также форм Е и О имеет место отношение подчинения. Между А и Е — контрарности, а I и О — субконтрарности. Суждения логических форм А и О, а также Е и I находятся в отношении контрадикторности.

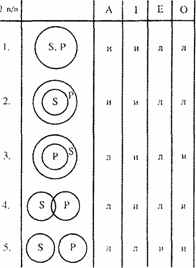
Устанавливать отношения между суждениями можно также с помощью следующей таблицы:

В ней указаны возможные значения истинности суждений различных видов при различных отношениях между объемами их терминов ( S и P). Например, нет строк, в которых суждения форм А и О оба имеют значение “истина”, нет таких строк, в которых оба имеют значение “ложь”. Следовательно, суждения А и О находятся в отношении контрадикторности.

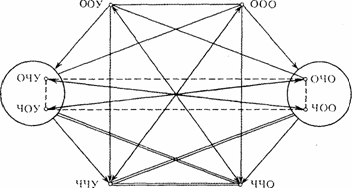
Отношения между суждениями о двухместных отношениях можно изобразить при помощи логического квазишестиугольника:

Сокращенно суждения о двухместных отношениях обозначаются словами, состоящими из заглавных букв О (общее), Ч (частное), У (утвердительное), О (отрицательное). В последнем смысле буква О понимается лишь тогда, когда она находится в конце трехбуквенного слова. Например, слово «ООО» обозначает обще-общеотрицательное суждение, слово » ЧОУ» — частно-общеутвердительное суждение и т.д.

На схеме двойной стрелкой изображено отношение контрадикторности, стрелкой — отношение подчинения, прямой — отношение контрарности, двойной линией — субконтрарности, штриховой — отношение логической независимости.

Методы установления отношений между сложными суждениями излагаются в главе V.

В каком отношении находятся суждения?

1. Если идет дождь, то крыши мокрые. Дождя нет, а крыши мокрые.

2. Некоторые юристы обладают ораторскими способностями. Некоторые юристы не обладают ораторскими способностями.

3. Если тело является кристаллическим, то оно имеет определенную температуру плавления. Данное тело не является кристаллическим, поскольку оно не имеет определенной температуры плавления.

4. Если подсудимый виновен, то у него был сообщник. Подсудимый виновен, но у него не было сообщника.

5. Если болезнь запущена, то ее легко распознать, но трудно излечить. Если болезнь не запущена, то ее трудно распознать, но легко излечить.

6. Тому, кто тратит свое, лучше всего быть бережливым. Тому, кто тратит чужое, можно быть щедрым.

7. Если человек совершил преступление и это установлено, то он подлежит привлечению к уголовной ответственности. Если человек совершил преступление, то он подлежит привлечению к уголовной ответственности. Человек совершил преступление, но не подлежит привлечению к уголовной ответственности.

Источник

9. Краткий курс классической логики. Суждение

Суждение – это форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: «Некоторые студенты – отличники», «Все люди – смертные».
Суждения составляется из понятий, оно предоставляет собой чаще всего повествовательное предложение. В редких случаях оно бывает риторическое-восклицательное или риторическое-вопросительное предложение, которое что-то утверждает или отрицает.
Бывают простые и сложные суждения, сложные суждения складываются из двух или более простых суждений соединённых союзом.
Суждение на отмену от понятий бывают истинные и ложные, а так же имеют сложную структуру, которая складывается из таких понятий:

Субъект и предикат суждения могут состоять в отношениях:
1.Равнозначности – когда объем субъекта равен объёму предиката. «Все квадраты – равносторонние прямоугольники».
2.Подчинения – когда объем субъекта входит в объем предиката или наоборот. «Все березы – это деревья». Объем понятия деревья больше понятия березы, так как береза только одно из разновидностей деревьев.
3.Пересечения – когда объемы субъекта и предиката пересекаются частично, к примеру, «Некоторые литераторы – это лауреаты нобелевской премии». Литераторы могут быть лауреатами нобелевской премии, но могут и не быть, так же как и лауреаты нобелевской премии могут быть литераторами, но могут ими и не быть. Объем этих понятий совпадает только в некоторых случаях, потому субъект и предикат находятся в отношении пересечения.
4.Несовместимости – когда объемы субъекта и предиката не имеют общих точек соприкосновения. «Звезды – это не планеты». Чаще субъект и предикат, входя в третье более общее понятия, в нашем случае – это небесные тела.

Важно заметить, что при обращении, суждения меняют свой тип, согласно ниже приведенных примеров:
Суждения типа А:
равнозначности – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа I:
пересечения – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа Е:
несовместимости – обращается в самое себя.
Суждения типа О:
пересечения – обращению не поддается.
подчинения – обращению не поддаётся.

Второе действие над суждениями — превращения. Оно заключается в том, что у суждения меняется связка, положительная на отрицательную или наоборот. При этом предикат суждения меняется на противоречащий, перед ним ставиться частица «не». Вернемся к нашему исходному суждению: «Все акулы – являются рыбами». Результатом превращения будет суждения: «Все акулы не являются не рыбами». Выглядит это суждения непривычно, однако это более короткое изречение той мысли, что если какое-то животное не являются акулой, то оно не являются и рыбой. Или, что если какое-то животное является акулой то оно обязательно должно являться рыбой, ни одна акула не может быть таким существом, которое бы не являлось при этом рыбой.

В отличие от обращения превращение не зависит от характера отношения субъекта и предиката простого суждения:
Суждения типа А всегда превращается в суждения типа Е, и наоборот.
Суждения типа I всегда превращается в суждения типа О, и наоборот.

При действии противоставления предикату суждения меняют свой тип, аналогично обращении.

В итоге, из одного суждения, мы можем получить четыре:
1. Исходное суждение: «Все акулы являются рыбами».
2. Результат обращения: «Некоторые рыбы – это акулы».
3. Результат превращения: «Все акулы не являются не рыбами».
4. Результат противоставления предикату: «Все не рыбы не являются акулами».

Если мы разобрались с этим, то совершить превращения и противоставления предикату этого суждения совсем не проблематично. Получиться, как и в первом варианте — четыре суждения:

Исходное суждение: «Идти назад – значит не идти вперед»
Обращения: «Иногда не идти вперед, значит идти назад».
Превращения: «Идти назад не означает, не идти вперед».
Противоставление предикату: «Иногда не идти вперед не означает, не идти назад».

Несовместимые суждения находятся в отношениях:
Противоположности (контарность) – суждения, в которых, так же как при отношении частичного совпадения, субъект и предикат совпадает, а связка отличается, но в этом случае суждения могут быть только общими: общеутвердительными (А) или общеотрицательными (О). «Все люди – лгут», «Все люди – не лгут». Важным признаком противоположных суждений является то, что они не могут быть одновременно истинные как несовместимые, но при этом могут быть одновременно ложными. Между этими суждениями всегда можно вставить третье, нейтральное утверждение. В нашем примере это «Некоторые люди лгут, а некоторые не лгут». Это суждение, будучи истинным, доказывает ложность двух первых.
Противоречия (контрадикторность) – это отношения между двумя суждениями в которых предикаты совпадают, связки отличаются, а субъекты находятся в родовом, видовом отношении, то есть отличаются объемами. «Все люди – являются разумными существами», Некоторые люди – не являются разумными существами». На отмену от противоположных суждений противоречивые, не могу быть одновременно ложными. Ложность одного непременно будет доказательством истинности другого, и наоборот.
Возможные отношения между простыми суждениями отображают посредством, так называемого логического квадрата:

Истинное значение суждения, связано с истинностью значений всех других сравнимых суждений. К примеру если суждения типа А: «Все акулы – являются рыбами» истинно, смотря на логический квадрат, можно определить, что суждения типа I: «Некоторые рыбы – являются акулами», тоже будет истинным. Суждения типа Е: «Все акулы – не являются рыбами», точно так же как и суждения типа О: «Некоторые акулы – не являются рыбами», будут ложными.

Еще несколько слов о сложных суждениях. В зависимости от союза, которым соединяются простые суждения в сложные, выделяют пять видов сложного суждения:

Источник